50 bài tập trắc nghiệm hệ tọa độ trong không gian mức độ nhận biếtLàm bàiCâu hỏi 1 : Trong không gian với hệ tọa độ \(Oxyz,\) tam giác \(ABC\) có \(A\left( -\,1;-\,2;4 \right),\,\,B\left( -\,4;-\,2;0 \right)\) và \(C\left( 3;-\,2;1 \right).\) Tính số đo của góc \(B.\)
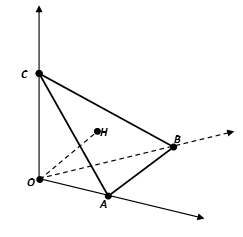
Đáp án: A Phương pháp giải: Tính độ dài các cạnh của tam giác và nhận xét sự đặc biệt của tam giác đó. Lời giải chi tiết: Ta có \(AB=5,\,\,AC=5\) và \(BC=5\sqrt{2}\)\(\Rightarrow \,\,A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}}\) Suy ra tam giác \(ABC\) vuông cân tại \(A\,\,\Rightarrow \,\,\widehat{ABC}={{45}^{0}}.\) Chọn A. Câu hỏi 2 : Trong không gian với hệ trục tọa độ \(Oxyz\), cho \(H\left( 1;\text{1};-3 \right)\). Phương trình mặt phẳng \(\left( P \right)\) đi qua \(H\) cắt các trục tọa độ \(Ox\), \(Oy\), \(Oz\) lần lượt tại \(A\), \(B\), \(C\) (khác \(O\)) sao cho \(H\) là trực tâm tam giác \(ABC\) là
Đáp án: C Phương pháp giải: Với tam diện vuông \(O.ABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc và \(H\) là trực tâm của tam giác \(ABC\) thì \(OH\) vuông góc với mặt phẳng \(\left( ABC \right)\) Lời giải chi tiết: Hình vẽ tham khảo Do \(H\) là trực tâm \(\Delta ABC\Rightarrow AH\bot BC\). Mặt khác \(OA\bot \left( OBC \right)\)\(\Rightarrow OA\bot BC\)\(\Rightarrow BC\bot \left( OAH \right)\)\(\Rightarrow OH\bot BC\). Tương tự: \(OH\bot AB\)\(\Rightarrow OH\bot \left( ABC \right)\) hay \(\overrightarrow{OH}=\left( 1;1;-3 \right)\) là vectơ pháp tuyến của mặt phẳng \(\left( P \right)\). Hơn nữa, \(\left( P \right)\) đi qua \(H\left( 1;1;-3 \right)\) nên phương trình mặt phẳng \(\left( P \right)\) là \(x+y-3z-11=0\). Chọn C Câu hỏi 3 : Trong không gian với hệ tọa độ Oxyz, cho ba điểm \(A\left( {1;0;0} \right)\), \(B\left( {0;1;0} \right)\), \(C\left( {0;0; - 2} \right)\). Vectơ nào dưới đây là vectơ pháp tuyến của mặt phẳng (ABC)?
Đáp án: A Phương pháp giải: Sử dụng phương trình theo đoạn chắn của mặt phẳng. Lời giải chi tiết: Mặt phẳng (ABC) cắt các trục tọa độ Ox, Oy, Oz lần lượt tại \(A\left( {1;0;0} \right)\), \(B\left( {0;1;0} \right)\), \(C\left( {0;0; - 2} \right)\)
\( \Rightarrow \left( {ABC} \right):\,\,\dfrac{x}{1} + \dfrac{y}{1} + \dfrac{z}{{ - 2}} = 1 \Leftrightarrow 2x + 2y - z + 2 = 0\)\( \Rightarrow \left( {ABC} \right)\) nhận vectơ \(\overrightarrow n = \left( {2;2; - 1} \right)\) làm VTPT. Chọn: A
Câu hỏi 4 : Trong không gian với hệ tọa độ Oxyz, cho vectơ \(\overrightarrow a = \left( {1; - 2;3} \right)\). Tìm tọa độ của vectơ \(\overrightarrow b \), biết rằng \(\overrightarrow b \) ngược hướng với \(\overrightarrow a \) và \(\left| {\overrightarrow b } \right| = 2\left| {\overrightarrow a } \right|\).
Đáp án: D Phương pháp giải: \(\overrightarrow b \) ngược hướng với \(\overrightarrow a \) và \(\left| {\overrightarrow b } \right| = k\left| {\overrightarrow a } \right| \Rightarrow \overrightarrow b = - k\overrightarrow a \) Lời giải chi tiết: Cách giải: \(\overrightarrow b \) ngược hướng với \(\overrightarrow a \) và \(\left| {\overrightarrow b } \right| = 2\left| {\overrightarrow a } \right|\) \( \Leftrightarrow \overrightarrow b = - 2\overrightarrow a \,\, \Rightarrow \)\(\overrightarrow b = \left( { - 2;4; - 6} \right)\). Chọn: D Câu hỏi 5 : Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {1;3;2} \right),\,\,B\left( {2; - 1;5} \right),\,\,C\left( {3;2; - 1} \right)\). Tìm tọa độ điểm \(D\) sao cho \(ABCD\) là hình bình hành.
Đáp án: C Phương pháp giải: \(ABCD\) là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \). Lời giải chi tiết: Gọi \(D\left( {a;b;c} \right)\). \(ABCD\) là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \). \( \Leftrightarrow \left( {1; - 4;3} \right) = \left( {3 - a;2 - b; - 1 - c} \right) \Leftrightarrow \left\{ \begin{array}{l}1 = 3 - a\\ - 4 = 2 - b\\3 = - 1 - c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 6\\c = - 4\end{array} \right. \Rightarrow D\left( {2;6; - 4} \right)\). Chọn C Câu hỏi 6 : Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {1;3;2} \right),\,\,B\left( {2; - 1;5} \right)\) và \(C\left( {3;2; - 1} \right)\). Gọi \(\overrightarrow n = \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right]\) là tích có hướng của hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \). Tìm tọa độ vectơ \(\overrightarrow n \).
Đáp án: A Phương pháp giải: Cho hai vectơ \(\overrightarrow a = \left( {{a_1};{a_2};{a_3}} \right),\,\,\overrightarrow b = \left( {{b_1};{b_2};{b_3}} \right)\). Khi đó: \(\left[ {\overrightarrow a ;\overrightarrow b } \right] = \left( {\left| {\begin{array}{*{20}{c}}{{a_2}}&{{a_3}}\\{{b_2}}&{{b_3}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{a_3}}&{{a_1}}\\{{b_3}}&{{b_1}}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|} \right)\). Lời giải chi tiết: Ta có: \(\overrightarrow {AB} = \left( {1; - 4;3} \right),\,\,\overrightarrow {AC} = \left( {2; - 1; - 3} \right)\)\( \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( {15;9;7} \right)\). Chọn A Câu hỏi 7 : Trong không gian với hệ trục tọa độ Oxyz, cho \(\overrightarrow u = \left( { - 2;3;0} \right),\overrightarrow v = \left( {2; - 2;1} \right)\). Độ dài của vectơ \(\overrightarrow {\bf{w}} = \overrightarrow u - 2\overrightarrow v \) là
Đáp án: C Phương pháp giải: \(\overrightarrow u = \left( {a;b;c} \right) \Rightarrow \left| {\overrightarrow u } \right| = \sqrt {{a^2} + {b^2} + {c^2}} \) Lời giải chi tiết: \(\overrightarrow u = \left( { - 2;3;0} \right),\overrightarrow v = \left( {2; - 2;1} \right)\)\( \Rightarrow \overrightarrow {\bf{w}} = \overrightarrow u - 2\overrightarrow v = \left( { - 6;7; - 2} \right) \Rightarrow \left| {\overrightarrow {\bf{w}} } \right| = \sqrt {{6^2} + {7^2} + {2^2}} = \sqrt {89} \). Chọn: C Câu hỏi 8 : Trong không gian \(Oxyz,\)cho vectơ \(\overrightarrow {OA} = \overrightarrow j - 2\overrightarrow k .\) Tọa độ điểm \(A\) là
Đáp án: A Phương pháp giải: Véc tơ \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \) thì \(M\left( {x;y;z} \right)\). Lời giải chi tiết: Ta có : \(\overrightarrow {OA} = \overrightarrow j - 2\overrightarrow k = 0.\overrightarrow i + 1.\overrightarrow j - 2.\overrightarrow k \Rightarrow A\left( {0;1; - 2} \right)\). Chọn A. Câu hỏi 9 : Trong không gian với hệ tọa độ Oxyz, cho \(A\left( {4;0;2} \right),B\left( {0;2;0} \right)\), \(M\) là điểm thỏa mãn \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \), tọa độ của điểm \(M\) là:
Đáp án: D Phương pháp giải: \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow M\) là trung điểm của AB. Lời giải chi tiết: \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow M\) là trung điểm của AB \( \Leftrightarrow \)\(M\left( {2;1;1} \right)\). Chọn: D Câu hỏi 10 : Trong không gian với hệ tọa độ Oxyz, cho vectơ \(\overrightarrow u = \left( {1;2;{{\log }_2}3} \right),\overrightarrow v = \left( {2; - 2;{{\log }_3}2} \right)\). Khi đó, tích vô hướng \(\overrightarrow u .\overrightarrow v \) được xác định:
Đáp án: B Phương pháp giải: \(\overrightarrow u = \left( {{a_1};{b_1};{c_1}} \right);\,\,\overrightarrow v = \left( {{a_2};{b_2};{c_2}} \right) \Rightarrow \overrightarrow u .\overrightarrow v = {a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}\). Lời giải chi tiết: \(\overrightarrow u .\overrightarrow v = 1.2 + 2.\left( { - 2} \right) + {\log _2}3.{\log _3}2 = 2 - 4 + 1 = - 1\). Chọn: B Câu hỏi 11 : Trong không gian với hệ tọa độ Oxyz, cho điểm \(M\left( {1; - 2; - 3} \right)\). Tọa độ điểm M’ đối xứng với điểm M qua mặt phẳng \(\left( {Oxz} \right)\) là:
Đáp án: A Phương pháp giải: M’ đối xứng với điểm \(M\left( {x;y;z} \right)\) qua mặt phẳng \(\left( {Oxz} \right)\)\( \Rightarrow M'\left( {x; - y;z} \right)\) Lời giải chi tiết: Tọa độ điểm M’ đối xứng với điểm \(M\left( {1; - 2; - 3} \right)\) qua mặt phẳng \(\left( {Oxz} \right)\) là: \(M'\left( {1;2; - 3} \right)\). Chọn: A Câu hỏi 12 : Trong không gian \(Oxyz\), cho hai điểm \(A\left( { - 2;4;1} \right)\) và \(B\left( {4;5;2} \right)\). Điểm \(C\) thỏa mãn \(\overrightarrow {OC} = \overrightarrow {BA} \) có tọa độ là
Đáp án: A Phương pháp giải: Hai véc tơ \(\overrightarrow a = \left( {x;y;z} \right)\) và \(\overrightarrow {a'} = \left( {x';y';z'} \right)\) bằng nhau nếu \(\left\{ \begin{array}{l}a = a'\\b = b'\\c = c'\end{array} \right.\) Lời giải chi tiết: Gọi tọa độ điểm \(C\left( {x;y;z} \right)\) ta có \(\overrightarrow {OC} = \left( {x;y;z} \right),\overrightarrow {BA} = \left( { - 6; - 1; - 1} \right)\). \(\overrightarrow {OC} = \overrightarrow {BA} \Leftrightarrow \left\{ \begin{array}{l}x = - 6\\y = - 1\\z = - 1\end{array} \right. \Rightarrow C\left( { - 6; - 1; - 1} \right)\). Chọn A. Câu hỏi 13 : Trong không gian \(Oxyz,\) cho hai điểm \(A\left( { - 2; - 1;\,\,3} \right)\) và \(B\left( {0;\,\,3;\,\,1} \right).\) Gọi \(\left( \alpha \right)\) là mặt phẳng trung trực của \(AB.\) Một vecto pháp tuyến của \(\left( \alpha \right)\) có tọa độ là:
Đáp án: B Phương pháp giải: Mặt phẳng trung trực \(\left( \alpha \right)\) của đoạn thẳng \(AB\) nhận \(\overrightarrow {AB} \) làm một VTPT. Lời giải chi tiết: Mặt phẳng trung trực \(\left( \alpha \right)\) của đoạn thẳng \(AB\) nhận \(\overrightarrow {AB} \) làm một VTPT. Ta có: \(\overrightarrow {AB} = \left( {2;\,\,4;\,\, - 2} \right) = 2\left( {1;\,2; - 1} \right)//\,\,\left( {1;\,\,2; - 1} \right)\) \( \Rightarrow \left( \alpha \right)\) nhận vecto \(\left( {1;\,2; - 1} \right)\) làm 1 VTPT. Chọn B. Câu hỏi 14 : Trong không gian tọa độ \(Oxyz,\) góc giữa hai véc tơ \(\overrightarrow i \) và \(\overrightarrow u = ( - \sqrt 3 ;0;1)\)là
Đáp án: D Phương pháp giải: Lời giải chi tiết: Chọn D. Câu hỏi 15 : Trong không gian với hệ tọa độ \(Oxyz\), tìm \(m,\,\,n\) sao cho vectơ \(\overrightarrow a = \left( {1;1; - 2} \right),\,\,\overrightarrow b = \left( {2;m;n} \right)\) cùng phương.
Đáp án: D Phương pháp giải: \(\overrightarrow a ,\,\,\overrightarrow b \) được gọi là cùng phương \( \Leftrightarrow \exists k \ne 0:\,\,\overrightarrow a = k\overrightarrow b \). Lời giải chi tiết: \(\overrightarrow a ;\,\overrightarrow b \) cùng phương \( \Leftrightarrow \dfrac{2}{1} = \dfrac{m}{1} = \dfrac{n}{{ - 2}} \Leftrightarrow \left\{ \begin{array}{l}m = 2\\n = - 4\end{array} \right.\). Chọn D. Câu hỏi 16 : Trong không gian với hệ tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j ;\overrightarrow k } \right)\), cho \(\overrightarrow u = 2\overrightarrow i - \overrightarrow j + \overrightarrow k \). Tính \(\left| {\overrightarrow u } \right|\)?
Đáp án: A Phương pháp giải: Với \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j + c\overrightarrow k \Rightarrow \overrightarrow u = \left( {a;b;c} \right) \Rightarrow \left| {\overrightarrow u } \right| = \sqrt {{a^2} + {b^2} + {c^2}} \). Lời giải chi tiết: \(\overrightarrow u = 2\overrightarrow i - \overrightarrow j + \overrightarrow k \Rightarrow \overrightarrow u \left( {2; - 1;1} \right) \Rightarrow \left| {\overrightarrow u } \right| = \sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {1^2}} = \sqrt 6 \) Chọn A Câu hỏi 17 : Trong không gian \(Oxyz,\) hình chiếu của điểm \(M(1;2;3)\) trên mặt phẳng \((Oxy)\) có tọa độ là
Đáp án: A Phương pháp giải: Hình chiếu của \(M\left( {a;b;c} \right)\) lên mặt phẳng \(\left( {Oxy} \right)\) là \(H\left( {a;b;0} \right)\) Lời giải chi tiết: Hình chiếu của \(M\left( {1;2;3} \right)\) lên mặt phẳng \(\left( {Oxy} \right)\) là \(H\left( {1;2;0} \right)\) Chọn A. Câu hỏi 18 : Trong không gian \(Oxyz\), cho điểm \(M\) thỏa mãn hệ thức \(\overrightarrow {OM} = 2\overrightarrow i + \overrightarrow j \). Tọa độ của điểm \(M\) là
Đáp án: B Phương pháp giải: Điểm \(M\left( {x;y;z} \right)\) nếu \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \). Lời giải chi tiết: Ta có: \(\overrightarrow {OM} = 2\overrightarrow i + \overrightarrow j \) nên \(M\left( {2;1;0} \right)\). Chọn B. Câu hỏi 19 : Trong không gian \(Oxyz\), cho hai véc tơ \(\overrightarrow a = \left( { - 4;5; - 3} \right)\) và \(\overrightarrow b = \left( {2; - 2;3} \right)\). Véc tơ \(\overrightarrow x = \overrightarrow a + 2\overrightarrow b \) có tọa độ là
Đáp án: C Phương pháp giải: Lời giải chi tiết: Chọn C. Câu hỏi 20 : Trong không gian \(Oxyz\), cho 2 điểm \(M(2; - 4;1)\,;N(3;0; - 1)\). Tọa độ véctơ \(\overrightarrow {MN} \) là:
Đáp án: A Phương pháp giải: \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\). Lời giải chi tiết: \(M\left( {2; - 4;1} \right)\,;N\left( {3;0; - 1} \right) \Rightarrow \overrightarrow {MN} = \left( {1;4; - 2} \right)\). Chọn: A Câu hỏi 21 : Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( \alpha \right)\) có phương trình: \(2x + 3y - 3z + 4 = 0.\) Điểm nào sau đây thuộc mặt phẳng \(\left( \alpha \right)?\)
Đáp án: D Phương pháp giải: Thay tọa độ các điểm \(M,\,\,N,\,\,P,\,\,Q\) vào phương trình mặt phẳng \(\left( \alpha \right),\) tọa độ điểm nào thỏa mãn phương trình thì chọn đáp án đó. Lời giải chi tiết: +) Xét điểm \(Q\left( {2; - 1; - 1} \right)\) ta có: \(2.2 + 3.\left( { - 1} \right) - 3\left( { - 1} \right) + 4 = 8 \ne 0 \Rightarrow Q \notin \left( \alpha \right).\) +) Xét điểm \(N\left( {1;\,\,1;\,\,1} \right)\) ta có: \(2.1 + 3.1 - 3.1 + 4 = 6 \ne 0 \Rightarrow N \notin \left( \alpha \right).\) +) Xét điểm \(P\left( {2;\,\,1;\,\,1} \right)\) ta có: \(2.2 + 3.1 - 3.1 + 4 = 8 \ne 0 \Rightarrow P \notin \left( \alpha \right).\) +) Xét điểm \(M\left( { - 2;\,\,1;\,\,1} \right)\) ta có: \(2.\left( { - 2} \right) + 3.1 - 3.1 + 4 = 0 \Rightarrow M \in \left( \alpha \right).\) Chọn D. Câu hỏi 22 : Trong không gian \(Oxyz\) cho ba vecto \(\overrightarrow a = \left( { - 1;1;0} \right);\)\(\overrightarrow b = \left( {2;2;0} \right);\)\(\overrightarrow c = \left( {1;1;1} \right)\). Trong các khẳng định sau khẳng định nào sai?
Đáp án: D Phương pháp giải: Sử dụng các công thức: - Tích vô hướng: \(\overrightarrow a \left( {{x_1};{y_1};{z_2}} \right);\,\,\overrightarrow b \left( {{x_2};{y_2};{z_2}} \right)\) \( \Rightarrow \overrightarrow a .\overrightarrow b = {x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}\). - Độ dài vectơ: \(\overrightarrow a \left( {x;y;z} \right)\) \( \Rightarrow \left| {\overrightarrow a } \right| = \sqrt {{x^2} + {y^2} + {z^2}} \). Hai vectơ vuông góc với nhau khi và chỉ khi tích vô hướng của chúng bằng 0. Lời giải chi tiết: Ta có \(\overrightarrow b \left( {2;2;0} \right);\overrightarrow c \left( {1;1;1} \right)\)\( \Rightarrow \overrightarrow b .\overrightarrow c = 2.1 + 2.1 + 0.1 = 4 \ne 0.\) Suy ra \(\overrightarrow b \) không vuông góc với \(\overrightarrow c \), do đó khẳng định D sai. Chọn D. Câu hỏi 23 : Trong hệ tọa độ \(Oxyz\), cho \(\overrightarrow a \left( {1;m;-1} \right)\)và \(\overrightarrow b \left( {2;1;3} \right)\). Tìm giá trị của \(m\) để \(\overrightarrow a \bot \overrightarrow b \).
Đáp án: D Phương pháp giải: \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\) Lời giải chi tiết: \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0 \Leftrightarrow 2 + m - 3 = 0 \Leftrightarrow m = 1.\) Chọn D. Câu hỏi 24 : Trong không gian \(Oxyz\), độ dài của vecto \(\overrightarrow u = \left( { - 3;4;0} \right)\) bằng
Đáp án: D Phương pháp giải: Áp dụng công thức tính độ dài vecto: \(\overrightarrow u \left( {a;b;c} \right) \Rightarrow \left| {\overrightarrow u } \right| = \sqrt {{a^2} + {b^2} + {c^2}} \). Lời giải chi tiết: \(\left| {\overrightarrow u } \right| = \sqrt {{{\left( { - 3} \right)}^2} + {4^2} + {0^2}} = \sqrt {25} = 5.\) Chọn D. Câu hỏi 25 : Trong không gian \(Oxyz\), cho điểm \(M\) thỏa mãn \(\overrightarrow {OM} = - 4\overrightarrow i + 5\overrightarrow k \). Khi đó, tọa độ của điểm \(M\) là
Đáp án: A Phương pháp giải: Điểm \(M\) thỏa mãn \(\overrightarrow {OM} = a\overrightarrow i + b\overrightarrow j + c\overrightarrow z \) có tọa độ \(M\left( {a;b;c} \right)\). Lời giải chi tiết: Điểm điểm \(M\) thỏa mãn \(\overrightarrow {OM} = - 4\overrightarrow i + 5\overrightarrow k \) \( \Rightarrow M\left( { - 4;0;5} \right)\). Chọn A. Câu hỏi 26 : Trong không gian Oxyz, cho điểm \(M\left( {1; - 2;5} \right)\). Khoảng cách từ M đến trục Oz bằng
Đáp án: A Phương pháp giải: Khoảng cách từ điểm \(M\left( {a;b;c} \right)\) đến trục \(Oz\) là \(d\left( {M;Oz} \right) = \sqrt {{x^2} + {y^2}} \). Lời giải chi tiết: Khoảng cách từ điểm \(M\left( {1; - 2;5} \right)\) đến trục \(Oz\) là \(d\left( {M;Oz} \right) = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \). Chọn A. Câu hỏi 27 : Trong không gian Oxyz, cho điểm \(A\left( {2;3;5} \right)\). Tìm tọa độ điểm A’ là hình chiếu vuông góc của A lên trục Oy.
Đáp án: C Phương pháp giải: Trong không gian Oxyz, hình chiếu vuông góc của điểm \(A\left( {x;y;z} \right)\) lên trục \(Oy\) có tọa độ là \(\left( {0;y;0} \right)\). Lời giải chi tiết: Hình chiếu của điểm \(A\left( {2;3;5} \right)\) lên trục Oy là điểm \(A'\left( {0;3;0} \right).\) Chọn C. Câu hỏi 28 : Trong không gian Oxyz, các vecto đơn vị trên các trục Ox,Oy,Oz lần lượt là \(\overrightarrow i ,\,\,\overrightarrow j ,\,\,\overrightarrow k \) cho điểm \(M\left( {3; - 4;12} \right)\). Mệnh đề nào sau đây đúng?
Đáp án: D Phương pháp giải: Điểm \(M\left( {x;y;z} \right)\) thì \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \). Lời giải chi tiết: Ta có \(M\left( {3; - 4;12} \right)\)\( \Rightarrow \overrightarrow {OM} = 3\overrightarrow i - 4\overrightarrow j + 12\overrightarrow k \) Chọn D. Câu hỏi 29 : Trong không gian Oxyz, cho tam giác ABC có \(A\left( {1; - 2;1} \right),\) \(B\left( { - 1;3;4} \right),\) \(C\left( {0;2;1} \right)\). Trọng tâm của tam giác ABC có tọa độ là
Đáp án: D Phương pháp giải: Áp dụng công thức tính tọa độ trọng tâm của tam giác: \(\left\{ \begin{array}{l}x = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\y = \frac{{{y_A} + {y_B} + {y_C}}}{3}\\z = \frac{{{z_A} + {z_B} + {z_C}}}{3}\end{array} \right.\) Lời giải chi tiết: Gọi G là trọng tâm tam giác ABC thì tọa độ điểm G là \(\left\{ \begin{array}{l}x = \frac{{1 - 1 + 0}}{3} = 0\\y = \frac{{ - 2 + 3 + 2}}{3} = 1\\z = \frac{{1 + 4 + 1}}{3} = 2\end{array} \right.\)\( \Rightarrow G\left( {0;1;2} \right).\) Chọn D. Câu hỏi 30 : Trong không gian Oxyz, điểm đối xứng với \(A\left( {4;1; - 2} \right)\) qua mặt phẳng \(\left( {Oxz} \right)\) có tọa độ là
Đáp án: A Phương pháp giải: Trong không gian Oxyz, hình chiếu vuông góc của điểm \(A\left( {x;y;z} \right)\) lên mặt phẳng \(\left( {Oxz} \right)\) có tọa độ là \(\left( {x;0;z} \right)\). Lời giải chi tiết: Điểm đối xứng của \(A\left( {4;1; - 2} \right)\) qua mặt phẳng \(\left( {Oxz} \right)\) là điểm \(A'\left( {4; - 1; - 2} \right)\) Chọn A. Câu hỏi 31 : Trong không gian Oxyz, cho hai điểm\(A\left( {1;1; - 2} \right)\) và \(B\left( {3;0;1} \right)\). Vecto \(\overrightarrow {AB} \) có tọa độ là
Đáp án: C Phương pháp giải: Áp dụng công thức tính vecto khi biết hai điểm: \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right)\). Lời giải chi tiết: Ta có \(A\left( {1;1; - 2} \right),\,\,B\left( {3;0;1} \right)\)\( \Rightarrow \overrightarrow {AB} = \left( {2; - 1;3} \right).\) Chọn C. Câu hỏi 32 : Trong không gian Oxyz, vecto \(\overrightarrow x = \overrightarrow i - 3\overrightarrow j + 2\overrightarrow k \) có tọa độ là
Đáp án: B Phương pháp giải: Vecto \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j + c\overrightarrow k \Rightarrow \overrightarrow u = \left( {a;b;c} \right)\). Lời giải chi tiết: Ta có \(\overrightarrow x = \overrightarrow i - 3\overrightarrow j + 2\overrightarrow k \Rightarrow \overrightarrow x = \left( {1; - 3;2} \right)\) Chọn B. Câu hỏi 33 : Trong không gian Oxyz, cho \(\overrightarrow a = \left( { - 1;3;2} \right)\) và \(\overrightarrow b = \left( { - 3; - 1;2} \right)\). Tính \(\overrightarrow a .\overrightarrow b .\)
Đáp án: D Phương pháp giải: Sử dụng công thức tính tích vô hướng của 2 vectơ: \(\overrightarrow a = \left( {{x_1};{y_1};{z_1}} \right)\), \(\overrightarrow b \left( {{x_2};{y_2};{z_2}} \right)\)\( \Rightarrow \overrightarrow a .\overrightarrow b = {x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}\). Lời giải chi tiết: \(\overrightarrow a .\overrightarrow b = \left( { - 1} \right).\left( { - 3} \right) + 3.\left( { - 1} \right) + 2.2 = 3 - 3 + 4 = 4.\) Chọn D. Câu hỏi 34 : Trong không gian Oxyz, cho điểm \(A\left( { - 1;\,\,2;\,\,4} \right)\) và điểm \(B\left( {3;\,\,0; - 6} \right).\) Trung điểm của đoạn AB có tọa độ là:
Đáp án: A Phương pháp giải: Cho hai điểm \(A\left( {{x_1};\,{y_1};\,{z_1}} \right),\,\,B\left( {{x_2};\,{y_2};\,{z_2}} \right)\) thì tọa độ trung điểm của \(AB\) là: \(I\left( {\frac{{{x_1} + {x_2}}}{2};\,\,\frac{{{y_1} + {y_2}}}{2};\,\,\frac{{{z_1} + {z_2}}}{2}} \right).\) Lời giải chi tiết: Gọi \(I\left( {{x_I};\,\,{y_I};\,\,{z_I}} \right)\) là trung điểm của \(AB\) \( \Rightarrow I\left( {1;\,\,1;\, - 1} \right).\) Chọn A. Câu hỏi 35 : Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow a = - 2\overrightarrow i + 3\overrightarrow j + 5\overrightarrow k \). Tọa độ của vectơ \(\overrightarrow a \) là:
Đáp án: B Phương pháp giải: Cho vecto \(\overrightarrow a = {a_1}\overrightarrow i + {a_2}\overrightarrow j + {a_3}\overrightarrow k \Rightarrow \overrightarrow a = \left( {{a_1};\;{a_2};\;{a_3}} \right).\) Lời giải chi tiết: Ta có: \(\overrightarrow a = - 2\overrightarrow i + 3\overrightarrow j + 5\overrightarrow k = \left( { - 2;\,\,3;\,\,5} \right).\) Chọn B. Câu hỏi 36 : Trong không gian \(Oxyz,\) vecto đơn vị trên trục \(Oy\) là:
Đáp án: A Phương pháp giải: Trong không gian \(Oxyz,\) vecto đơn vị trên trục \(Oy\) là: \(\overrightarrow j \left( {0;\,\,1;\,\,0} \right).\) Lời giải chi tiết: Trong không gian \(Oxyz,\) vecto đơn vị trên trục \(Oy\) là: \(\overrightarrow j \left( {0;\,\,1;\,\,0} \right).\) Chọn A. Câu hỏi 37 : Trong không gian Oxyz , cho \(\overrightarrow a = \left( { - 2; - 3;3} \right),\) \(\overrightarrow b = \left( {0;2; - 1} \right),\) \(\overrightarrow c = \left( { - 3;2;5} \right)\). Tìm tọa độ của vectơ \(\overrightarrow u = 2\overrightarrow a - 3\overrightarrow b + 4\overrightarrow c \).
Đáp án: C Phương pháp giải: - Sử dụng công thức \(\overrightarrow u = \left( {a;b;c} \right) \Rightarrow k\overrightarrow u = \left( {ka;kb;kc} \right)\)\(\left( {k \ne 0} \right)\). - Cộng hai vectơ: \(\overrightarrow u \left( {{x_1};{y_1};{z_2}} \right);\,\,\overrightarrow v \left( {{x_2};{y_2};{z_2}} \right)\)\( \Rightarrow \overrightarrow u + \overrightarrow v = \left( {{x_1} + {x_2};{y_1} + {y_2};{z_1} + {z_2}} \right)\). Lời giải chi tiết: \(\begin{array}{l}\overrightarrow u = 2\overrightarrow a - 3\overrightarrow b + 4\overrightarrow c \\\,\,\,\, = 2\left( { - 2; - 3;3} \right) - 3\left( {0;2; - 1} \right) + 4\left( { - 3;2;5} \right)\\\,\,\,\, = \left( { - 4; - 6;6} \right) - \left( {0;6; - 3} \right) + \left( { - 12;8;20} \right)\\\,\,\,\, = \left( { - 16; - 4;29} \right)\end{array}\) Chọn C. Câu hỏi 38 : Trong không gian Oxzy, cho hai điểm A(1;1;-1) và B(1;2;2). Độ dài đoạn thẳng AB là:
Đáp án: C Phương pháp giải: Áp dụng công thức tính độ dài đoạn thẳng \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \). Lời giải chi tiết: \(AB = \sqrt {{{\left( {1 - 1} \right)}^2} + {{\left( {2 - 1} \right)}^2} + {{\left( {2 + 1} \right)}^2}} = \sqrt {10} \). Chọn C. Câu hỏi 39 : Trong không gian cho ba điểm \(A\left( {5; - 2;0} \right)\), \(B\left( { - 2;3;0} \right)\), \(C\left( {0;2;3} \right)\). Trọng tâm \(G\) của tam giác \(ABC\) có tọa độ là
Đáp án: B Phương pháp giải: Cho \(\Delta ABC\) có \(A\left( {{x_1};{y_1};{z_1}} \right),\)\(B\left( {{x_2};{y_2};{z_2}} \right),\)\(C\left( {{x_3};{y_3};{z_3}} \right).\) Trọng tâm \(G\) của tam giác \(ABC\) có tọa độ: \(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_1} + {x_2} + {x_3}}}{3}\\{y_G} = \dfrac{{{y_1} + {y_2} + {y_3}}}{3}\\{z_G} = \dfrac{{{z_1} + {z_2} + {z_3}}}{3}\end{array} \right.\) Lời giải chi tiết: Trọng tâm \(G\) có tọa độ \(\left\{ \begin{array}{l}{x_G} = \dfrac{{5 + \left( { - 2} \right) + 0}}{3} = 1\\{y_G} = \dfrac{{ - 2 + 3 + 2}}{3} = 1\\{z_G} = \dfrac{{0 + 0 + 3}}{3} = 1\end{array} \right.\) . Hay \(G\left( {1;1;1} \right)\) Chọn B. Câu hỏi 40 : Trong không gian với hệ tọa độ Oxyz , hình chiếu của điểm \(M\left( {1; - 3; - 5} \right)\) trên trục Ox có tọa độ là:
Đáp án: B Phương pháp giải: Hình chiếu của điểm \(A\left( {a;b;c} \right)\) lên trục Ox là \(A'\left( {a;0;0} \right)\). Lời giải chi tiết: Hình chiếu của điểm \(M\left( {1; - 3; - 5} \right)\) trên trục Ox là \(M'\left( {1;0;0} \right)\). Chọn B. Câu hỏi 41 : Trong không gian Oxyz, hình chiếu vuông góc của điểm \(M\left( {1;\,\,6;\,\,2020} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) có tọa độ là:
Đáp án: B Phương pháp giải: Điểm \(M'\) là hình chiếu của điểm \(M\left( {a;\,\,b;\,\,c} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) có tọa độ là: \(M'\left( {0;\,\,b;\,\,c} \right).\) Lời giải chi tiết: Tọa độ hình chiếu vuông góc của điểm \(M\left( {1;\,\,6;\,\,2020} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) có tọa độ là: \(\left( {0;\,\,6;\,\,2020} \right).\) Chọn B. Câu hỏi 42 : Trong không gian \(Oxyz,\) cho hai vecto \(\overrightarrow u = \left( {1;\,\,4;\,\,1} \right)\) và \(\overrightarrow v = \left( { - 1;\,\,1; - 3} \right).\) Góc tạo bởi hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) là:
Đáp án: B Phương pháp giải: Cho hai vecto \(\overrightarrow a \left( {{x_1};\,\,{y_1};\,\,{z_1}} \right),\,\,\,\overrightarrow b = \left( {{x_2};\,\,{y_2};\,\,{z_2}} \right).\) Khi đó \(\alpha = \angle \left( {\overrightarrow a ;\,\,\overrightarrow b } \right)\) có: \(\cos \alpha = \dfrac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \dfrac{{{x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}}}{{\sqrt {x_1^2 + y_1^2 + z_1^2} .\sqrt {x_2^2 + y_2^2 + z_2^2} }}.\) Lời giải chi tiết: Cho hai vecto \(\overrightarrow u = \left( {1;\,\,4;\,\,1} \right)\) và \(\overrightarrow v = \left( { - 1;\,\,1; - 3} \right)\) \(\begin{array}{l} \Rightarrow \cos \left( {\overrightarrow u ,\,\,\overrightarrow v } \right) = \dfrac{{1.\left( { - 1} \right) + 4.1 + 1.\left( { - 3} \right)}}{{\sqrt {{1^2} + {4^2} + {1^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {1^2} + {{\left( { - 3} \right)}^2}} }} = 0\\ \Rightarrow \angle \left( {\overrightarrow u ,\,\,\overrightarrow v } \right) = {90^0}.\end{array}\) Chọn B. Câu hỏi 43 : Trong không gian \(Oxyz,\) cho điểm \(A\left( { - 4;\,\,3;\,\,12} \right).\) Độ dài đoạn thẳng \(OA\) bằng:
Đáp án: A Phương pháp giải: Cho hai điểm \(A\left( {{x_1};\,\,{y_1};\,\,{z_1}} \right)\) và \(B\left( {{x_2};\,\,{y_2};\,\,{z_2}} \right) \Rightarrow \overrightarrow {AB} = \left( {{x_2} - {x_1};\,\,{y_2} - {y_1};\,\,{z_2} - {z_1}} \right).\) \( \Rightarrow \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} .\) Lời giải chi tiết: Ta có: \(\overrightarrow {OA} = \left( { - 4;\,\,3;\,\,12} \right)\) \( \Rightarrow OA = \sqrt {{{\left( { - 4} \right)}^2} + {3^2} + {{12}^2}} = \sqrt {169} = 13.\) Chọn A. Câu hỏi 44 : Trong không gian \(Oxyz,\) cho tam giác \(ABC\) có \(A\left( {1;\,\,2;\,\,1} \right),\,\,\,B\left( {1;\,\,0;\,\,1} \right)\) và \(C\left( {1;\,\,1;\,\,2} \right).\) Diện tích tam giác \(ABC\) bằng:
Đáp án: A Phương pháp giải: Sử dụng công thức \({S_{\Delta ABC}} = \dfrac{1}{2}\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right]\). Lời giải chi tiết: Ta có: \(\overrightarrow {AB} = \left( {0; - 2;0} \right),\,\,\overrightarrow {AC} = \left( {0; - 1;1} \right)\) \( \Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( { - 2;0;0} \right)\). Vậy \({S_{\Delta ABC}} = \dfrac{1}{2}\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \dfrac{1}{2}\sqrt {{{\left( { - 2} \right)}^2} + {0^2} + {0^2}} = 1.\) Chọn A. Câu hỏi 45 : Trong không gian với hệ tọa độ \(Oxyz\), cho hai điểm \(A\left( {1;0;1} \right)\) và \(B\left( {4;2; - 2} \right)\). Độ dài đoạn thẳng \(AB\) bằng:
Đáp án: C Phương pháp giải: Sử dụng công thức tính độ dài đoạn thẳng \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \). Lời giải chi tiết: \(AB = \sqrt {{3^2} + {2^2} + {{\left( { - 3} \right)}^2}} = \sqrt {22} \). Chọn C. Câu hỏi 46 : Trong không gian \(Oxyz,\) hình chiếu vuông góc của điểm \(M\left( {1; - 2;\,\,3} \right)\) lên mặt phẳng \(\left( {Oyz} \right)\) là:
Đáp án: B Phương pháp giải: Hình chiếu vuông góc của điểm \(M\left( {{x_0};\,\,{y_0};\,\,{z_0}} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) là \(M'\left( {0;\,\,{y_0};\,\,{z_0}} \right).\) Lời giải chi tiết: Hình chiếu vuông góc của điểm \(M\left( {1; - 2;\,\,3} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) là \(A\left( {0;\, - 2;\,\,3} \right).\) Chọn B. Câu hỏi 47 : Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow u = 2\overrightarrow i - 3\overrightarrow k \), khi đó:
Đáp án: C Phương pháp giải: Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j + c\overrightarrow k \), khi đó: \(\overrightarrow u = \left( {a;b;c} \right)\). Lời giải chi tiết: Trong không gian \(Oxyz\), cho vectơ \(\overrightarrow u = 2\overrightarrow i - 3\overrightarrow k \), khi đó: \(\overrightarrow u = \left( {2;0; - 3} \right)\). Chọn C. Câu hỏi 48 : Trong không gian \(Oxyz\), cho \(\overrightarrow {OA} = 3\overrightarrow i - 2\overrightarrow j - \overrightarrow k \). Tọa độ của điểm \(A\) là:
Đáp án: B Phương pháp giải: \(\overrightarrow {OA} = a\overrightarrow i + b\overrightarrow j + c\overrightarrow k \Rightarrow A\left( {a;b;c} \right)\). Lời giải chi tiết: Ta có \(\overrightarrow {OA} = 3\overrightarrow i - 2\overrightarrow j - 1\overrightarrow k \Rightarrow A\left( {3; - 2; - 1} \right)\). Chọn B. Câu hỏi 49 : Trong không gian \(Oxyz\), hình chiếu vuông góc của điểm trên trục \(Oy\) là điểm
Đáp án: B Phương pháp giải: Hình chiếu vuông góc của điểm \(M\left( {x;y;z} \right)\) trên trục \(Oy\) là \(M'\left( {0;y;0} \right)\). Lời giải chi tiết: Hình chiếu vuông góc của điểm \(M\left( {3;1;2} \right)\) trên trục \(Oy\) là điểm \(F\left( {0;1;0} \right)\). Chọn B. Câu hỏi 50 : Trong không gian \(Oxyz\) cho ba vecto \(\overrightarrow a = \left( { - 1;1;0} \right),\)\(\overrightarrow b = \left( {2;2;0} \right),\)\(\overrightarrow c = \left( {1;1;1} \right)\). Trong các khẳng định sau khẳng định nào sai ?
Đáp án: D Phương pháp giải: Kiểm tra tính đúng sai của từng đáp án, sử dụng các công thức nhân vô hướng hai véc tơ, độ dài véc tơ và chú ý: \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = 0\). Lời giải chi tiết: Đáp án A: \(\overrightarrow a .\overrightarrow b = - 1.2 + 1.2 + 0.0 = 0\) nên \(\overrightarrow a \bot \overrightarrow b \) hay A đúng. Đáp án B: \(\left| {\overrightarrow a } \right| = \sqrt {{{\left( { - 1} \right)}^2} + {1^2} + {0^2}} = \sqrt 2 \) nên B đúng. Đáp án C: \(\left| {\overrightarrow c } \right| = \sqrt {{1^2} + {1^2} + {1^2}} = \sqrt 3 \) nên C đúng. Đáp án D: \(\overrightarrow c .\overrightarrow b = 1.2 + 1.2 + 1.0 = 4 \ne 0\) nên \(\overrightarrow c \) và \(\overrightarrow b \) không vuông góc hay D sai. Chọn D.
|