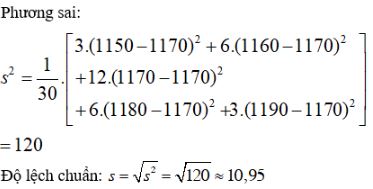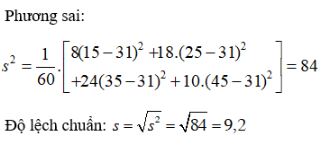Bài 1 trang 128 SGK Đại số 10Tính phương sai và độ lệch chuẩn của bảng ... Đề bài Tính phương sai và độ lệch chuẩn của bảng phân bố tần số đã được lập ở bài tập 1 và của bảng phân bố tần số ghép lớp cho ở bài tập 2 của \(\S 1.\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Công thức tính phương sai: +) Trong bảng phân bố tần số: \({s^2} = \dfrac{{{n_1}{{\left( {{n_1} - \overline x } \right)}^2} + {n_2}{{\left( {{n_2} - \overline x } \right)}^2} + ........ + {n_k}{{\left( {{n_k} - \overline x } \right)}^2}}}{n}.\) +) Trong bảng phân bố tần số ghép lớp: \({s^2} = \dfrac{{{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ........ + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}}}{n}.\) Công thức tính độ lệch chuẩn: \(s = \sqrt{s^2}.\) Lời giải chi tiết a) Phương sai và độ lệch chuẩn trong bài tập 1. Bảng phân bố tần số viết lại là Số trung bình: \(\overline{x}=\dfrac{1}{30}.(3\times1150 + 6\times1160 \)\(+ 12\times1170 + 6\times 1180 + 3\times 1190) \)\( = 1170\). Cách khác: Phương sai: \(S_{x}^{2}=\dfrac{1}{30}(3\times1150^{2}+6\times1160^{2}\)\(+12\times1170^{2}+6\times1180^{2}+3\times1190^{2})\)\(-1170^{2}= 120\) Độ lệch chuẩn: \(S_x= \sqrt{S_{x}^{2}}=\sqrt{120} ≈ 10,95\). b) Phương sai và độ lệch chuẩn, bảng thống kê trong bài tập 2 \(\S 1.\) Số trung bình cộng: \(\overline x = \dfrac{{13,3}}{{100}}.15 + \dfrac{{30}}{{100}}.25\) \( + \dfrac{{40}}{{100}}.35 + \dfrac{{16,7}}{{100}}.45 \approx 31\) Cách khác: Phương sai: \(S_{x}^{2}=\dfrac{1}{60}(8\times15^{2}+18\times25^{2}\)\(+24\times35^{2}+10\times45^{2})- 31^2= 84 \) Độ lệch chuẩn: \( S_x≈ 9,2\). HocTot.XYZ
|