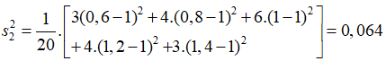Bài 3 trang 128 SGK Đại số 10Cho hai bảng phân bố tần số ghép lớp... Video hướng dẫn giải Cho hai bảng phân bố tần số ghép lớp Khối lượng của nhóm cá mè thứ 1 Khối lượng của nhóm cá mè thứ 2 LG a Tính các số trung bình cộng của các bảng phân bố tần số ghép lớp đã cho. Phương pháp giải: Công thức tính trung bình cộng: +) Trong bảng phân bố tần số: \(\overline x = \frac{{{x_1}{n_1} + {x_2}{n_2} + ....... + {x_k}{n_k}}}{n}.\) +) Trong bảng phân bố tần số ghép lớp: \(\overline x = \frac{{{c_1}{n_1} + {c_2}{n_2} + ....... + {c_k}{n_k}}}{n}.\) Lời giải chi tiết: - Số trung bình cộng của nhóm cá thứ nhất: \(\overline{x}=\frac{1}{20}.(4\times0,7 + 6\times0,9 \)\(+ 6\times 1,1 + 4\times 1,3) = 1\) - Số trung bình cộng của nhóm cá thứ hai: \(\overline{y}=\frac{1}{20}.(3\times0,6 + 4\times0,8 + 6\times1 \)\(+ 4\times1,2 + 3\times1,4) = 1\) LG b Tính phương sai của các bảng phân bố tần số ghép lớp đã cho. Phương pháp giải: Công thức tính phương sai: +) Trong bảng phân bố tần số: \({s^2} = \frac{{{n_1}{{\left( {{n_1} - \overline x } \right)}^2} + {n_2}{{\left( {{n_2} - \overline x } \right)}^2} + ........ + {n_k}{{\left( {{n_k} - \overline x } \right)}^2}}}{n}.\) +) Trong bảng phân bố tần số ghép lớp: \({s^2} = \frac{{{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ........ + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}}}{n}.\) Cách 2: \({s^2} = \overline {{x^2}} - {\left( {\overline x } \right)^2}.\) với \(\overline {{x^2}} = \frac{{x_1^2{n_1} + x_2^2{n_2} + ....... + x_k^2{n_k}}}{n}.\) Lời giải chi tiết: - Đối với nhóm cá thứ nhất: + Phương sai: \(S_{x}^{2}=\dfrac{1}{20}.(4\times0,7^2 + 6\times0,9^2 \)\(+ 6\times1,1^2 + 4\times1,3^2) – 1 = 0,042\) + Độ lệch chuẩn: \(S_x≈ 0,2\) - Đối với nhóm cá thứ hai: + Phương sai: \(S_{y}^{2}=\dfrac{1}{20}.(3\times0,6^2 + 4\times0,8^2 + 6\times1^2 \)\(+ 4\times1,2^2 + 3\times 1,4^2) – 1 = 0,064\) + Độ lệch chuẩn: \(S_x= \sqrt{0,064} ≈ 0,25\). Cách khác: Phương sai nhóm cá thứ nhất: Phương sai nhóm cá thứ hai LG c Xét xem nhóm cá nào có khối lượng đồng đều hơn? Lời giải chi tiết: Ta thấy \(\overline{x}=\overline{y}= 1\), trọng lượng trung bình hai nhóm cá bằng nhau nhưng \(S_{x}^{2} < S_{y}^{2}\) chứng tỏ mức độ phân tán các giá trị so với giá trị trung bình của nhóm cá thứ hai lớn hơn. Nghĩa là khối lượng nhóm cá thứ nhất đồng đều hơn nhóm cá thứ hai. HocTot.XYZ
|