Bài 1 trang 7 SGK Đại số và Giải tích 12 Nâng caoXét chiều biến thiên của các hàm số sau:
Lựa chọn câu để xem lời giải nhanh hơn
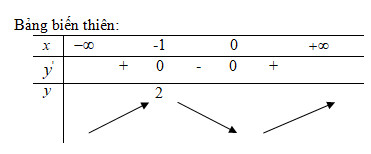
Xét chiều biến thiên của các hàm số sau: LG a \(y = 2{x^3} + 3{x^2} + 1\) Lời giải chi tiết: Tập xác định: \(D =\mathbb R\) \(\eqalign{
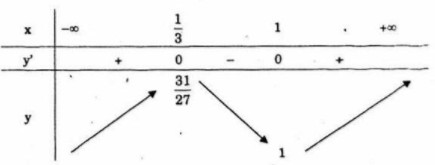
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0; + \infty } \right)\) nghịch biến trên khoảng \(\left( { - 1;0} \right)\). LG b \(y = {x^3} - 2{x^2} + x + 1\) Lời giải chi tiết: Tập xác định: \(D =\mathbb R\) \(\eqalign{ Bảng biến thiên
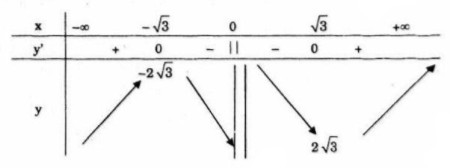
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ;{1 \over 3}} \right)\) và \(\,\left( {1; + \infty } \right)\) , nghịch biến trên khoảng \(\,\left( {{1 \over 3};1} \right)\). LG c \(y = x + {3 \over x}\) Lời giải chi tiết: Tập xác định: \(D =\mathbb R\backslash \left\{ 0 \right\}\) \(\eqalign{ Bảng biến thiên
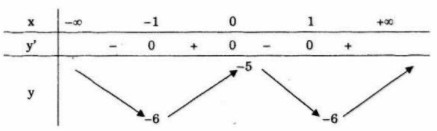
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - \sqrt 3 } \right)\) và \(\,\left( {\sqrt 3 ; + \infty } \right)\) , nghịch biến trên khoảng \(\left( { - \sqrt 3 ;0} \right)\) và \(\,\left( {0;\sqrt 3 } \right)\). LG d \(y = x - {2 \over x}\) Lời giải chi tiết: Tập xác định: \(D = \mathbb R\backslash \left\{ 0 \right\}\) \(y' = 1 + {2 \over {{x^2}}} > 0\) với mọi \(x \ne 0\) Hàm số đồng biến trên mỗi khoảng \(\,\,\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\). LG e \(y = {x^4} - 2{x^2} - 5\) Lời giải chi tiết: Tập xác định: \(D= \mathbb R\) \(y' = 4{x^3} - 4x = 4x\left( {{x^2} - 1} \right);y' = 0 \) \( \Leftrightarrow \,\left[ \matrix{ Bảng biến thiên
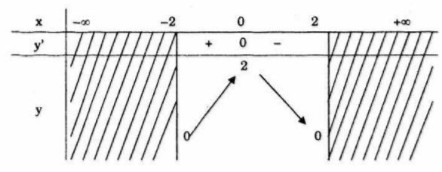
Hàm số nghịch biến trên mỗi khoảng \(\,\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\), đồng biến trên mỗi khoảng \(\left( { - 1;0} \right)\) và \(\left( {1; + \infty } \right)\). LG f \(y = \sqrt {4 - {x^2}} \) Lời giải chi tiết: Hàm số xác định khi và chỉ khi \(4 - {x^2} \ge 0 \Leftrightarrow - 2 \le x \le 2\) Tập xác định: \(D = \left[ { - 2;2} \right]\) \(y' = {{ - 2x} \over {2\sqrt {4 - {x^2}} }} = {{ - x} \over {\sqrt {4 - {x^2}} }};\) \(y' = 0 \Leftrightarrow \)\(x = 0\) Bảng biến thiên
Hàm số đồng biến trên khoảng \(\left( { - 2;0} \right)\) và nghịch biến trên khoảng \(\left( {0;2} \right)\) . HocTot.XYZ
|