Bài 14 trang 53 SGK Hình học 12Một hình tứ diện đều cạnh a có một đỉnh trùng với đỉnh của hình nón. Đề bài Một hình tứ diện đều cạnh \(a\) có một đỉnh trùng với đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón. Khi đó diện tích xung quanh của hình nón là: (A) \({1 \over 2}\pi {a^2}\sqrt 3 \) ; (B) \({1 \over 3}\pi {a^2}\sqrt 2 \) ; (C) \({1 \over 3}\pi {a^2}\sqrt 3 \) ; (D) \(\pi {a^2}\sqrt 3 \) . Video hướng dẫn giải Phương pháp giải - Xem chi tiết Diện tích xung quanh của hình nón \({S_{xq}} = \pi rl\), trong đó \(r;l\) lần lượt là bán kính đáy và độ dài đường sinh của hình nón. +) Bán kính đáy của hình nón chính là bán kính đường tròn ngoại tiếp tam giác đều cạnh \(a\). +) Độ dài đường sinh của hình nón chính là độ dài cạnh bên của tứ diện. Lời giải chi tiết
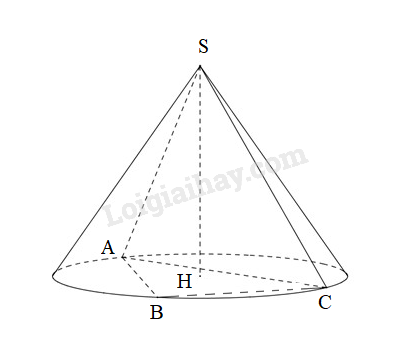
Giả sử có tứ diện đều \(SABC\) , hình nón có đỉnh trùng với \(S\) và đáy là đường tròn ngoại tiếp tam giác \(ABC\) bán kính đường tròn đáy bằng \({2\over3}\) độ dài trung tuyến \(ABC\) \(r = {2 \over 3}.{{a\sqrt 3 } \over 2} = {{a\sqrt 3 } \over 3}\) Đường sinh hình nón bằng cạnh \(SA=a\). Diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = {1 \over 3}\pi {a^2}\sqrt 3 \) Chọn (C). HocTot.XYZ
|