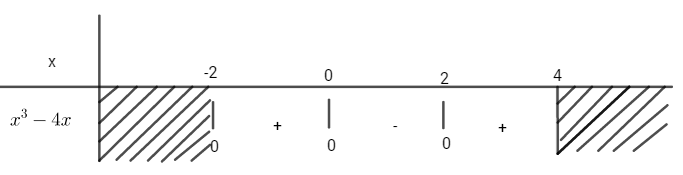Bài 28 Trang 167 SGK Đại số và Giải tích 12 Nâng caoTính diện tích hình phẳng giới hạn bởi:
Lựa chọn câu để xem lời giải nhanh hơn
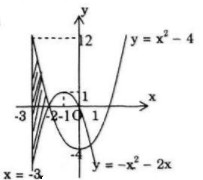
Tính diện tích hình phẳng giới hạn bởi: LG a Đồ thị các hàm số \(y = {x^2} - 4\), \(y = - {x^2} - 2x\) và đường thẳng \(x = - 3,x = - 2;\) Phương pháp giải: Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right),\) \(x = a,x = b\). +) B1: Tìm nghiệm \(a \le {x_1} < {x_2} < ... < {x_n} \le b\) của phương trình hoành độ giao điểm \(f\left( x \right) = g\left( x \right)\). +) B2: Tính diện tích theo công thức: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( = \int\limits_a^{{x_1}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( + \int\limits_{{x_1}}^{{x_2}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( + ... + \int\limits_{{x_{n - 1}}}^{{x_n}} {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( + \int\limits_{{x_n}}^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \) \( = \left| {\int\limits_a^{{x_1}} {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\)\( + \left| {\int\limits_{{x_1}}^{{x_2}} {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\) \( + ... + \left| {\int\limits_{{x_{n - 1}}}^{{x_n}} {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\) \( + \left| {\int\limits_{{x_n}}^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } \right|\) Lời giải chi tiết: Cách 1: Tính diện tích theo công thức Ta có: \({x^2} - 4 = - {x^2} - 2x\) \( \Leftrightarrow 2{x^2} + 2x - 4 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\) Có \( - 3 < - 2 < 1\) nên \(S = \int\limits_{ - 3}^{ - 2} {\left| {{x^2} - 4 - \left( { - {x^2} - 2x} \right)} \right|dx} \) \( = \int\limits_{ - 3}^{ - 2} {\left| {2{x^2} + 2x - 4} \right|dx} \) \( = \left| {\int\limits_{ - 3}^{ - 2} {\left( {2{x^2} + 2x - 4} \right)dx} } \right|\) \( = \left| {\left( {2.\frac{{{x^3}}}{3} + 2.\frac{{{x^2}}}{2} - 4x} \right)_{ - 3}^{ - 2}} \right|\) \( = \left| {\frac{{20}}{3} - 3} \right| = \frac{{11}}{3}\) Cách 2: Xét dấu Ta có
Ta thấy, khi \( - 3 \le x \le - 2\) thì \(2{x^2} + 2x - 4 \ge 0\) \( \Rightarrow \left| {2{x^2} + 2x - 4} \right| = 2{x^2} + 2x - 4\). Do đó, \(S = \int\limits_{ - 3}^{ - 2} {\left| {{x^2} - 4 - \left( { - {x^2} - 2x} \right)} \right|} dx \) \(= \int\limits_{ - 3}^{ - 2} {\left( {2{x^2} + 2x - 4} \right)} dx\) \( = 2\int\limits_{ - 3}^{ - 2} {\left( {{x^2} + x - 2} \right)} dx\) \( = 2\left. {\left( {{{{x^3}} \over 3} + {{{x^2}} \over 2} - 2x} \right)} \right|_{ - 3}^{ - 2} = {{11} \over 3}\) Chú ý: Khi việc xét dấu phức tạp ta nên làm theo cách 1 sẽ tránh được việc lập bảng xét dấu. LG b Đồ thị hai hàm số \(y = {x^2}\) và \(y = - {x^2} - 2x\) Lời giải chi tiết: Cách 1: Phương trình hoành độ giao điểm của hai đồ thị là: \({x^2} - 4 = - {x^2} - 2x \Leftrightarrow {x^2} + x - 2 = 0 \) \(\Leftrightarrow \left[ \matrix{ \(S = \int\limits_{ - 2}^1 {\left| {{x^2} - 4 - \left( { - {x^2} - 2x} \right)} \right|dx} \) \( = \int\limits_{ - 2}^1 {\left| {2{x^2} + 2x - 4} \right|dx} \) \( = \left| {\int\limits_{ - 2}^1 {\left( {2{x^2} + 2x - 4} \right)dx} } \right|\) \( = \left| {\left( {\dfrac{{2{x^3}}}{3} + \dfrac{{2{x^2}}}{2} - 4x} \right)_{ - 2}^1} \right|\) \( = \left| { - \dfrac{7}{3} - \dfrac{{20}}{3}} \right| = \left| { - 9} \right| = 9\) Cách 2: Phương trình hoành độ giao điểm của hai đồ thị là: \({x^2} - 4 = - {x^2} - 2x \Leftrightarrow {x^2} + x - 2 = 0 \) \(\Leftrightarrow \left[ \matrix{ Ta thấy, khi \( - 2 \le x \le 1\) thì \(2{x^2} + 2x - 4 \le 0\) \( \Rightarrow \left| {2{x^2} + 2x - 4} \right| = -2{x^2} - 2x + 4\). Do đó, \(S = \int\limits_{ - 2}^1 {\left| {{x^2} - 4 - \left( { - {x^2} - 2x} \right)} \right|} dx \) \(= \int\limits_{ - 2}^1 {\left| {2{x^2} + 2x - 4} \right|} dx\) \( = \int\limits_{ - 2}^1 {\left( { - 2{x^2} - 2x + 4} \right)} dx \) \(= \left. {\left( { - {{2{x^3}} \over 3} - {x^2} + 4x} \right)} \right|_{ - 2}^1 = 9\) LG c Đồ thị hàm số \(y = {x^3} - 4x\), trục hoành, đường thẳng x=-2 và đường thẳng x=4 Lời giải chi tiết: Cách 1: Ta có: \({x^3} - 4x = 0 \Leftrightarrow x\left( {{x^2} - 4} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x = - 2\end{array} \right.\) Ta thấy, \( - 2 < 0 < 2 < 4\) \( \Rightarrow S = \int\limits_{ - 2}^4 {\left| {{x^3} - 4x} \right|dx} \) \( = \int\limits_{ - 2}^0 {\left| {{x^3} - 4x} \right|dx} + \int\limits_0^2 {\left| {{x^3} - 4x} \right|dx} \) \(+ \int\limits_2^4 {\left| {{x^3} - 4x} \right|dx}\) \( = \left| {\int\limits_{ - 2}^0 {\left( {{x^3} - 4x} \right)dx} } \right| + \left| {\int\limits_0^2 {\left( {{x^3} - 4x} \right)dx} } \right|\) \(+ \left| {\int\limits_2^4 {\left( {{x^3} - 4x} \right)dx} } \right|\) \( = \left| {\left( {\dfrac{{{x^4}}}{4} - \dfrac{{4{x^2}}}{2}} \right)_{ - 2}^0} \right| + \left| {\left( {\dfrac{{{x^4}}}{4} - \dfrac{{4{x^2}}}{2}} \right)_0^2} \right|\) \(+ \left| {\left( {\dfrac{{{x^4}}}{4} - \dfrac{{4{x^2}}}{2}} \right)_2^4} \right|\) \( = \left| {0 - \left( { - 4} \right)} \right| + \left| { - 4 - 0} \right|+ \left| { 32 - (-4)} \right|\) \( = 44\) Cách 2:
\(S = \int\limits_{ - 2}^4 {\left| {{x^3} - 4x} \right|} dx \) \(= \int\limits_{ - 2}^0 {\left( {{x^3} - 4x} \right)} dx - \int\limits_0^2 {\left( {{x^3} - 4x} \right)} dx \) \(+ \int\limits_2^4 {\left( {{x^3} - 4x} \right)} dx \) \( = \left( {\dfrac{{{x^4}}}{4} - \dfrac{{4{x^2}}}{2}} \right)_{ - 2}^0 - \left( {\dfrac{{{x^4}}}{4} - \dfrac{{4{x^2}}}{2}} \right)_0^2\) \( + \left( {\dfrac{{{x^4}}}{4} - \dfrac{{4{x^2}}}{2}} \right)_2^4\) \( = 4 - \left( { - 4} \right) + 36\) \(= 44\) HocTot.XYZ
|