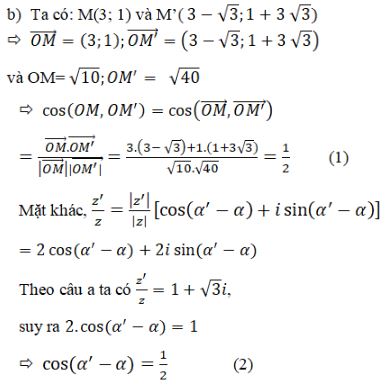Bài 30 trang 206 SGK giải tích 12 nâng caoChứng minh rằng hiệu số acgumen của z’ với acgumen của z là một số đo của góc lượng giác
Lựa chọn câu để xem lời giải nhanh hơn
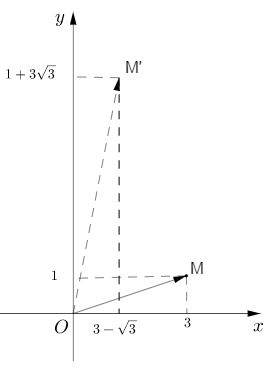
Gọi M, M’ là các điểm trong mặt phẳng phức theo thứ tự biểu diễn các số \(z = 3 + i;\) \(z' = \left( {3 - \sqrt 3 } \right) + \left( {1 + 3\sqrt 3 } \right)i.\) LG a Tính \({{z'} \over z};\) Phương pháp giải: Sử dụng công thức chia hai số phức: \(\dfrac{{a + bi}}{{c + di}} = \dfrac{{\left( {a + bi} \right)\left( {c - di} \right)}}{{{c^2} + {d^2}}}\) Lời giải chi tiết: \(\frac{{z'}}{z} = \frac{{3 - \sqrt 3 + \left( {1 + 3\sqrt 3 } \right)i}}{{3 + i}}\) \(= {{\left[ {3 - \sqrt 3 + \left( {1 + 3\sqrt 3 } \right)i} \right]\left( {3 - i} \right)} \over {3^2+1^2}}\) \( = \frac{{9 - 3\sqrt 3 + 1 + 3\sqrt 3 + \left( {3 + 9\sqrt 3 - 3 + \sqrt 3 } \right)i}}{{10}} \) \(= \frac{{10 + 10\sqrt 3 i}}{{10}}\) \( = 1 + \sqrt 3 i\) LG b Chứng minh rằng hiệu số acgumen của z’ với acgumen của z là một số đo của góc lượng giác \(\left( {OM,OM'} \right)\). Tính số đo đó. Phương pháp giải: Dựng hình, suy ra kết luận từ hình vẽ. Lời giải chi tiết:
Xét tia Ox thì ta có: \(sđ\left( {OM,OM'} \right) \) \(= sđ\left( {Ox,OM'} \right) - sđ\left( {Ox,OM} \right)\) \( = \varphi ' - \varphi = acgumen{{z'} \over z}\) (sai khác \(k2\pi \)) (trong đó \(\varphi \) và \(\varphi '\) theo thứ tự là acgumen của z và z’). Từ đó do \({{z'} \over z} = 1 + \sqrt 3 i\) có acgumen là \({\pi \over 3} + k2\pi \,\,\left( {k \in Z} \right)\), nên góc lượng giác \(\left( {OM,OM'} \right)\) có số đo \({\pi \over 3} + k2\pi \,\,\left( {k \in\mathbb Z} \right)\) Cách khác: Từ (1) và (2) ta có: cos(α'-α)=cos(OM,OM') nên kí hiệu α'-α là một số đo của góc lượng giác (OM, OM’) và số đo là \(\alpha ' - \alpha = \frac{\pi }{3} + k2\pi \). HocTot.XYZ
|