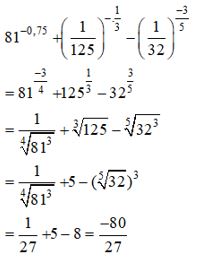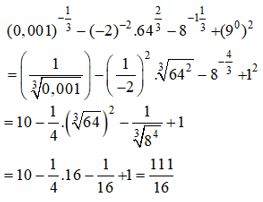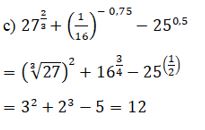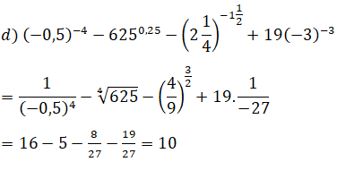Bài 4 trang 76 SGK Đại số và Giải tích 12 Nâng caoThực hiện phép tính:
Lựa chọn câu để xem lời giải nhanh hơn
Thực hiện phép tính: a) \({81^{ - 0,75}} + {\left( {{1 \over {125}}} \right)^{{{ - 1} \over 3}}} - {\left( {{1 \over {32}}} \right)^{{{ - 3} \over 5}}};\) b) \(0,{001^{{{ - 1} \over 3}}} - {\left( { - 2} \right)^{ - 2}}{.64^{{2 \over 3}}} - {8^{ - 1{1 \over 3}}}\) \( + {\left( {{9^0}} \right)^2};\) c) \({27^{{2 \over 3}}} + {\left( {{1 \over {16}}} \right)^{ - 0,75}} - {25^{0,5}}\) d) \({\left( { - 0,5} \right)^{ - 4}} - {625^{0,25}} - {\left( {2{1 \over 4}} \right)^{ - 1{1 \over 2}}} \) \(+ 19{\left( { - 3} \right)^{ - 3}}\) LG a \({81^{ - 0,75}} + {\left( {{1 \over {125}}} \right)^{{{ - 1} \over 3}}} - {\left( {{1 \over {32}}} \right)^{{{ - 3} \over 5}}};\) Lời giải chi tiết: \({81^{ - 0,75}} + {\left( {{1 \over {125}}} \right)^{{{ - 1} \over 3}}} - {\left( {{1 \over {32}}} \right)^{{{ - 3} \over 5}}} \) \(= {\left( {{3^4}} \right)^{ {{ - 3} \over 4}}} + {\left( {{{\left( {{1 \over 5}} \right)}^3}} \right)^{{{ - 1} \over 3}}} - {\left( {{{\left( {{1 \over 2}} \right)}^5}} \right)^{{{ - 3} \over 5}}}\) \(\, = {\left( 3 \right)^{ - 3}} + {\left( {{1 \over 5}} \right)^{ - 1}} - {\left( {{1 \over 2}} \right)^{ - 3}}\) \(= {1 \over {27}} + 5 - 8 = {1 \over {27}} - 3 = - {{80} \over {27}}\) Cách khác: LG b \(0,{001^{{{ - 1} \over 3}}} - {\left( { - 2} \right)^{ - 2}}{.64^{{2 \over 3}}} - {8^{ - 1{1 \over 3}}}\) \( + {\left( {{9^0}} \right)^2};\) Lời giải chi tiết: \(0,{001^{{{ - 1} \over 3}}} - {\left( { - 2} \right)^{ - 2}}{.64^{{2 \over 3}}} - {8^{ - 1{1 \over 3}}} + {\left( {{9^0}} \right)^2} \) \(= {\left( {{{10}^{ - 3}}} \right)^{ - {1 \over 3}}} - {2^{ - 2}}.{\left( {{2^6}} \right)^{{2 \over 3}}} - {\left( {{2^3}} \right)^{ - {4 \over 3}}} + 1\) \( = 10 - {2^2} - {2^{ - 4}} + 1 = 7 - {1 \over {16}} = {{111} \over {16}}\) Cách khác: LG c \({27^{{2 \over 3}}} + {\left( {{1 \over {16}}} \right)^{ - 0,75}} - {25^{0,5}}\) Lời giải chi tiết: \({27^{{2 \over 3}}} + {\left( {{1 \over {16}}} \right)^{ - 0,75}} - {25^{0,5}} \) \(= {\left( {{3^3}} \right)^{{2 \over 3}}} + {\left( {{2^{ - 4}}} \right)^{ - {3 \over 4}}} - {\left( {{5^2}} \right)^{{1 \over 2}}} \) \(= {3^2} + {2^3} - 5 = 12\) Cách khác: LG d \({\left( { - 0,5} \right)^{ - 4}} - {625^{0,25}} - {\left( {2{1 \over 4}} \right)^{ - 1{1 \over 2}}} \) \(+ 19{\left( { - 3} \right)^{ - 3}}\) Lời giải chi tiết: \({\left( { - 0,5} \right)^{ - 4}} - {625^{0,25}} - {\left( {2{1 \over 4}} \right)^{ - 1{1 \over 2}}} \) \(+ 19{\left( { - 3} \right)^{ - 3}} \) \(= {\left( {{{\left( { - 2} \right)}^{ - 1}}} \right)^{ - 4}} - {\left( {{5^4}} \right)^{{1 \over 4}}} - {\left( {{{\left( {{3 \over 2}} \right)}^2}} \right)^{ - {3 \over 2}}} \) \(+ {{19} \over { - 27}}\) \( = {2^4} - 5 - {\left( {{3 \over 2}} \right)^{ - 3}} - {{19} \over {27}} \) \(= 11 - {8 \over {27}} - {{19} \over {27}} = 10.\) Cách khác:
HocTot.XYZ
|