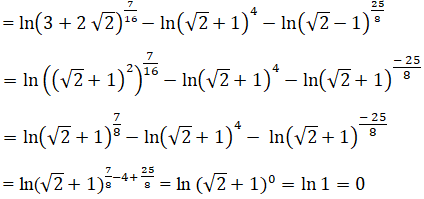Bài 44 trang 97 SGK Đại số và Giải tích 12 Nâng caoChứng minh: Đề bài Chứng minh: \({7 \over {16}}\ln \left( {3 + 2\sqrt 2 } \right) - 4\ln \left( {\sqrt 2 + 1} \right) - {{25} \over 8}\ln \left( {\sqrt 2 - 1} \right) = 0\) Lời giải chi tiết Ta có: \(\begin{array}{l} Do đó, \({7 \over {16}}\ln \left( {3 + 2\sqrt 2 } \right) - 4\ln \left( {\sqrt 2 + 1} \right) - {{25} \over 8}\ln \left( {\sqrt 2 - 1} \right)\) \( = {7 \over {16}}\ln {\left( {\sqrt 2 + 1} \right)^2} - 4\ln \left( {\sqrt 2 + 1} \right) - {{25} \over 8}\ln {(\sqrt 2 + 1)^{-1} }\) \( = \frac{7}{{16}}.2\ln \left( {\sqrt 2 + 1} \right) - 4\ln \left( {\sqrt 2 + 1} \right) - \frac{{25}}{8}.\left( { - \ln \left( {\sqrt 2 + 1} \right)} \right)\) \( = {7 \over 8}\ln \left( {\sqrt 2 + 1} \right) - 4\ln \left( {\sqrt 2 + 1} \right) + {{25} \over 8}\ln \left( {\sqrt 2 + 1} \right) = 0\) Cách trình bày khác:
HocTot.XYZ
|