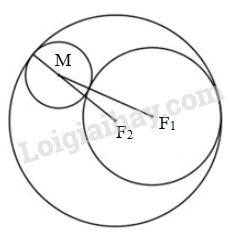
Giải bài 5 trang 88 SGK Hình học 10Cho hai đường tròn Đề bài Cho hai đường tròn \({C_1}({F_1};{R_1})\) và \({C_2}({F_2};{R_2})\). \(C_1\) nằm trong \(C_2\) và \(F_1≠ F_2\). Đường tròn \((C)\) thay đổi luôn tiếp xúc ngoài với \(C_1\) và tiếp xúc trong với \(C_2\).Hãy chứng tỏ rằng tâm \(M\) của đường tròn \((C)\) di động trên một elip. Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Tính \(MF_1,MF_2\) theo các bán kính, chú ý điều kiện tiếp xúc ngoài, tiếp xúc trong. - Tính \(MF_1+MF_2\) và sử dụng định nghĩa elip để suy ra đpcm. Lời giải chi tiết
Gọi \(R\) là bán kính của đường tròn \((C)\) \((C)\) và \(C_1\) tiếp xúc ngoài với nhau \( \Rightarrow \)\(MF_1= R_1+ R\) (1) \((C)\) và \(C_2\) tiếp xúc trong với nhau \( \Rightarrow \)\(MF_2= R_2- R\) (2) Từ (1) và (2) ta được \(M{F_1} + M{F_2} = ({R_1}+R) + ({R_2}-R) \) \(=R_1+R_2\) không đổi. Điểm M có tổng các khoảng cách \(M{F_1} + M{F_2} \) đến hai điểm cố định \(F_1\) và \(F_2\) bằng một độ dài không đổi \({R_1} + {R_2}.\) Vậy tập hợp điểm \(M\) là đường elip, có các tiêu điểm \(F_1\) và \(F_2\) và có tiêu cự \(F_1F_2= R_1+R_2.\) HocTot.XYZ
|