Bài 62 trang 57 SGK giải tích 12 nâng caoa) Khảo sát sự biến thiên và vẽ đồ thị hàm số: b) Chứng minh rằng giao điểm I của hai đường tiệm cận của đường cong đã cho là tâm đối xứng của nó.
Lựa chọn câu để xem lời giải nhanh hơn
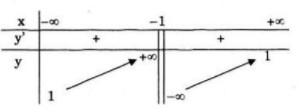
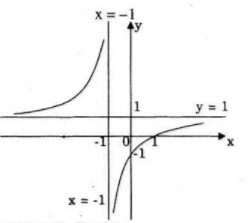
LG a Khảo sát sự biến thiên và vẽ đồ thị hàm số: \(y = {{x - 1} \over {x + 1}}\) Lời giải chi tiết: Tập xác định: \(D = R\backslash \left\{ { - 1} \right\}\) Sự biến thiên: \(y' = {2 \over {{{(x + 1)}^2}}} > 0\,\forall x \in D\) Hàm số đồng biến trên khoảng \(( - \infty ; - 1)\) và \(( - 1; + \infty )\) Giới hạn: \(\mathop {\lim y}\limits_{x \to - {1^ - }} = + \infty ;\,\mathop {\lim y}\limits_{x \to - {1^ + }} = - \infty \) Tiệm cận đứng: \(x=-1\) \(\mathop {\lim y}\limits_{x \to \pm \infty } = 1\) Tiệm cận ngang: \(y=1\) Bảng biến thiên:
Đồ thị giao \(Ox\) tại điểm \((1;0)\) Đồ thị giao \(Oy\) tại điểm \((0;-1)\)
LG b Chứng minh rằng giao điểm \(I\) của hai đường tiệm cận của đường cong đã cho là tâm đối xứng của nó. Lời giải chi tiết: Giao điểm của hai tiệm cận của đường cong là \(I(-1;1)\) Công thức đổi trục tọa độ theo vecto \(\overrightarrow {OI} \) là \(\left\{ \matrix{ Phương trình đường cong trong hệ tọa độ \(IXY\) là: \(Y + 1 = {{X - 1 - 1} \over {X - 1 + 1}} \) \(\Leftrightarrow Y + 1 = {{X - 2} \over X} =1-{2\over X}\) \(\Leftrightarrow Y = - {2 \over X}\) Đây là hàm số lẻ nên đồ thị nhận gốc \(I\) làm tâm đối xứng. HocTot.XYZ
|