Bài 65 trang 58 sách giải tích 12 nâng caoa) Khảo sát sự biến thiên và vẽ đồ thị của hàm số: b) Với các giá trị nào t=của m đường thẳng y = m – x cắt đồ thị hàm số đã cho tại hao điểm phân biệt? c) Gọi A và B là hai giao điểm đó. Tìm tập hợp các trung điểm của đoạn thẳng AB khi m biến thiên.
Lựa chọn câu để xem lời giải nhanh hơn
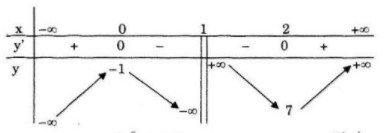
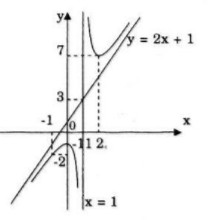
LG a Khảo sát sự biến thiên và vẽ đồ thị của hàm số: \(y = {{2{x^2} - x + 1} \over {x - 1}}\) Lời giải chi tiết: Tập xác định: \(D = \mathbb R\backslash \left\{ 1 \right\}\) Sự biến thiên: \(\eqalign{ Hàm số đồng biến trên khoảng \(( - \infty ;0)\) và \((2; + \infty )\) Hàm số nghịch biến trên khoảng \((0;1)\) và \((1;2)\) Cực trị Hàm số đạt cực đại tại \(x=0\), \(y_{CĐ}=1\) Hàm số đạt cực tiểu tại \(x=2\), \(y_{CT}=7\) Giới hạn: \(\mathop {\lim y}\limits_{x \to {1^ - }} = - \infty ;\,\mathop {\lim y}\limits_{x \to {1^ + }} = + \infty \) Tiệm cận đứng là: \(x=1\) \(\eqalign{ Tiệm cận xiên là: \(y=2x+1\) Bảng biến thiên:
Đồ thị cắt \(Oy\) tại điểm \((0;-1)\)
LG b Với các giá trị nào của m đường thẳng \(y = m – x\) cắt đồ thị hàm số đã cho tại hai điểm phân biệt? Lời giải chi tiết: Hoành độ giao điểm của đường thẳng và đường cong đã cho là nghiệm của phương trình \(\eqalign{ Đường thẳng cắt đường cong tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác 1 \(\begin{array}{l} \(\Leftrightarrow m < 4 - 2\sqrt 6 \,\,\text{hoặc}\,\,m > 4 + 2\sqrt {6\,\,} \,\left( 2 \right)\) LG c Gọi \(A\) và \(B\) là hai giao điểm đó. Tìm tập hợp các trung điểm của đoạn thẳng \(AB\) khi \(m\) biến thiên. Lời giải chi tiết: Hoành độ giao điểm \(A, B\) là các nghiệm của (1) Hoành độ trung điểm \(M\) của \(AB\) là: \({x_M} = {1 \over 2}\left( {{x_A} + {x_B}} \right) = {{m + 2} \over 6}\) Vì M nằm trên đường thẳng y = m – x nên \({y_M} = m - {x_M} = m - {{m + 2} \over 6} = {{5m - 2} \over 6}\) Khử \(m\) từ hệ \(\left\{ \matrix{ \(\begin{array}{l} Vậy \(M\) nằm trên đường thẳng \(y = 5x -2\) Vì \(m\) chỉ lấy giá trị thỏa mãn (2) nên: \(m < 4 - 2\sqrt 6 \) \(\Rightarrow m = 6{x_M} - 2 < 4 - 2\sqrt 6 \) \( \Leftrightarrow 6{x_M} < 6 - 2\sqrt 6 \) \(\Rightarrow {x_M} < 1 - {{\sqrt 6 } \over 3}\) \(m > 4 + 2\sqrt 6 \) \(\Rightarrow m = 6{x_M} - 2 > 4 + 2\sqrt 6 \) \( \Leftrightarrow 6{x_M} > 6 + 2\sqrt 6 \) \(\Rightarrow {x_M} > 1 + {{\sqrt 6 } \over 3}\) Vậy tập hợp các trung điểm \(M\) của đoạn \(AB\) là phần của đường thẳng \(y = 5x -2\) với \({x_M} < 1 - {{\sqrt 6 } \over 3}\) hoặc \({x_M} > 1 + {{\sqrt 6 } \over 3}\) HocTot.XYZ
|