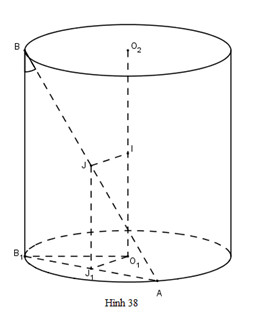
Giải bài 7 trang 39 SGK Hình học lớp 12Một hình trụ có bán kính r và chiều cao h = r√3. Video hướng dẫn giải Một hình trụ có bán kính \(r\) và chiều cao \(h = r\sqrt3\). LG a a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ. Phương pháp giải: Áp dụng công thức: \({S_{xq}} = 2\pi rh,\,\,{S_{tp}} = 2\pi rh + \pi {r^2}\) với \(r;h\) lần lượt là bán kính đáy và độ dài đường cao của hình trụ. Lời giải chi tiết:
Theo công thức ta có: \(S_{xq} = 2πrh = 2\sqrt3 πr^2\) \(S_{tp} = 2πrh + 2πr^2 = 2\sqrt3 πr^2 + 2 πr^2 \) \(= 2(\sqrt3 + 1)πr^2\) ( đơn vị thể tích) LG b b) Tính thể tích khối trụ tạo nên bởi hình trụ đã cho. Phương pháp giải: Áp dụng công thức: \(V = \pi {r^2}h\). Lời giải chi tiết: \(V\)trụ = \(πR^2h = \sqrt3 π r^3\) LG c c) Cho hai điểm \(A\) và \(B\) lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng \(AB\) và trục của hình trụ bằng \(30^0\). Tính khoảng cách giữa đường thẳng \(AB\) và trục của hình trụ. Phương pháp giải: +) Giả sử trục của hình trụ là \(O_1O_2\) và \(A\) nằm trên đường tròn tâm \(O_1\), \(B\) nằm trên đường tròn tâm \(O_2\). Kẻ \(BB_1\) // \({O_1}{O_2}\) \( \Rightarrow \widehat {\left( {AB;{O_1}{O_2}} \right)} = \widehat {\left( {AB;B{B_1}} \right)} = \widehat {AB{B_1}}\). +) Xác định khoảng cách giữa AB và \({O_1}{O_2}\) bằng cách xác định đường vuông góc chung giữa hai đường thẳng đó. Lời giải chi tiết: Giả sử trục của hình trụ là \(O_1O_2\) và \(A\) nằm trên đường tròn tâm \(O_1\), \(B\) nằm trên đường tròn tâm \(O_2\); \(I\) là trung điểm của \(O_1O_2\) , \(J\) là trung điểm của \(AB\). Ta chứng minh \(IJ\) là đường vuông góc chung của \(O_1O_2\) và \(AB\). Hạ \(BB_1\) vuông góc với đáy, \(J_1\) là hình chiếu vuông góc của \(J\) xuống đáy. Dễ thấy \(J_1\) là trung điểm của \(AB_1\) (định lí đường trung bình của tam giác). Ta có: \(\left\{ \begin{array}{l}{O_1}{J_1} \bot A{B_1}\\{O_1}{J_1} \bot B{B_1}\end{array} \right. \Rightarrow {O_1}{J_1} \bot \left( {AB{B_1}} \right)\). Mà \(IJ//{O_1}{J_1} \Rightarrow IJ \bot \left( {AB{B_1}} \right)\) \( \Rightarrow IJ \bot AB\). \(\left\{ \begin{array}{l}IJ//{O_1}{J_1}\\{O_1}{O_2} \bot {O_1}{J_1}\end{array} \right. \Rightarrow IJ \bot {O_1}{O_2}\). Vậy IJ là đường vuông góc chung của \(O_1O_2\) và \(AB\) \( \Rightarrow d\left( {AB;{O_1}{O_2}} \right) = IJ\) Ta có: \(BB_1\) // \({O_1}{O_2}\) \( \Rightarrow \widehat {\left( {AB;{O_1}{O_2}} \right)} = \widehat {\left( {AB;B{B_1}} \right)} = \widehat {AB{B_1}}\). do vậy: \(AB_1 = BB_1.tan 30^0\) = \( \frac{\sqrt{3}}{3}h = r\). Xét tam giác vuông \(O_1J_1A\) vuông tại \(J_1\) ta có: \( O_{1}J^{2}_{1}\) = \( O_{1}A^{2}\) - \( AJ^{2}_{1} =\) \( r^{2} - {\left( {{r \over 2}} \right)^2}=\) \( \frac{3}{4}r^{2}\) \( \Rightarrow {O_1}{J_1} = \frac{{r\sqrt 3 }}{2}\) Vậy khoảng cách giữa \(AB\) và \(O_1O_2\) là: \( \frac{\sqrt{3}}{2}r\). HocTot.XYZ
|