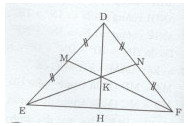
Bài 8 trang 176 Tài liệu dạy – học Toán 7 tập 1Giải bài tập Cho tam giác DEF cân tại D. Gọi M là trung điểm của DE, N là trung điểm của DF. Đề bài Cho tam giác DEF cân tại D. Gọi M là trung điểm của DE, N là trung điểm của DF. a) Chứng minh rằng EN = FM. b) Gọi K là giao điểm của EN với FM. Chưng sminh rằng tam giác KEF cân. c) Chứng minh rằng DK là phân giác \(\widehat {EDF}\) d) DK cắt EF tại H. Biết DE = 10 cm, EF = 12 cm. Tính DH. Lời giải chi tiết a)Ta có: \(DM = ME = {{DE} \over 2}\) (M là trung điểm của DE) \(DN = NF = {{DF} \over 2}\) (N là trung điểm của DF) Mà DE = DF (tam giác DEF cân tại D) Do đó: DM = ME = DN = NF. Xét tam giác DEN và DFM ta có: DN = DM (chứng minh trên) \(\widehat {EDN} = \widehat {FDN}\) (góc chung) DE = DF (tam giác DEF cân tại D) Do đó: \(\Delta DEN = \Delta DFM(c.g.c) \Rightarrow EN = FM.\) b) Ta có: \(\widehat {DEF} = \widehat {DFE}(\Delta DEF\) cân tại D) \(\Rightarrow \widehat {DEN} + \widehat {KEF} = \widehat {DFM} + \widehat {KFE}\) Mà \(\widehat {DEN} = \widehat {DFM}(\Delta DEN = \Delta DFM)\) . Do đó: \(\widehat {KEF} = \widehat {KFE}.\) Vậy tam giác KEF cân tại K. c) Xét tam giác DEK và DFK ta có: DE = DF (tam giác DEF cân tại D) \(\widehat {DEK} = \widehat {DFK}(\Delta DEN = \Delta DFM)\) EK = FK (chứng minh câu b) Do đó: \(\Delta DEK = \Delta DFK(c.g.c) \Rightarrow \widehat {EDK} = \widehat {FDK}.\) Vậy DK là tia phân giác của góc EDF. d) Xét tam giác DHE và DHF ta có: DH là cạnh chung DE = DF (tam giác DEF cân tại D) \(\widehat {EDH} = \widehat {FDH}\) (chứng minh câu c) Do đó: \(\Delta DHE = \Delta DHF(c.g.c) \Rightarrow \widehat {DHE} = \widehat {DHF}\) Mà \(\widehat {DHE} + \widehat {DHF} = {180^0}\) (kề bù) Nên \(\widehat {DHE} + \widehat {DHE} = {180^0} \Rightarrow 2\widehat {DHE} = {180^0} \Rightarrow \widehat {DHE} = {90^0}.\) Ta có: \(EH = HF = {{EF} \over 2} = {{12} \over 2} = 6cm(\Delta DHE = \Delta DHF)\) Tam giác HDE vuông tại H: \(D{E^2} = D{H^2} + E{H^2}\) (định lí Pythagore) Do đó: \(D{H^2} = D{E^2} - E{H^2} = {10^2} - {6^2} = 100 - 36 = 64\) Mà DH > 0. Vậy \(DH = \sqrt {64} = 8(cm).\) HocTot.XYZ
|