Bài 8 trang 45 SGK Hình học 12 Nâng caoCho tứ diện ABCD với AB = CD = c, AC = BD = b, AD = BC = a. a) Tính diện tích mặt cầu ngoại tiếp tứ diện. b) Chứng minh rằng có một mặt cầu tiếp xúc với bốn mặt của hình tứ diện (nó được gọi là mặt cầu nội tiếp tứ diện)
Lựa chọn câu để xem lời giải nhanh hơn
Cho tứ diện ABCD với AB = CD = c, AC = BD = b, AD = BC = a. LG a Tính diện tích mặt cầu ngoại tiếp tứ diện. Lời giải chi tiết:
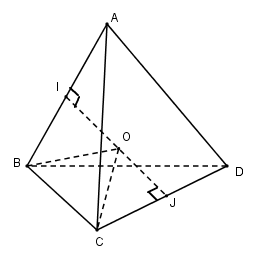
Gọi I và J lần lượt là trung điểm của AB và CD. Ta có \(\Delta ABC = \Delta BAD\,\,\left( {c.c.c} \right) \) \(\Rightarrow CI = DI\)(2 trung tuyến tương ứng) \(\Delta CID\) cân tại I nên \(IJ \bot CD\). Do ∆CAD = ∆DBC (c.c.c) nên AJ = BJ hay tam giác ABJ cân tại J. Lại có CJ là đường trung tuyến nên đồng thời là đường cao. ⇒ IJ ⊥ AB Gọi O là trung điểm của IJ thì OA = OB và OC = OD. Vì AB = CD = c nên hai tam giác vuông OIB và OJC bằng nhau, do đó OB = OC. Vậy O cách đều bốn đỉnh A, B, C, D. Mặt cầu ngoại tiếp tứ diện ABCD có tâm R = OA. Ta có: \(O{A^2} = O{I^2} + A{I^2} \) \(= {{I{J^2}} \over 4} + {{A{B^2}} \over 4} \) \(= {{I{J^2} + {c^2}} \over 4}\) Vì CI là trung tuyến của tam giác ABC nên \(C{I^2} = {{2{a^2} + 2{b^2} - {c^2}} \over 4}\) Suy ra \(I{J^2} = C{I^2} - C{J^2} \) \(= {{2{a^2} + 2{b^2} - {c^2}} \over 4} - {{{c^2}} \over 4} = {{{a^2} + {b^2} - {c^2}} \over 2}\) Như vậy \({R^2} = O{A^2} = {{{a^2} + {b^2} + {c^2}} \over 8}\) và diện tích mặt cầu ngoại tiếp tứ diện ABCD là: \(S = 4\pi {R^2} = {\pi \over 2}\left( {{a^2} + {b^2} + {c^2}} \right)\) LG b Chứng minh rằng có một mặt cầu tiếp xúc với bốn mặt của hình tứ diện (nó được gọi là mặt cầu nội tiếp tứ diện) Lời giải chi tiết:
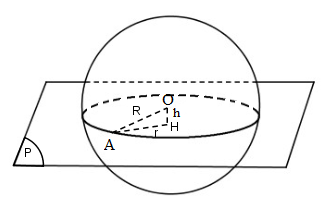
Các mặt của hình tứ diện là các tam giác bằng nhau (đều có ba cạnh bằng a, b, c) nên các đường tròn ngoại tiếp các tam giác đó có bán kính r bằng nhau. Các đường tròn đó đều nằm trên mặt cầu tâm (O;R) nên khoảng cách từ tâm O tới các mặt phẳng chứa các đường tròn đó bằng nhau và bằng \(h = \sqrt {{R^2} - {r^2}} \). Vậy mặt cầu tâm O, bán kính h là mặt cầu nội tiếp tứ diện ABCD. (OA = R, OH = h, HA = r) HocTot.XYZ
|