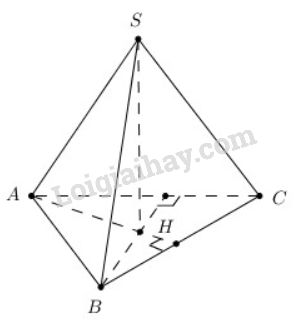
Bài 9 trang 114 SGK Hình học 11Cho hình chóp tam giác đều S.ABC... Đề bài Cho hình chóp tam giác đều \(S.ABC \) có \(SH\) là đường cao. Chứng minh \(SA ⊥ BC\) và \(SB ⊥ AC\). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Chứng minh \(BC \bot \left( {SAH} \right);\,\,AC \bot \left( {SBH} \right)\). Lời giải chi tiết
Hình chóp tam giác đều nên ta có \(H\) là tâm của tam giác đều \(ABC\) \(SH ⊥ (ABC) \Rightarrow SH ⊥ BC\) Và \(AH ⊥ BC\) (vì \(H\) là trực tâm) Suy ra \( BC ⊥ (SAH)\) \(SA\subset (SAH)\Rightarrow BC ⊥ SA\). Chứng minh tương tự, ta có: \(SH \, \bot \, \left( {ABC} \right) \Rightarrow SH \, \bot \, AC\). Mà \(H\) là trực tâm của tam giác \(ABC\) \( \Rightarrow BH \, \bot \, AC\) \( \Rightarrow AC \, \bot \, \left( {SBH} \right);\,\,SB \subset \left( {SBH} \right) \) \(\Rightarrow AC \, \bot \, SB\) Cách khác: Sử dụng định lí ba đường vuông góc + Ta có: \(AH ⊥ BC\) Mà \(AH\) là hình chiếu của \(SA\) trên \((ABC)\) \(⇒ BC ⊥ SA\) ( định lí ba đường vuông góc) + Lại có : \(AC ⊥ BH.\) \(BH\) là hình chiếu của \(SB\) trên \((ABC)\) \(⇒ AC ⊥ SB\) ( định lí ba đường vuông góc) HocTot.XYZ
|