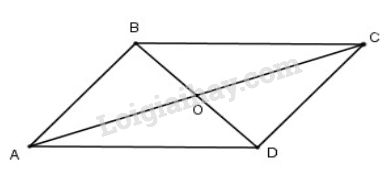
Bài 9 trang 59 SGK Hình học 10Cho hình bình hành ABCD có Đề bài Cho hình bình hành \(ABCD\) có \(AB = a, BC = b ,BD = m\), và \(AC = n\). Chứng minh rằng : $${m^2} + {n^2} = 2({a^2} + {b^2})$$ Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Công thức đường trung tuyến: \( m_a^2=\frac{2(b^2+c^2)-a^2}{4}.\) Lời giải chi tiết
Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và BD. Tam giác ABD có AO là đường trung tuyến. Áp dụng định lí về đường trung tuyến: \(A{O^2} = \frac{{2\left( {A{B^2} + A{D^2}} \right) - B{D^2}}}{4}\) Mà O là trung điểm AC nên \(AO = \frac{{AC}}{2} = \frac{n}{2}\) Thay \(OA = \frac{n}{2}, \, AB = a,\) \(AD = BC = b\) và \(BD = m\) ta được: \(\begin{array}{l} Cách 2: Áp dụng định lý đường trung tuyến cho tam giác ABC có BO là đường trung tuyến ra có: \(\begin{array}{l} Cách 3: Áp dụng định lí cô sin cho tam giác ABC có: \(\begin{array}{l} Áp dụng định lí cô sin cho tam giác ABD có: \(\begin{array}{l} \(\begin{array}{l} Mà \(\widehat {ABC} + \widehat {BAD} = {{180}^0} \) \( \Rightarrow \cos \widehat {ABC} = - \cos \left( {{{180}^0} - \widehat {ABC}} \right) \) \(= - \cos \widehat {BAD}\) \( \Rightarrow \cos \widehat {ABC} + \cos \widehat {BAD} = 0\) Vậy \({m^2} + {n^2} = 2\left( {{a^2} + {b^2}} \right)\). HocTot.XYZ
|