Nội dung từ Loigiaihay.Com
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.
-
A.
$m < - \dfrac{1}{3}$
-
B.
$m \leqslant - \dfrac{1}{3}$
-
C.
$m \leqslant - \dfrac{4}{3}$
-
D.
$m \leqslant 0$
- Bước 1: Nêu điều kiện để hàm số đơn điệu trên $D$:
+ Hàm số $y = f\left( x \right)$ đồng biến trên $D \Leftrightarrow y' = f'\left( x \right) \geqslant 0,\forall x \in D$.
+ Hàm số $y = f\left( x \right)$ nghịch biến trên $D \Leftrightarrow y' = f'\left( x \right) \leqslant 0,\forall x \in D$.
- Bước 2: Từ điều kiện trên sử dụng các cách suy luận khác nhau cho từng bài toán để tìm $m$.
Chú ý: Dưới đây là một trong những cách hay được sử dụng:
- Rút $m$ theo $x$ sẽ xảy ra một trong hai trường hợp: $m \geqslant g\left( x \right),\forall x \in D$ hoặc $m \leqslant g\left( x \right),\forall x \in D$.
- Khảo sát tính đơn điệu của hàm số $y = g\left( x \right)$ trên $D$.
- Kết luận: Đánh giá $g(x)$ suy ra giá trị của $m$.
- Bước 3: Kết luận.
Ta có: $y' = {x^2} - 4mx + 4m$.
Hàm số nghịch biến trên $\left( { - 2;0} \right) \Rightarrow y' \leqslant 0,\forall x \in \left( { - 2;0} \right)$
$\Leftrightarrow {x^2} - 4mx + 4m \leqslant 0,\forall x \in \left( { - 2;0} \right)$ $ \Leftrightarrow {x^2} - 4m\left( {x - 1} \right) \leqslant 0$
$\Leftrightarrow 4m\left( {x - 1} \right) \geqslant {x^2} \Leftrightarrow 4m \leqslant \dfrac{{{x^2}}}{{x- 1}}$ (vì $ - 2 < x < 0$).
Xét hàm $g\left( x \right) = \dfrac{{{x^2}}}{{x - 1}}$ trên $\left( { - 2;0} \right)$ ta có:
$g'\left( x \right) = \dfrac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \notin \left( { - 2;0} \right) \hfill \\x = 2 \notin \left( { - 2;0} \right) \hfill \\ \end{gathered} \right. $
$\Rightarrow g'\left( x \right) > 0,\forall x \in \left( { - 2;0} \right)$.
Do đó hàm số $y = g\left( x \right)$ đồng biến trên $\left( { - 2;0} \right)$.
Suy ra \(g\left( { - 2} \right) < g\left( x \right) < g\left( 0 \right),\forall x \in \left( { - 2;0} \right)\) hay \( - \dfrac{4}{3} < g\left( x \right) < 0,\forall x \in \left( { - 2;0} \right)\).
Khi đó \(4m \le g\left( x \right),\forall x \in \left( { - 2;0} \right) \Leftrightarrow 4m \le - \dfrac{4}{3} \Leftrightarrow m \le - \dfrac{1}{3}\).
Vậy $m \leqslant - \dfrac{1}{3}$.
Đáp án : B
HS thường nhầm lẫn ở bước kết luận giá trị cần tìm của $m$, khi tìm được $g\left( x \right) > g\left( { - 2} \right) = - \dfrac{4}{3}; g\left( x \right) < g\left( 0 \right) = 0$, nhiều em vội vàng kết luận $m \leqslant - \dfrac{4}{3}$ dẫn đến chọn nhầm đáp án C, một số em khác thì nhớ sai điều kiện, cho rằng $4m \leqslant 0 \Leftrightarrow m \leqslant 0$ và chọn nhầm đáp án D.

Các bài tập cùng chuyên đề
Bài 1 :
Hình dưới là đồ thị hàm số \(y = f'\left( x \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
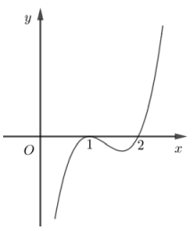
-
A.
\(\left( {0;1} \right)\) và \(\left( {2; + \infty } \right)\)
-
B.
\(\left( {1;2} \right)\)
-
C.
\(\left( {2; + \infty } \right)\)
-
D.
\(\left( {0;1} \right)\)
Bài 2 :
Trong tất cả các giá trị của tham số $m$ để hàm số $y = \dfrac{1}{3}{x^3} + m{x^2} - mx - m$ đồng biến trên $R$, giá trị nhỏ nhất của $m$ là:
-
A.
$ - 4$
-
B.
$ - 1$
-
C.
$0$
-
D.
$1$
Bài 3 :
Cho bảng biến thiên hình bên, hàm số nghịch biến trên:
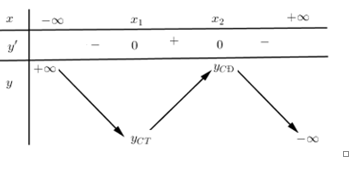
-
A.
$\left( {{x_1};{x_2}} \right)$
-
B.
$\left( { - \infty ;{x_1}} \right)$
-
C.
$\left( {{x_1}; + \infty } \right)$
-
D.
$\left( { - \infty ;{x_2}} \right)$
Bài 4 :
Hình bên là đồ thị hàm số \(y = f'\left( x \right)\) Hỏi hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?
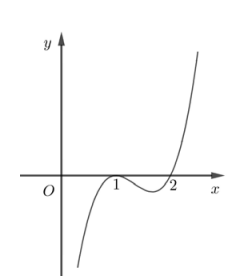
-
A.
\(\left( {2;3} \right)\)
-
B.
\(\left( {1; + \infty } \right)\)
-
C.
\(\left( {2; + \infty } \right)\)
-
D.
\(\left( { - \infty ;2} \right)\)
Bài 5 :
Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = mx - \sin x$ đồng biến trên $\mathbb{R}.$
-
A.
$m > 1.$
-
B.
$m \le - 1.$
-
C.
$m \ge 1.$
-
D.
$m \ge - 1.$
Bài 6 :
Tìm tất cả các giá trị của tham số m để hàm số $y = {x^3} + {x^2} + mx + 1$ đồng biến trên khoảng $\left( { - \infty ; + \infty } \right)$
-
A.
$m \geqslant \dfrac{4}{3}$
-
B.
$m \leqslant \dfrac{4}{3}$
-
C.
$m \geqslant \dfrac{1}{3}$
-
D.
$m \leqslant \dfrac{1}{3}$
Bài 7 :
Tập hợp tất cả các giá trị của m để hàm số $y = \dfrac{1}{3}{x^3} - \left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x - 2$ luôn tăng trên $R$
-
A.
$m > 1$
-
B.
$\left[ {\begin{array}{*{20}{l}}{m < 1}\\{m > 3}\end{array}} \right.$
-
C.
$2 \le m \le 3$
-
D.
$1 \le m \le 3$
Bài 8 :
Tìm $m$ để hàm số $y = {x^3} - 3{x^2} + mx + 2$ tăng trên khoảng $\left( {1; + \infty {\rm{\;}}} \right).$
-
A.
$m \ge 3.$
-
B.
$m \ne 3.$
-
C.
$m \le 3.$
-
D.
$m < 3.$
Bài 9 :
Hàm số $y = {x^3} - 6{x^2} + mx + 1$ đồng biến trên $\left( {0; + \infty {\rm{\;}}} \right)$ khi giá trị của $m$ là:
-
A.
$m \ge 12$
-
B.
$m \le 12$
-
C.
$m \ge 0$
-
D.
$m \le 0$
Bài 10 :
Tìm các giá trị của tham số $m$ để hàm số $y = - {\mkern 1mu} {x^3} + m{x^2} - m$ đồng biến trên khoảng $\left( {1;2} \right).$
-
A.
$\left( {\dfrac{3}{2};3} \right).$
-
B.
$\left( { - {\mkern 1mu} \infty ;\dfrac{3}{2}} \right).$
-
C.
$\left[ {3; + {\mkern 1mu} \infty } \right).$
-
D.
$\left( { - {\mkern 1mu} \infty ;3} \right].$
Bài 11 :
Cho bảng biến thiên hình bên, hàm số đồng biến trên:
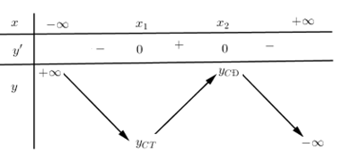
-
A.
\(\left( {{x_1};{x_2}} \right)\)
-
B.
\(\left( { - \infty ;{x_1}} \right)\)
-
C.
\(\left( {{x_1}; + \infty } \right)\)
-
D.
\(\left( { - \infty ;{x_2}} \right)\)
Bài 12 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

-
A.
\(\left( {0;1} \right)\)
-
B.
\(\left( { - \infty ; - 1} \right)\)
-
C.
\(\left( { - 1;1} \right)\)
-
D.
\(\left( { - 1;0} \right)\)
Bài 13 :
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = - {x^3} - 6{x^2} + \left( {4m - 9} \right)x + 4\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\) là:
-
A.
\(\left( { - \infty ;0} \right]\)
-
B.
\(\left[ { - \dfrac{3}{4}; + \infty } \right)\)
-
C.
\(\left( { - \infty ; - \dfrac{3}{4}} \right]\)
-
D.
\(\left[ {0; + \infty } \right)\)
Bài 14 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào trong các khoảng sau?
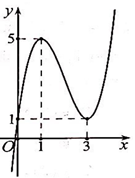
-
A.
\(\left( {0;1} \right)\).
-
B.
\(\left( {1;5} \right)\).
-
C.
\(\left( {3; + \infty } \right)\).
-
D.
\(\left( {1;2} \right)\).
Bài 15 :
Tập tất cả giá trị của tham số \(m\) để hàm số \(y = {x^3} - 3m{x^2} + 3x + 1\) đồng biến trên \(\mathbb{R}\) là
-
A.
\(\left[ { - 1;\,1} \right]\).
-
B.
\(m \in \left( { - \infty ;\, - 1} \right] \cup \left[ {1;\, + \infty } \right)\).
-
C.
\(\left( { - \infty ;\, - 1} \right) \cup \left( {1;\, + \infty } \right)\).
-
D.
\(\left( { - 1;\,1} \right)\).
Bài 16 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
Hàm số đã cho nghịch biến trên khoảng:
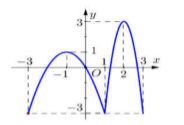
-
A.
\(\left( {0;\,\,2} \right)\)
-
B.
\(\left( { - 2;\,0} \right)\)
-
C.
\(\left( { - 3; - 1} \right)\)
-
D.
\(\left( {2;\,3} \right)\)
Bài 17 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:

Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng
-
A.
\(\left( {1;2} \right)\)
-
B.
\(\left( {2;3} \right)\)
-
C.
\(\left( { - 1;0} \right)\)
-
D.
\(\left( { - 1;1} \right)\)
Bài 18 :
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu \(f'\left( x \right)\) như sau:

Hàm số \(y = f\left( {2 - 3x} \right)\) đồng biến trên khoảng nào sau đây?
-
A.
\(\left( {1;3} \right)\)
-
B.
\(\left( {1;2} \right)\)
-
C.
\(\left( {2;3} \right)\)
-
D.
\(\left( {0;1} \right)\)
Bài 19 :
Tập tất cả các giá trị của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} + 2{x^2} - mx\) đồng biến trên \(\mathbb{R}\) là:
-
A.
\(\left( { - 4; + \infty } \right)\)
-
B.
\(\left[ { - 4; + \infty } \right)\)
-
C.
\(\left( { - \infty ; - 4} \right)\)
-
D.
\(\left( { - \infty ; - 4} \right]\)
Bài 20 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Hàm số đã cho nghịch biến trên khoảng:
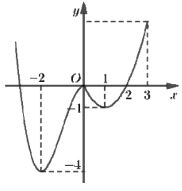
-
A.
\(\left( { - 1;\,\,0} \right)\)
-
B.
\(\left( { - 2; - 1} \right)\)
-
C.
\(\left( {0;\,\,1} \right)\)
-
D.
\(\left( {1;\,\,3} \right)\)
Bài 21 :
Đề thi THPT QG - 2021 - mã 101
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( {0;1} \right)\)
-
B.
\(\left( { - \infty ;0} \right)\)
-
C.
\(\left( {0; + \infty } \right)\)
-
D.
\(\left( { - 1;1} \right)\)
Bài 22 :
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
A.
\(\left( { - \infty ;2} \right)\)
-
B.
\(\left( {0;2} \right)\)
-
C.
\(\left( { - 2;2} \right)\)
-
D.
\(\left( {2; + \infty } \right)\)
Bài 23 :
Đề thi THPT QG - 2021 - mã 102
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
-
A.
\(\left( { - 1;1} \right)\)
-
B.
\(\left( { - \infty ;0} \right)\)
-
C.
\(\left( {0;1} \right)\)
-
D.
\(\left( {0; + \infty } \right)\)
Bài 24 :
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( { - 1;1} \right)\)
-
B.
\(\left( {1; + \infty } \right)\)
-
C.
\(\left( { - \infty ;1} \right)\)
-
D.
\(\left( {0;3} \right)\)
Bài 25 :
Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = {x^3} - 3\left( {2m + 1} \right){x^2} + \left( {12m + 5} \right)x + 2\) đồng biến trên khoảng \(\left( {2; + \infty } \right).\) Số phần tử của \(S\) bằng:
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(0\)
Bài 26 :
Quan sát đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\) (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:
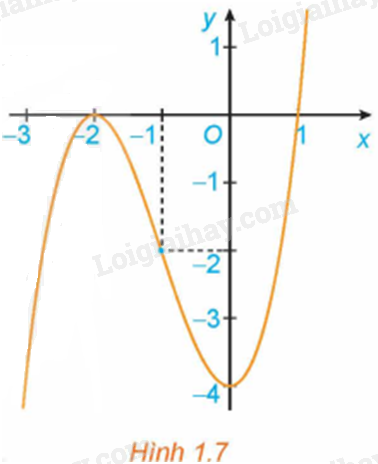
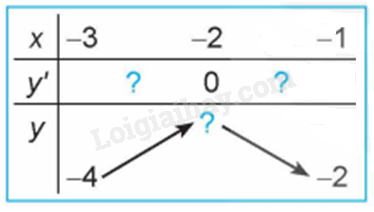
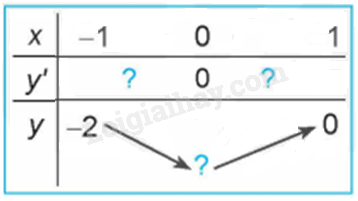
Bài 27 :
Xét sự đồng biến, nghịch biến của các hàm số sau:
a) \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\);
b) \(y = - {x^3} + 2{x^2} - 5x + 3\).
Bài 28 :
Tìm các khoảng đơn điệu của các hàm số sau:
a) \(y = \frac{{2x - 1}}{{x + 2}}\);
b) \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\).
Bài 29 :
Xét chiều biến thiên của các hàm số sau:
a) \(y = \sqrt {4 - {x^2}} \);
b) \(y = \frac{x}{{{x^2} + 1}}\).
Bài 30 :
Hàm số nào sau đây nghịch biến trên \(\mathbb{R}\)?
A. \(y = - {x^3} + 3{x^2} - 9x\);
B. \(y = - {x^3} + x + 1\);
C. \(y = \frac{{x - 1}}{{x - 2}}\);
D. \(y = 2{x^2} + 3x + 2\).












