Nội dung từ Loigiaihay.Com
Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M. Đường thẳng qua M vuông góc với AE cắt BC tại N. Chứng minh DM + BN = MN.
Chứng minh MD = MH, BN = HN ⇒ DM + BN = MH + HN = MN.
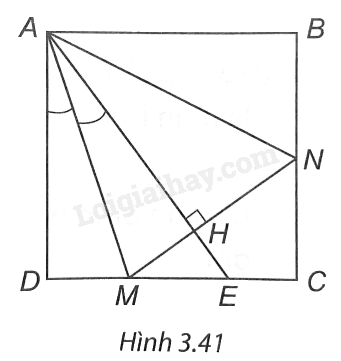
(H.3.41). Gọi H là giao điểm của AE với MN.
Xét hai tam giác vuông ADM và AHM có: AM là cạnh chung, \(\widehat {DAM} = \widehat {HAM}.\)
⇒ ∆ADM = ∆AHM (cạnh huyền – góc nhọn)
⇒ MD = MH và AD = AH.
Xét hai tam giác vuông AHN và ABN có:
AN là cạnh chung, AH = AB (vì cùng bằng AD).
⇒ ∆AHN = ∆ABN (cạnh huyền – cạnh góc vuông) ⇒ HN = BN.
Vậy DM + BN = MH + HN = MN.

Các bài tập cùng chuyên đề
Bài 1 :
Một hình vuông có chu vi là 32 cm. Hỏi diện tích hình vuông nhận giá trị nào sau đây?
-
A.
\(49c{m^2}\).
-
B.
\(64c{m^2}\).
-
C.
36\(c{m^2}\).
-
D.
81\(c{m^2}\).
Bài 2 :
Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M. Đường thẳng qua M vuông góc với AE cắt BC tại N.
Chứng minh DM + BN = MN.
Bài 3 :
Cho hình chữ nhật \(ABCD\). Giải thích tại sao \(ABCD\) là hình vuông trong mỗi trường hợp sau:
Trường hợp 1: \(AB = BC\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là đường phân giác của góc \(BAD\)
Bài 4 :
a) Mỗi hình vuông có là một hình chữ nhật hay không?
b) Mỗi hình vuông có là một hình thoi hay không?
Bài 5 :
Cho hình vuông ABCD. Tính số đo các góc CAB, DAC.
Bài 6 :
Từ tính chất của hình chữ nhật và hình thoi, em hãy nêu tính chất của đường chéo hình vuông.
Bài 7 :
Tính độ dài cạnh của hình vuông có đường chéo bằng \(5\,cm.\)
Bài 8 :
Cho hình vuông ABCD. Với điểm M nằm giữa C và D, kẻ tia phân giác của góc DAM; nó cắt CD ở N. Đường thẳng qua N vuông góc với AM cắt BC ở P. Tính số đo của góc NAP.
Bài 9 :
Cho hình vuông ABCD với tâm O và có cạnh bằng 2cm. Hai tia Ox, Oy tạo thành góc vuông. Tính diện tích của phần hình vuông nằm bên trong góc xOy.
Bài 10 :
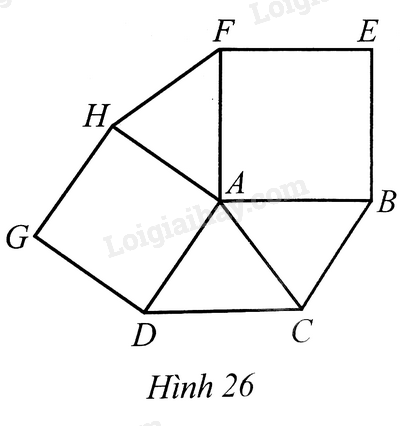
Cho hình bình hành \(ABCD\). Ở phía ngoài hình bình hành, vẽ các hình vuông \(ABEF\) và \(ADGH\) (Hình 26). Chứng minh:
a) \(\Delta AHF = \Delta ADC\)
b) \(AC \bot HF\).