Nội dung từ Loigiaihay.Com
Xác định vị trí tương đối của hai đường thẳng \({\Delta _1},{\Delta _2}\) trong mỗi trường hợp sau:
a) \({\Delta _1}:\frac{{x - 1}}{2} = \frac{{y - 2}}{1} = \frac{{z - 3}}{{ - 1}}\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 11 - 6t\\y = - 6 - 3t\\z = 10 + 3t\end{array} \right.\) (t là tham số);
b) \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 3t\\y = 2 + 4t\\z = 3 + 5t\end{array} \right.\) (t là tham số) và \({\Delta _2}:\frac{{x + 3}}{1} = \frac{{y + 6}}{2} = \frac{{z - 15}}{{ - 3}}\);
c) \({\Delta _1}:\frac{{x + 1}}{4} = \frac{{y - 1}}{3} = \frac{z}{1}\) và \({\Delta _2}:\frac{{x - 1}}{1} = \frac{{y - 3}}{2} = \frac{{z - 1}}{2}\).
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng để xét vị trí tương đối giữa hai đường thẳng: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng phân biệt \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({M_1},{M_2}\) và tương ứng có \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) là hai vectơ chỉ phương. Khi đó, ta có:
\({\Delta _1}//{\Delta _2} \Leftrightarrow \) \(\overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) cùng phương và \(\overrightarrow {{u_1}} ,\overrightarrow {{M_1}{M_2}} \) không cùng phương \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \overrightarrow 0 \\\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{M_1}{M_2}} } \right] \ne 0\end{array} \right.\).
\({\Delta _1}\) cắt \({\Delta _2}\) \( \Leftrightarrow \overrightarrow {{u_1}} \), \(\overrightarrow {{u_2}} \) không cùng phương và \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} ,\overrightarrow {{M_1}{M_2}} \) đồng phẳng \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} = 0\end{array} \right.\).
\({\Delta _1}\) và \({\Delta _2}\) chéo nhau \( \Leftrightarrow \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} \ne 0\).
a) Đường thẳng \({\Delta _1}\) có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {2;1; - 1} \right)\) và đi qua điểm \(A\left( {1;2;3} \right)\).
Đường thẳng \({\Delta _2}\) có vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( { - 6; - 3;3} \right)\) và đi qua điểm \(B\left( { - 11; - 6;10} \right)\).
Vì \( - 3\overrightarrow {{u_1}} = \left( { - 6; - 3;3} \right) = \overrightarrow {{u_2}} \), suy ra \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) cùng phương.
Lại có: \(\overrightarrow {AB} = \left( { - 12; - 8;7} \right)\) và \(\frac{2}{{ - 12}} \ne \frac{1}{{ - 8}}\) nên \(\overrightarrow {{u_1}} ,\overrightarrow {{M_1}{M_2}} \) không cùng phương.
Vậy \({\Delta _1}//{\Delta _2}\).
b) Đường thẳng \({\Delta _1}\) có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {3;4;5} \right)\) và đi qua điểm \(A\left( {1;2;3} \right)\).
Đường thẳng \({\Delta _2}\) có vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {1;2; - 3} \right)\) và đi qua điểm \(B\left( { - 3; - 6;15} \right)\).
Ta có: \(\frac{3}{1} \ne \frac{4}{2}\) nên \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) không cùng phương.
Lại có: \(\overrightarrow {AB} = \left( { - 4; - 8;12} \right)\), \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}4&5\\2&{ - 3}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}5&3\\{ - 3}&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}3&4\\1&2\end{array}} \right|} \right) = \left( { - 22;14;2} \right)\)
Vì \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {AB} = \left( { - 22} \right).\left( { - 4} \right) + 14.\left( { - 8} \right) + 2.12 = 0\) nên \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} ,\overrightarrow {AB} \) đồng phẳng. Vậy \({\Delta _1}\) cắt \({\Delta _2}\).
c) Đường thẳng \({\Delta _1}\) có vectơ chỉ phương \(\overrightarrow {{u_1}} = \left( {4;3;1} \right)\) và đi qua điểm \(A\left( { - 1;1;0} \right)\).
Đường thẳng \({\Delta _2}\) có vectơ chỉ phương \(\overrightarrow {{u_2}} = \left( {1;2;2} \right)\) và đi qua điểm \(B\left( {1;3;1} \right)\).
Ta có: \(\frac{4}{1} \ne \frac{3}{2}\) nên \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) không cùng phương.
Lại có: \(\overrightarrow {AB} = \left( {2;2;1} \right)\), \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}3&1\\2&2\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&4\\2&1\end{array}} \right|;\left| {\begin{array}{*{20}{c}}4&3\\1&2\end{array}} \right|} \right) = \left( {4; - 7;5} \right)\)
Vì \(\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {AB} = 4.2 - 7.2 + 5.1 = - 1 \ne 0\) nên \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} ,\overrightarrow {AB} \) không đồng phẳng. Vậy \({\Delta _1}\) và \({\Delta _2}\) chéo nhau.

Các bài tập cùng chuyên đề
Bài 1 :
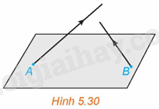
(H.5.30) Trong không gian Oxyz, có hai vật thể lần lượt xuất phát từ A(1; 2; 0) và B(3; 5; 0) với vận tốc không đổi tương ứng là \(\overrightarrow {{v_1}} = \left( {2;1;3} \right),\overrightarrow {{v_2}} = \left( {1;2;1} \right)\). Hỏi trong quá trình chuyển động, hai vật thể trên có va chạm vào nhau hay không?
Bài 2 :
Trong không gian Oxyz, xét vị trí tương đối giữa hai đường thẳng: \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + t\\z = 1 - t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = s\\y = 1 + 2s\\z = 3s\end{array} \right.\).
Bài 3 :
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1}:\frac{{x - 1}}{1} = \frac{{y + 2}}{1} = \frac{{z - 3}}{4}\) và \({\Delta _2}:\frac{{x + 1}}{1} = \frac{{y + 1}}{1} = \frac{z}{4}\). Chứng minh rằng:
a) Hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau;
b) Đường thẳng \({\Delta _1}\) và trục Ox chéo nhau;
c) Đường thẳng \({\Delta _2}\) trùng với đường thẳng \({\Delta _3}:\frac{{x + 2}}{1} = \frac{{y + 2}}{1} = \frac{{z + 4}}{4}\);
d) Đường thẳng \({\Delta _2}\) cắt trục Oz.
Bài 4 :
Trong không gian Oxyz, chứng minh rằng hai đường thẳng sau song song với nhau:
\({\Delta _1}:\frac{{x - 3}}{1} = \frac{y}{{ - 2}} = \frac{{z - 1}}{3}\) và \({\Delta _2}:\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{z}{3}\).
Bài 5 :
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 - t\\z = 2 + 3t\end{array} \right.\) và \({\Delta _2}:\frac{{x - 8}}{{ - 1}} = \frac{{y + 2}}{1} = \frac{{z - 2}}{2}\).
a) Chứng minh rằng \({\Delta _1}\) và \({\Delta _2}\) cắt nhau.
b) Viết phương trình mặt phẳng (P) chứa \({\Delta _1}\) và \({\Delta _2}\).
Bài 6 :
Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1}:\frac{{x - 1}}{3} = \frac{{y - 3}}{1} = \frac{{z - 2}}{2}\) và \({\Delta _2}:\frac{{x - 1}}{3} = \frac{{y + 1}}{1} = \frac{z}{2}\).
a) Chứng minh rằng \({\Delta _1}\) và \({\Delta _2}\) song song nhau.
b) Viết phương trình mặt phẳng (P) chứa \({\Delta _1}\) và \({\Delta _2}\).
Bài 7 :
Trong không gian Oxyz, xác định vị trí tương đối giữa hai đường thẳng: \({\Delta _1}:\left\{ \begin{array}{l}x = - 1 + t\\y = 1\\z = 3 + 2t\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 1 + 2s\\y = 2 + s\\z = 1 + 3s\end{array} \right.\).
Bài 8 :
Bằng cách giải hệ phương trình, xác định vị trí tương đối của hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = {t_1}\\y = 1\\z = 0\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 2\\y = {t_2}\\z = 0\end{array} \right.\).
Bài 9 :
Xác định vị trí tương đối của hai đường thẳng \({\Delta _1},{\Delta _2}\) trong mỗi trường hợp sau:
a) \({\Delta _1}:\frac{{x + 1}}{3} = \frac{{y + 5}}{4} = \frac{{z - 5}}{{ - 1}}\) và \({\Delta _2}:\frac{{x + 13}}{5} = \frac{{y - 5}}{{ - 2}} = \frac{{z + 17}}{7}\);
b) \({\Delta _1}:\frac{{x - 2}}{2} = \frac{{y + 1}}{3} = \frac{{z - 4}}{{ - 7}}\) và \({\Delta _2}:\frac{{x + 10}}{{ - 6}} = \frac{{y + 19}}{{ - 9}} = \frac{{z - 45}}{{21}}\);
c) \({\Delta _1}:\frac{{x + 3}}{1} = \frac{{y - 5}}{1} = \frac{{z - 2}}{3}\) và \({\Delta _2}:\frac{{x + 13}}{5} = \frac{{y - 9}}{{ - 2}} = \frac{{z + 13}}{7}\).
Bài 10 :
Cho ba đường thẳng \(d:\left\{ \begin{array}{l}x = 4 + t\\y = 1 + 2t\\z = 1 + 3t\end{array} \right.\), \(d':\left\{ \begin{array}{l}x = 2t'\\y = 7 + 4t'\\z = 2 + 6t'\end{array} \right.\); \(d'':\left\{ \begin{array}{l}x = 5 + 2t''\\y = 3 + 4t''\\z = 4 + 6t''\end{array} \right.\).
a) Nêu nhận xét về ba vectơ chỉ phương của \(d\), \(d'\) và \(d''.\)
b) Xét điểm \(M\left( {4;1;1} \right)\) nằm trên \(d\). Điểm \(M\) có nằm trên \(d'\) hoặc \(d''\) không?
c) Từ các kết quả trên, ta có thể kết luận gì về vị trí tương đối giữa \(d\) và \(d'\), \(d\) và \(d''\)?
Bài 11 :
Kiểm tra tính song song hoặc trùng nhau của các đường thẳng sau:
a) \(d:\left\{ \begin{array}{l}x = 7 + 4t\\y = 3 - 2t\\z = 2 - 2t\end{array} \right.\) và \(d':\frac{{x - 3}}{2} = \frac{{y - 5}}{{ - 1}} = \frac{{z - 4}}{{ - 1}}.\)
b) \(d:\frac{x}{3} = \frac{y}{3} = \frac{{z - 1}}{4}\) và \(d':\frac{{x - 2}}{3} = \frac{{y - 9}}{3} = \frac{{z - 5}}{4}.\)
Bài 12 :
Cho ba đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 3t\\z = 3 - t\end{array} \right.\); \(d':\left\{ \begin{array}{l}x = 2 - 2t'\\y = - 2 + t'\\z = 1 + 3t'\end{array} \right.\) và \(d'':\left\{ \begin{array}{l}x = 2 - 2t''\\y = - 2 + t''\\z = 3 + 3t''\end{array} \right.\)
a) Đường thẳng \(d'\) và đường thẳng \(d''\) có song song hay trùng với đường thẳng \(d\) không?
b) Giải hệ phương trình \(\left\{ \begin{array}{l}1 + t = 2 - 2t'\\2 + 3t = - 2 + t'\\3 - t = 1 + 3t'\end{array} \right.\) (ẩn \(t\) và \(t'\)).
Từ đó nhận xét về vị trí tương đối giữa \(d\) và \(d'.\)
c) Giải hệ phương trình \(\left\{ \begin{array}{l}1 + t = 2 - 2t''\\2 + 3t = - 2 + t''\\3 - t = 3 + 3t''\end{array} \right.\) (ẩn \(t\) và \(t''\)).
Từ đó nhận xét về vị trí tương đối giữa \(d\) và \(d''.\)
Bài 13 :
Xét vị trí tương đối giữa hai đường thẳng \(d\) và \(d'\) trong mỗi trường hợp sau:
a) \(d:\left\{ \begin{array}{l}x = 2t\\y = 1 - t\\z = 2 - 3t\end{array} \right.\) và \(d':\frac{{x - 2}}{4} = \frac{y}{7} = \frac{{z + 1}}{{11}}.\)
b) \(d:\frac{{x - 4}}{1} = \frac{{y - 1}}{2} = \frac{{z - 1}}{2}\) và \(d':\frac{{x - 2}}{3} = \frac{{y - 1}}{2} = \frac{{z - 1}}{9}.\)
Bài 14 :
Trên phần mềm thiết kế chiếc cầu treo, cho đường thẳng \(d\) trên trụ cầu và đường thẳng \(d'\) trên sàn cầu có phương trình lần lượt là: \(d:\left\{ \begin{array}{l}x = 0\\y = 0\\z = 50 + t\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 20\\y = t'\\z = 50\end{array} \right.\).
Xét vị trí tương đối giữa \(d\) và \(d'.\)

Bài 15 :
Cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 4 + t\\y = 1 + 2t\\z = 1 - t\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = t'\\y = 7 + 4t'\\z = 9t'\end{array} \right.\).
a) Tìm vectơ chỉ phương \(\vec a\) và \(\vec a'\) lần lượt của \(d\) và \(d'.\)
b) Tính tích vô hướng \(\vec a.\vec a'\). Từ đó, có nhận xét gì về hai đường thẳng \(d\) và \(d'?\)
Bài 16 :
Kiểm tra tính vuông góc của các cặp đường thẳng sau:
a) \(d:\frac{x}{1} = \frac{{y + 1}}{{ - 3}} = \frac{z}{1}\) và \(d':\left\{ \begin{array}{l}x = - 2 + t\\y = t\\z = - 6 + 2t\end{array} \right.\).
b) \(d:\frac{{x + 2}}{7} = \frac{{y + 1}}{3} = \frac{{z + 1}}{1}\) và \(d':\frac{{x + 2}}{2} = \frac{{y - 5}}{2} = \frac{{z - 5}}{2}.\)
Bài 17 :
Một phần mềm mô phỏng vận động viên đang tập bắn sứng trong không gian \(Oxyz\). Cho biết trục \(d\) của nòng súng và cọc đỡ bia \(d'\) có phương trình lần lượt là \(d:\left\{ \begin{array}{l}x = t\\y = 20\\z = 9\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 10\\y = 20\\z = 1 + 3t'\end{array} \right.\). Xét vị trí tương đối giữa \(d\) và \(d'\), chúng có vuông góc với nhau không?
Bài 18 :
Xét vị trí tương đối giữa các cặp đường thẳng sau:
a) \(d:\left\{ \begin{array}{l}x = 1 + t\\y = - 1 + 2t\\z = - 2 + t\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 2 + 2t'\\y = 3 + 4t'\\z = 2t'\end{array} \right.\)
b) \(d:\frac{{x - 1}}{1} = \frac{{y - 2}}{2} = \frac{{z - 3}}{2}\) và \(d':\frac{{x - 2}}{1} = \frac{{y - 1}}{5} = \frac{{z - 1}}{1}\).
Bài 19 :
Trên phần mềm mô phỏng 3D một máy khoan trong không gian \(Oxyz\), cho biết phương trình trục \(a\) của mũi khoan và một đường rãnh \(b\) trên vật cần khoan (hình dưới đây) lần lượt là \(a:\left\{ \begin{array}{l}x = 1\\y = 2\\z = 3t\end{array} \right.\) và \(b:\left\{ \begin{array}{l}x = 1 + 4t'\\y = 2 + 2t'\\z = 6\end{array} \right.\).
a) Chứng minh \(a\), \(b\) vuông góc và cắt nhau.
b) Tìm toạ độ giao điểm của \(a\) và \(b\).
Bài 20 :
Cho đường thẳng \(d:\left\{ \begin{array}{l}x = - 1 + 2t\\y = - t\\z = - 2 - t\end{array} \right.\). Trong các đường thẳng sau, đường thẳng nào vuông góc với \(d\)?
A. \({d_1}:\left\{ \begin{array}{l}x = 3t'\\y = 1 + t'\\z = 5t'\end{array} \right.\)
B. \({d_2}:\left\{ \begin{array}{l}x = 2\\y = 2 + t'\\z = 1 + t'\end{array} \right.\)
C. \({d_3}:\frac{{x - 2}}{3} = \frac{y}{2} = \frac{{z - 1}}{{ - 5}}\)
D. \({d_4}:\frac{{x + 2}}{2} = \frac{y}{{ - 1}} = \frac{{z + 1}}{2}\)
Bài 21 :
Xác định vị trí tương đối của hai đường thẳng \({\Delta _1},{\Delta _2}\) trong mỗi trường hợp sau:
a) \({\Delta _1}:\frac{{x + 7}}{5} = \frac{{y - 1}}{{ - 7}} = \frac{{z + 2}}{{ - 2}}\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 5 - 3t\\y = - 10 - 4t\\z = 3 + 7t\end{array} \right.\) (với \(t\) là tham số);
b) \({\Delta _1}:\left\{ \begin{array}{l}x = - 2 + 5t\\y = 1 - t\\z = 3t\end{array} \right.\) (với \(t\) là tham số) và \({\Delta _2}:\frac{{x + 2}}{4} = \frac{{y - 1}}{5} = \frac{{z - 1}}{{ - 6}}\);
c) \({\Delta _1}:\frac{x}{3} = \frac{{y + 5}}{2} = \frac{{z - 1}}{{ - 3}}\) và \({\Delta _2}:\frac{{x - 1}}{{ - 6}} = \frac{{y - 3}}{{ - 4}} = \frac{{z - 1}}{6}\).
Bài 22 :
Cho hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 11 - 3{t_1}\\y = - 5 + 4{t_1}\\z = m{t_1}\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 4 + 5{t_2}\\y = 2 + 3{t_2}\\z = 2{t_2}\end{array} \right.\), với \(m\) là tham số thực; \({t_1},{t_2}\) là tham số của phương trình đường thẳng. Tìm \(m\) để hai đường thẳng đó vuông góc với nhau.
Bài 23 :
Xác định vị trí tương đối của hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) trong mỗi trường hợp sau:
a) \({\Delta _1}:\frac{{x + 2}}{9} = \frac{{y - 1}}{{27}} = \frac{{z - 3}}{{ - 27}}\) và \({\Delta _2}:\frac{{x + 1}}{{ - 1}} = \frac{{y - 3}}{{ - 3}} = \frac{{z - 7}}{3}\);
b) \({\Delta _1}:\frac{{x + 1}}{{ - 2}} = \frac{{y - 6}}{5} = \frac{{z + 3}}{{ - 4}}\) và \({\Delta _2}:\frac{{x + 13}}{7} = \frac{{y + 9}}{5} = \frac{{z + 15}}{8}\);
c) \({\Delta _1}:\frac{{x + 3}}{2} = \frac{{y + 6}}{3} = \frac{{z + 3}}{2}\) và \({\Delta _2}:\frac{{x + 17}}{2} = \frac{{y - 33}}{{ - 3}} = \frac{{z + 16}}{2}\).
Bài 24 :
Cho hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 4{t_1}\\y = 9 + {t_1}\\z = 1 - 6{t_1}\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 4 + 3{t_2}\\y = 1 - 18{t_2}\\z = - 5 - {t_2}\end{array} \right.\) (\({t_1},{t_2}\) là tham số). Chứng minh rằng \({\Delta _1} \bot {\Delta _2}\).
Bài 25 :
Trong không gian Oxyz, cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 1 - 1t\\y = 2 + t\\z = - 3 + 2t\end{array} \right.\) và \(d':\frac{{x + 2}}{3} = \frac{{y + 1}}{2} = \frac{z}{{ - 1}}\).
Xét vị trí tương đối giữa \(d\) và \(d'\).
Bài 26 :
Trong không gian Oxyz, cho hai đường thẳng:
\(\Delta :\left\{ \begin{array}{l}x = 1 - t\\y = 2 + t\\z = - 1 + 2t\end{array} \right.\) và \(\Delta ':\frac{{x - 2}}{2} = \frac{{y - 1}}{1} = \frac{{z + 3}}{{ - 3}}\).
Vị trí tương đối của hai đường thẳng này là
A. chéo nhau.
B. cắt nhau.
C. song song.
D. trùng nhau.
Bài 27 :
Xác định vị trí tương đối của hai đường thẳng \(d\) và \(d'\) trong mỗi trường hợp sau:
a) \(d:\left\{ \begin{array}{l}x = t\\y = 1 + 3t\\z = 1 - t\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 2 + 2t'\\y = 7 + 6t'\\z = - 1 - 2t'\end{array} \right.\);
b) \(d:\frac{{x - 2}}{2} = \frac{y}{3} = \frac{z}{1}\) và \(d':\frac{x}{4} = \frac{y}{6} = \frac{z}{2}\);
c) \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 1 + t\\z = 2 - t\end{array} \right.\) và \(d':\frac{{x - 2}}{2} = \frac{{y - 2}}{3} = \frac{{z - 1}}{1}\).
b) \(d:\frac{{x - 1}}{2} = \frac{{y - 1}}{1} = \frac{{z - 2}}{1}\) và \(d':\left\{ \begin{array}{l}x = 2\\y = 1 + t\\z = 7\end{array} \right.\);
Bài 28 :
Trong không gian Oxyz cho trước (1 đơn vị = 1 cm), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử tại thời điểm \(t\) (tính bằng phút), kiến vàng ở vị trí \((6 + t;8 - t;3 + t)\) trên đường thẳng \({d_1}\). Cùng thời điểm đó, kiến đen ở vị trí
\((1 + t;2 + t;2t)\) trên đường thẳng \({d_2}\).
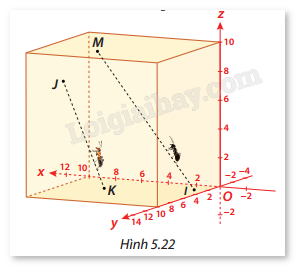
a) Chứng minh rằng hai chú kiến bò trên hai đường thẳng chéo nhau.
b) Tính khoảng cách giữa hai chú kiến tại các thời điểm \(t = 0\) và \(t = 10\).
c) Hỏi tại thời điểm nào thì khoảng cách giữa hai chú kiến là nhỏ nhất? Tính khoảng cách đó.
Bài 29 :
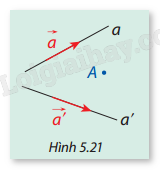
Trong không gian, cho hai đường thẳng a và a' lần lượt là giá của hai vectơ (khác \(\overrightarrow 0 \)) \(\vec a\) và \(\vec a'\) (Hình 5.21). Từ một điểm A bất kỳ, vẽ hai đường thẳng d và d' lần lượt song song với a và a'.
a) Hỏi a và a' có phải lần lượt là vectơ chỉ phương của d và d' không? Vì sao?
b) Nếu \(d \bot d'\), thì \(\vec a\) và \(\vec a'\) có vuông góc nhau không? Vì sao?
Bài 30 :
Trong không gian Oxyz, xét vị trí tương đối của các cặp đường thẳng sau:
a) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = 4 + t}\\{z = 5 - 2t}\end{array}} \right.\quad (t \in \mathbb{R})\) và \(d':\left\{ {\begin{array}{*{20}{l}}{x = 2 - 3t'}\\{y = 5 + 3t'}\\{z = 3 - 6t'}\end{array}} \right.\quad (t' \in \mathbb{R}){\rm{ }}\)
b) \(d:\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z - 3}}{{ - 1}}\) và \(d':\frac{{x - 2}}{{ - 2}} = \frac{{y + 2}}{1} = \frac{{z - 1}}{3}\)
c) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 2 + t}\\{z = - 3 + 3t}\end{array}} \right.\quad (t \in \mathbb{R}){\rm{ }}\) và \(d':\frac{{x - 2}}{1} = \frac{{y + 3}}{2} = \frac{{z - 1}}{3}{\rm{ }}\)












