Nội dung từ Loigiaihay.Com
a) Nguyên liệu của món mứt dừa sau khi hoàn thành chỉ gồm dừa và đường theo tỷ lệ 2 : 1. Tính xem trong 6 kg mứt dừa có bao nhiêu ki-lô-gam dừa và bao nhiêu ki-lô-gam đường.
b) Bạn Dũng và bạn Thủy muốn làm mứt gừng theo công thức: Cứ 3 phần gừng thì cần 2 phần đường. Hai bạn mua 600g gừng. Hai bạn cần mua bao nhiêu gam đường?
c) Mẹ chỉ có 10 quyển vở, số vở chia cho hai chị em An và Bình. Tính số sách chia cho mỗi em, biết rằng số tuổi của An và Bình là 8; 12 và số sách tỉ lệ thuận với số tuổi
a) Theo tỉ lệ 2:1 thì trong 6kg mứt dừa sẽ có 3 phần nguyên liệu bằng nhau trong đó 2 phần là dừa còn lại là đường .
b) Từ số phần gừng và đường ta suy ra được tỉ lệ của gừng và đường . Sau đó lấy tỉ lệ nhân với số gừng đã mua để ra só đường cần mua .
c) Tính tỉ lệ quyển vở của 2 chị em và vì An nhỏ tuổi hơn nên tỉ lệ của An thấp hơn. Sau đó rút gọn tỉ lệ để tìm được số vở của mỗi người dựa vào số vở đã cho có ở đầu bài.
a) Tỉ lệ dừa và đường là : \(\dfrac{2}{1}\)
Ta có sơ đồ sau :
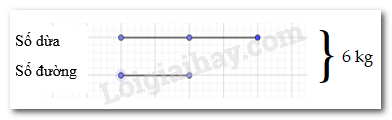
\( \Rightarrow \) Số kg đường là : 6 : ( 2+1) = 2 (kg) ( Áp dụng bài toán tổng tỉ đã học ở tiểu học )
\( \Rightarrow \) Số kg dừa là : 2 . 2 = 4 (kg)
b) Tỉ lệ của gừng và đường là 3:2 ta có được tỉ số giữa gừng và đường là \(\dfrac{3}{2}\) nên số đường bằng \(\dfrac{2}{3}\) số gừng.
Theo đề bài hai bạn đã mua 600 g gừng nên
\( \Rightarrow \) Số đường cần mua là : \(\dfrac{2}{3} \times 600\)= 400 g
Vậy 2 bạn cần mua 400g đường
c) Ta có số tuổi của An và Bình lần lượt là 8;12 nên ta sẽ có tỉ số tuổi của 2 bạn là \(\dfrac{8}{{12}} = \dfrac{2}{3}\)
Vậy số sách của An và Bình sẽ có tỉ số là 2:3
Theo đề bài chị Chi có 10 quyển vở mà theo tỉ số vừa tính được trong số 10 quyển vở đó An có 2 phần và Bình có 3 phần .
\( \Rightarrow \) Số vở của An là 10 : ( 2+3) . 2 = 4 quyển vở ( Áp dụng bài toán tổng tỉ đã được học ở lớp dưới )
\( \Rightarrow \) Số vở của Bình là : 10 – 4 = 6 quyển vở .

Các bài tập cùng chuyên đề
Bài 1 :
Cho \(7x = 4y\) và \(y - x = 24\). Tính \(x;y\).
-
A.
\(y = 4;x = 7\)
-
B.
\(x = 32;y = 56\)
-
C.
\(x = 56;y = 32\)
-
D.
\(x = 4;y = 7\)
Bài 2 :
Cho \(\dfrac{x}{2} = \dfrac{y}{5}\) và \(xy = 10\). Tính \(x - y\) biết \(x > 0;y > 0.\)
-
A.
\( - 3\)
-
B.
\(3\)
-
C.
\(8\)
-
D.
\( - 8\)
Bài 3 :
Học sinh của ba lớp 7A, 7B, 7C làm 40 tấm thiệp để chúc mừng các thầy cô nhân ngày 20-11, biết số học sinh của ba lớp 7A, 7B, 7C theo thứ tự là 45; 42; 33. Hỏi trong ba lớp trên mỗi lớp làm bao nhiêu tấm thiệp, biết số học sinh tỉ lệ với số thiệp cần làm.
Bài 4 :
Làm thế nào để biểu diễn sự bằng nhau của ba tỉ số \(\frac{1}{2};\frac{2}{4};\frac{3}{6}\)?
Bài 5 :
Viết dãy tỉ số bằng nhau từ các tỉ số:
\(\frac{1}{4};\frac{8}{{32}};\frac{{13}}{{54}};\frac{{ - 9}}{{ - 36}}\)
Bài 6 :
a) Cho tỉ lệ thức\(\frac{6}{{10}} = \frac{9}{{15}}\). So sánh hai tỉ số \(\frac{{6 + 9}}{{10 + 15}}\) và \(\frac{{6 - 9}}{{10 - 15}}\) với các tỉ số trong tỉ lệ thức đã cho.
b) Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\) với \(b + d \ne 0;b - d \ne 0\)
Gọi giá trị trung của các tỉ số đó là k, tức là: \(k = \frac{a}{b} = \frac{c}{d}\)
- Tính a theo b và k, tính c theo d và k.
- Tính tỉ số \(\frac{{a + c}}{{b + d}}\) và \(\frac{{a - c}}{{b - d}}\) theo k.
- So sánh mỗi tỉ số \(\frac{{a + c}}{{b + d}}\) và \(\frac{{a - c}}{{b - d}}\) với các tỉ số \(\frac{a}{b}\) và \(\frac{c}{d}\)
Bài 7 :
Tìm hai số x,y biết:
x : 1,2 = y : 0,4 và x – y = 2.
Bài 8 :
Tìm ba số x,y,z biết x,y,z tỉ lệ với ba số 2,3,4 và x – y – z = 2.
Bài 9 :
Ba máy bơm cùng bơm nước vào một bể bơi không có nước, có dạng hình hộp chữ nhật, với các kích thước bể là 12 m; 10 m; 1,2 m. Lượng nước mà ba máy bơm được tỉ lệ với 3 số 7;8;9. Mỗi máy cần bơm bao nhiêu mét khối nước để đầy bể bơi?
Bài 10 :
Cho tỉ lệ thức \(\frac{x}{7} = \frac{y}{2}\). Tìm hai số x,y biết:
a) x + y = 18;
b) x – y = 20
Bài 11 :
Cho dãy tỉ số bằng nhau \(\frac{x}{3} = \frac{y}{4} = \frac{z}{5}\). Tìm ba số x,y,z biết:
a) x+y+z = 180; b) x + y – z = 8
Bài 12 :
Cho ba số x,y,z sao cho \(\frac{x}{3} = \frac{y}{4};\frac{y}{5} = \frac{z}{6}\)
a) Chứng minh: \(\frac{x}{{15}} = \frac{y}{{20}} = \frac{z}{{24}}\)
b) Tìm ba số x,y,z biết x – y + z = - 76
Bài 13 :
Cho \(\frac{a}{b} = \frac{c}{d}\) với b – d \( \ne \) 0; b + 2d \( \ne \) 0. Chứng tỏ rằng:
\(\frac{{a - c}}{{b - d}} = \frac{{a + 2c}}{{b + 2d}}\)
Bài 14 :
Tìm ba số x,y,z biết: \(\frac{x}{5} = \frac{y}{7} = \frac{z}{9}\) và x – y + z = \(\frac{7}{3}\)
Bài 15 :
Ba lớp 7A, 7B và 7C được giao nhiệm vụ trồng 120 cây để phủ xanh đổi trọc. Tính số cây trồng được của mỗi lớp, biết số cây trồng được của ba lớp 7A, 7B và 7C tỉ lệ với 7; 8; 9.
-
A.
Số cây lớp 7A, 7B, 7C trồng được lần lượt là 35 cây; 40 cây; 42 cây;
-
B.
Số cây lớp 7A, 7B, 7C trồng được lần lượt là 35 cây; 38 cây; 42 cây;
-
C.
Số cây lớp 7A, 7B, 7C trồng được lần lượt là 35 cây; 40 cây; 38 cây;
-
D.
Số cây lớp 7A, 7B, 7C trồng được lần lượt là 35 cây; 40 cây; 45 cây;
Bài 16 :
Tìm hai số x, y biết:
a) \(\dfrac{x}{3} = \dfrac{y}{4}\) và \(x + y = 14\);
b) \(\dfrac{x}{4} = \dfrac{y}{{ - 7}}\) và \(x - y = 33\);
c) \(x:y = 2\dfrac{2}{3}\) và \(x - y = 60\);
d) \(x:3 = y:16\) và \(3x - y = 35\).
Bài 17 :
Tìm ba số x, y, z biết:
a) \(\dfrac{x}{3} = \dfrac{y}{5} = \dfrac{z}{6}\) và \(x + y + z = 98\);
b) \(\dfrac{x}{5} = \dfrac{y}{{ - 6}} = \dfrac{z}{7}\) và \(x - y - z = 16\);
c) \(x:y:z = 2:3:4\) và \(x + 2y - z = - 8\);
d) \(\dfrac{x}{{ - 3}} = \dfrac{y}{4};{\rm{ }}\dfrac{y}{2} = \dfrac{z}{3}\) và \(x + y + z = 14\).
Bài 18 :
Cho tỉ lệ thức \(\dfrac{a}{b} = \dfrac{c}{d}\), hãy chứng tỏ mỗi tỉ lệ thức sau:
a) \(\dfrac{{a + b}}{b} = \dfrac{{c + d}}{d}\);
b) \(\dfrac{{a - b}}{b} = \dfrac{{c - d}}{d}\).
Bài 19 :
Tìm ba số x, y, z biết:
a) \(2x = 3y;{\rm{ }}5y = 7z\) và \(3x - 7y + 5z = 30\);
b) \(\dfrac{{x - 1}}{2} = \dfrac{{y - 2}}{3} = \dfrac{{z - 3}}{4}\) và \(x - 2y + 3z = 14\).
Bài 20 :
Cho các số a, b, c thỏa mãn \(\dfrac{a}{{2{\rm{ }}020}} = \dfrac{b}{{2{\rm{ }}021}} = \dfrac{c}{{2{\rm{ }}022}}\). Chứng tỏ rằng:
\(4(a - b)(b - c) = {(c - a)^2}\).
Bài 21 :
Tìm hai số x và y biết: \(\dfrac{x}{{11}} = \dfrac{y}{{17}}\) và x – y = 12
Bài 22 :
Tìm hai số x và y, biết: \(\dfrac{x}{9} = \dfrac{y}{{11}}\) và x+y = 40
Bài 23 :
Tìm hai số x và y, biết: \(\dfrac{x}{{17}} = \dfrac{y}{{21}}\) và x - y= 8
Bài 24 :
Tìm x và y, biết: a) \(\dfrac{x}{y} = \dfrac{5}{3}\) và x+y = 16; b) \(\dfrac{x}{y} = \dfrac{9}{4}\) và x – y = -15
Bài 25 :
Tìm ba số x,y,z biết rằng: \(\dfrac{x}{2} = \dfrac{y}{3} = \dfrac{z}{4}\) và x+2y – 3z = -12
Bài 26 :
Cho tỉ lệ thức \(\dfrac{3}{7} = \dfrac{9}{{21}}\). Hãy tính các tỉ số \(\dfrac{{3 + 9}}{{7 + 21}}\) và \(\dfrac{{3 - 9}}{{7 - 21}}\) rồi so sánh chúng với các tỉ số trong tỉ lệ thức đã cho.
Bài 27 :
Tìm hai số x, y biết rằng:
a) x + y = 30 và \(\dfrac{x}{2}\)= \(\dfrac{y}{3}\)
b) x – y = −21 và \(\dfrac{x}{5}\)= \(\dfrac{y}{{ - 2}}\)
Bài 28 :
Tìm ba số x, y, z, biết x + y + z = 100 và x : y : z = 2 : 3 : 5
Bài 29 :
Tìm hai số x,y biết rằng:
a) \(\dfrac{x}{4} = \dfrac{y}{7}\) và x + y = 55
b) \(\dfrac{x}{8} = \dfrac{y}{3}\) và x – y = 35
Bài 30 :
a) Tìm hai số a,b biết rằng 2a = 5b và 3a + 4b = 46
b) Tìm hai số a,b,c biết rằng a : b : c = 2 : 4 : 5 và a + b – c = 3












