Cho đa thức P thỏa mãn \(\left( {x - 1} \right)P = {x^3} - 1\). Khi đó đa thức P là

Bài 1 :

Với hai số \(a,b\) bất kì, viết \(a - b = a + \left( { - b} \right)\) và áp dụng hằng đẳng thức lập phương của một tổng để tính \({a^3} + \left( { - {b^3}} \right)\).

Từ đó rút ra liên hệ giữa \({a^3} - {b^3}\) và \(\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\).

Bài 2 :

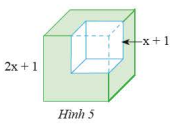
Từ một khối lập phương có cạnh bằng \(2x + 1\), ta cắt bỏ một khối lập phương có cạnh bằng \(x + 1\) (xem Hình 5). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.

Bài 3 :

Cho \(a\) và \(b\) là hai số thực bất kì.

a) Thực hiện phép tính \(\left( {a - b} \right)\left( {{a^2} + ab + {b^2}} \right)\)

b) \({a^3} - {b^3} = ?\)

Bài 4 :

a) Tính \(\left( {a - 4} \right)\left( {{a^2} + 4a + 16} \right).\)

b) Viết \(64{x^3} - 27{y^3}\) dưới dạng tích.

Bài 5 :

Đa thức \({x^3} - 8\) được phân tích thành tích của hai đa thức

A.\(x - 2\) và \({x^2} - 2x - 4\) 

B. \(x - 2\) và \({x^2} + 2x - 4\)

C. \(x - 2\) và \({x^2} + 2x + 4\)        

D. \(x - 2\) và \({x^2} - 2x + 4\)

Bài 6 :

Đa thức \(8{x^3} - 27{y^3}\) được viết thành tích của hai đa thức:

A. \(2x + 3y\) và \(4{x^2} - 6xy + 9{y^2}\).

B. \(2x + 3y\) và \(4{x^2} + 6xy + 9{y^2}\).

C. \(2x-3y\) và \(4{x^2} - 6xy + 9{y^2}\).

D. \(2x-3y\) và \(4{x^2} + 6xy + 9{y^2}\).

Bài 7 :

Vế phải của hằng đẳng thức: \(x^3−y^3=....\) là:

Bài 8 :

Bài 9 :

Biểu thức \(\left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right)\) là dạng phân tích đa thức thành nhân tử của đa thức

Bài 10 :

Cho đa thức P thỏa mãn \(\left( {x - 1} \right).P = {x^3} - 1\). Khi đó đa thức P là: