Nội dung từ Loigiaihay.Com
Ở Hình 6 có \(\hat A = \hat B = 60^\circ \) và Cx là tia phân giác của góc ACy. Chứng minh Cx song song với AB.
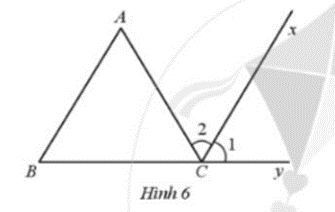
Chứng minh: \(\widehat {B{}_1} = \widehat {{C_1}}\) suy ra Cx // AB (vì hai góc đồng vị bằng nhau)
Vì \(\widehat {ACy}\) là góc ngoài của ∆ABC tại đỉnh C nên \(\widehat {ACy} = \hat A + \hat B\).
Do đó \(\widehat {ACy} = 60^\circ + 60^\circ = 120^\circ \)
Vì Cx là tia phân giác của góc ACy nên \({\hat C_1} = {\hat C_2} = \frac{{\widehat {ACy}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \)
Suy ra \(\hat B = {\hat C_1}\) (cùng bằng 60°), mà chúng ở vị trí đồng vị nên Cx // AB.
Vậy Cx // AB.

Các bài tập cùng chuyên đề
Bài 1 :
Cho hình sau. Tính số đo x:
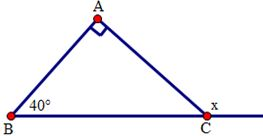
-
A.
\({90^0}\)
-
B.
\({100^0}\)
-
C.
\({120^0}\)
-
D.
\({130^0}\)
Bài 2 :
Góc ngoài của tam giác là:
-
A.
góc kề bù với một góc trong của tam giác
-
B.
góc phụ nhau với một góc trong của tam giác
-
C.
bằng hiệu của hai góc trong không kề với nó
-
D.
bằng góc kề với nó
Bài 3 :
Tìm các số đo góc x, y trong Hình 4.5.
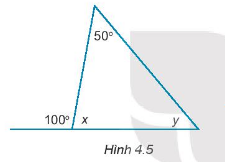
Bài 4 :
Tìm số đo các góc B và C của tam giác ABC trong Hình 4.6.
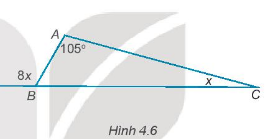
Bài 5 :
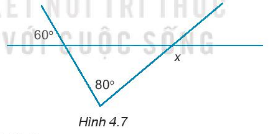
Tìm số đo góc x trong Hình 4.7.
Bài 6 :
Quan sát hình 3:
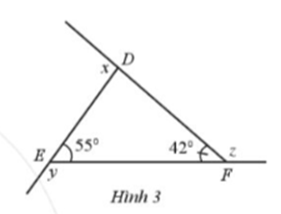
a) Tính số đo góc x, y, z.
b) Hãy nhận xét về tổng các số đo góc x + y + z












