Nội dung từ Loigiaihay.Com
Cho tam giác $ABC$ đều nội tiếp đường tròn $\left( O \right)$. Tính số đo cung $AC$ lớn.
-
A.
$240^\circ $
-
B.
$120^\circ $
-
C.
$360^\circ $
-
D.
$210^\circ $
Sử dụng định lý tổng các góc trong tam giác và số đo cung.
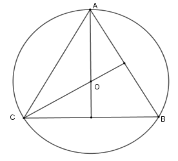
Vì tam giác $ABC$ đều có $O$ là tâm đường tròn ngoại tiếp nên $O$ cũng là giao ba đường phân giác nên $AO;CO$ lần lượt là các đường phân giác $\widehat {BAC}$; $\widehat {ACB}$.
Ta có $\widehat {CAO} = \dfrac{1}{2}\widehat {BAC} = \dfrac{{60^\circ }}{2} = 30^\circ $;$\widehat {ACO} = \dfrac{1}{2}\widehat {ACB} = \dfrac{{60^\circ }}{2} = 30^\circ $
Xét tam giác $AOC$ có $\widehat {AOC} = 180^\circ - \widehat {CAO} - \widehat {ACO} = 120^\circ $ nên số đo cung nhỏ $AC$ là $120^\circ $.
Do đó số đo cung lớn $AC$ là $360^\circ - 120^\circ = 240^\circ $.
Đáp án : A

Các bài tập cùng chuyên đề
Chọn khẳng định đúng. Góc ở tâm là góc
Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng
Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn
Cho đường tròn \(\left( {O;R} \right).\) Gọi \(H\) là trung điểm của bán kính \(OA\). Dây \(CD\) vuông góc với \(OA\) tại $H$ . Tính số đo cung lớn \(CD.\)
Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) vẽ góc ở tâm \(\widehat {AOC} = 55^\circ \) . Vẽ dây \(CD\) vuông góc với \(AB\) và dây \(DE\) song song với \(AB.\) Tính số đo cung nhỏ \(BE\)












