Nội dung từ Loigiaihay.Com
Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) vẽ góc ở tâm \(\widehat {AOC} = 55^\circ \) . Vẽ dây \(CD\) vuông góc với \(AB\) và dây \(DE\) song song với \(AB.\) Tính số đo cung nhỏ \(BE\)
-
A.
$55^\circ $
-
B.
$60^\circ $
-
C.
$40^\circ $
-
D.
$50^\circ $
Bước 1: Chứng minh $E;O;C$ thẳng hàng
Bước 2: Tính số đo cung thông qua góc ở tâm
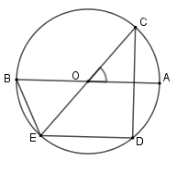
Xét $\left( O \right)$ có $CD \bot OA;ED{\rm{//}}OA \Rightarrow CD \bot ED$ hay $\widehat {EDC} = 90^\circ $ mà $E;D;C \in \left( O \right)$ nên $EC$ là đường kính của $\left( O \right)$ hay $E;O;C$ thẳng hàng.
Do đó $\widehat {BOE} = \widehat {COA} = 55^\circ $ (đối đỉnh) nên số đo cung nhỏ $BE$ là $55^\circ $.
Đáp án : A

Các bài tập cùng chuyên đề
Chọn khẳng định đúng. Góc ở tâm là góc
Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng
Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn
Cho tam giác $ABC$ đều nội tiếp đường tròn $\left( O \right)$. Tính số đo cung $AC$ lớn.
Cho đường tròn \(\left( {O;R} \right).\) Gọi \(H\) là trung điểm của bán kính \(OA\). Dây \(CD\) vuông góc với \(OA\) tại $H$ . Tính số đo cung lớn \(CD.\)












