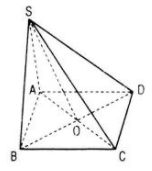
Câu 2 trang 91 SGK Hình học 11 Nâng cao

Đề bài

Cho hình chóp S.ABCD.

a. Chứng minh rằng nếu ABCD là hình bình hành thì $\overrightarrow {SB}  + \overrightarrow {SD}  = \overrightarrow {SA}  + \overrightarrow {SC}$. Điều ngược lại có đúng không ?

b. Gọi O là giao điểm của AC và BD. Chứng tỏ rằng ABCD là hình bình hành khi và chỉ khi $\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  + \overrightarrow {SD}  = 4\overrightarrow {SO}$

Lời giải chi tiết

a. Ta có:

$\eqalign{  & \overrightarrow {SB}  + \overrightarrow {SD}  = \overrightarrow {SA}  + \overrightarrow {SC}   \cr  &  \Leftrightarrow \overrightarrow {SB}  - \overrightarrow {SC}  = \overrightarrow {SA}  - \overrightarrow {SD}  \cr&\Leftrightarrow \overrightarrow {CB}  = \overrightarrow {DA}  \cr}$

⇔ ABCD là hình bình hành.

b. Ta có:

$\eqalign{  & \overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  + \overrightarrow {SD}  = 4\overrightarrow {SO}   \cr  &  \Leftrightarrow \overrightarrow {SO}  + \overrightarrow {OA}  + \overrightarrow {SO}  + \overrightarrow {OB} \cr& + \overrightarrow {SO}  + \overrightarrow {OC}  + \overrightarrow {SO}  + \overrightarrow {OD}  = 4\overrightarrow {SO}   \cr  &  \Leftrightarrow \overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \overrightarrow 0 \,\,\left( * \right) \cr}$

Nếu ABCD là hình bình hành thì $\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  = \overrightarrow 0$ suy ra

 $\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  + \overrightarrow {SD}  = 4\overrightarrow {SO}$ (do (*))

Ngược lại, giả sử $\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  + \overrightarrow {SD}  = 4\overrightarrow {SO} ,$ ta có (*).

Gọi M, N lần lượt là trung điểm của AC, BD thì :

$\overrightarrow {OA}  + \overrightarrow {OC}  = 2\overrightarrow {OM} ,\overrightarrow {OB}  + \overrightarrow {OD}  = 2\overrightarrow {ON}$

Từ (*) suy ra $2\left( {\overrightarrow {OM}  + \overrightarrow {ON} } \right) = \overrightarrow 0 ,$ điều này chứng tỏ O, M, N thẳng hàng

Mặt khác, M thuộc AC, N thuộc BD và O là giao điểm của AC và BD nên O, M, N thẳng hàng chỉ xảy ra khi O ≡ M ≡ N, tức O là trung điểm AC và BD, hay ABCD là hình bình hành.

HocTot.XYZ