Bài 2 trang 98 SGK Hình học 10

LG a

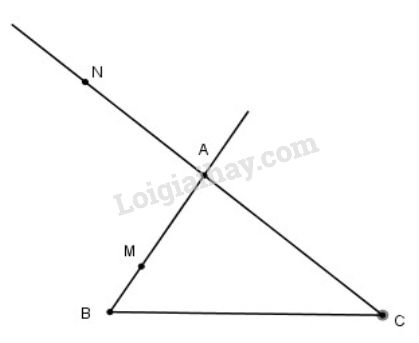
Hãy vẽ \(\displaystyle M, N\) khi \(\displaystyle \alpha  = {2 \over 3};\beta  =  - {2 \over 3}\)

Lời giải chi tiết:

Ta có:

\(\eqalign{
& \overrightarrow {AM} = {2 \over 3}\overrightarrow {AB} \Leftrightarrow \left\{ \matrix{
\overrightarrow {AM} \uparrow \uparrow \overrightarrow {AB} \hfill \cr 
AM = {2 \over 3}AB \hfill \cr} \right. \cr 
& \overrightarrow {AN} = - {2 \over 3}\overrightarrow {AC} \Leftrightarrow \left\{ \matrix{
\overrightarrow {AN} \uparrow \downarrow \overrightarrow {AC} \hfill \cr 
AN = {2 \over 3}AC \hfill \cr} \right. \cr} \)

Vậy \(M\) thuộc đoạn \(AB\) sao cho \(AM = {2 \over 3}AB \) và \(N\) thuộc tia đối của tia \(AC\) sao cho \(AN = {2 \over 3}AC .\)

LG b

Hãy tìm mối liên hệ giữa \(α, β\) để \(MN//BC\)

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}
\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \beta \overrightarrow {AC} - \alpha \overrightarrow {AB} \\
\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \\
MN//BC \Leftrightarrow \dfrac{\beta }{1} = \dfrac{{ - \alpha }}{{ - 1}} \Leftrightarrow \beta = \alpha
\end{array}\)

Vậy \(MN//BC \Leftrightarrow \beta  = \alpha .\)

HocTot.XYZ