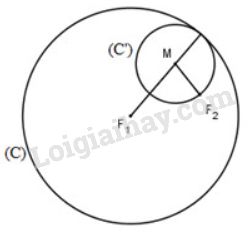
Bài 27 trang 98 SGK Hình học 10Cho đường tròn (C) tâm F1 bán kính 2a và một điểm F2 ở bên trong của (C). Đề bài Cho đường tròn \((C)\) tâm \(F_1\) bán kính \(2a\) và một điểm \(F_2\) ở bên trong của \((C)\). Tập hợp tâm \(M\) của các đường tròn \((C’)\) thay đổi nhưng luôn đi qua \(F_2\) và tiếp xúc với \((C)\) (xem hình) là đường nào sau đây?
A. Đường thẳng B. Đường tròn C. Elip D. Parabol Video hướng dẫn giải Lời giải chi tiết Gọi bán kính của đường tròn \((C’)\) là \(r\) Ta có: \((C’)\) tiếp xúc trong với đường tròn \((C)\) nên \(F_1M = 2a – r\) \(F_2 ∈ (C’)\) nên \(F_2M = r\) Ta có: \(F_1M + F_2M = 2a – r + r = 2a\) Suy ra: Tập hợp tâm \(M\) của đường tròn \((C’)\) là một elip có hai tiêu điểm \(F_1,F_2\) cố định và độ dài trục lớn bằng \(2a\). Vậy chọn C. HocTot.XYZ
|