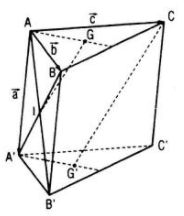
Câu 3 trang 91 SGK Hình học 11 Nâng caoCho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau. Đề bài Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau. Lời giải chi tiết
Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \) Thì \(\overrightarrow {AG} = {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right),\overrightarrow {AI} = {1 \over 2}\left( {\overrightarrow a + \overrightarrow b } \right)\) Do đó, \(\overrightarrow {GI} = \overrightarrow {AI} - \overrightarrow {AG} = {{3\overrightarrow a + \overrightarrow b - 2\overrightarrow c } \over 6}\) Mặt khác : \(\overrightarrow {AG'} = {1 \over 3}\left( {\overrightarrow {AA'} + \overrightarrow {AB'} + \overrightarrow {AC'} } \right) = \overrightarrow a + {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right)\) \( \Rightarrow \overrightarrow {CG'} = \overrightarrow {AG'} - \overrightarrow {AC} = \overrightarrow a + {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right) - \overrightarrow c \) \(= {{3\overrightarrow a + \overrightarrow b - 2\overrightarrow c } \over 3}\) Vậy \(\overrightarrow {CG'} = 2\overrightarrow {GI} .\) Ngoài ra, điểm G không thuộc đường thẳng CG’ nên GI và CG’ là hai đường thẳng song song. HocTot.XYZ
|