Câu 5 trang 50 SGK Hình học 11 Nâng cao

Đề bài

Cho mặt phẳng (P) và ba điểm không thẳng hàng A, B, C cùng nằm ngoài (P). Chứng minh rằng nếu ba đường thẳng AB, BC, CA đều cắt mp (P) thì các giao điểm đó thẳng hàng.

Lời giải chi tiết

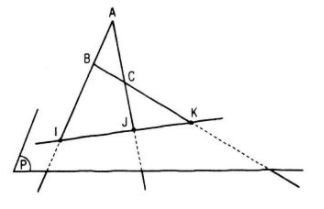
Gọi I, J, K lần lượt là giao điểm của AB, AC, BC với mp(P). A, B, C không thẳng hàng nên có mp(ABC).

Ta có:

$\begin{array}{l} I = AB \cap \left( P \right)\\ \Rightarrow \left\{ \begin{array}{l} I \in AB \subset \left( {ABC} \right)\\ I \in \left( P \right) \end{array} \right.\\ \Rightarrow I \in \left( {ABC} \right) \cap \left( P \right)\,\,\,\left( 1 \right)\\ J = AC \cap \left( P \right)\\ \Rightarrow \left\{ \begin{array}{l} J \in AC \subset \left( {ABC} \right)\\ J \in \left( P \right) \end{array} \right.\\ \Rightarrow J \in \left( {ABC} \right) \cap \left( P \right)\,\,\,\left( 2 \right) \end{array}$

Từ (1) và (2)$\Rightarrow \left( {ABC} \right) \cap \left( P \right) = IJ$

Lại có,

$\begin{array}{l} K = BC \cap \left( P \right)\\ \Rightarrow \left\{ \begin{array}{l} K \in BC \subset \left( {ABC} \right)\\ K \in \left( P \right) \end{array} \right.\\ \Rightarrow K \in \left( {ABC} \right) \cap \left( P \right) = IJ \end{array}$

Vậy I, J, K thẳng hàng.

HocTot.XYZ