Video hướng dẫn giải
Lựa chọn câu để xem lời giải nhanh hơn
Cho tam giác \(OAB\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(OA\) và \(OB\). Tìm các số \(m, n\) sao cho:
LG a
\(\overrightarrow {OM} = m\overrightarrow {OA} + n\overrightarrow {OB} \)
Phương pháp giải:
Biểu diễn \(\overrightarrow {OM} \) qua \(\overrightarrow {OA} ,\overrightarrow {OB} \) suy ra m, n.
Lời giải chi tiết:
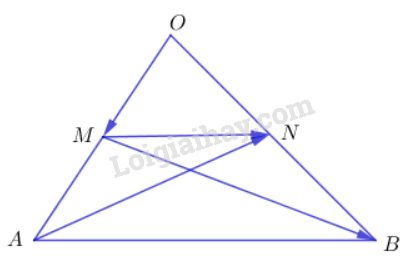
Ta có: M là trung điểm của OA nên:
\(\begin{array}{l}
\overrightarrow {OM} = \frac{1}{2}\overrightarrow {OA} = \frac{1}{2}.\overrightarrow {OA} + 0.\overrightarrow {OB} \\
\Rightarrow m = \frac{1}{2},n = 0
\end{array}\)
Cách trình bày khác:
Ta có: \(\overrightarrow {OM} = {1 \over 2}\overrightarrow {OA} \)
\(\begin{array}{l}
\overrightarrow {OM} = n\overrightarrow {OA} + n\overrightarrow {OB}\\ \Rightarrow m\overrightarrow {OA} + n\overrightarrow {OB} = \frac{1}{2}\overrightarrow {OA} \\
\Leftrightarrow m\overrightarrow {OA} + n\overrightarrow {OB} - \frac{1}{2}\overrightarrow {OA} = \overrightarrow 0 \\
\Leftrightarrow \left( {m - \frac{1}{2}} \right)\overrightarrow {OA} + n\overrightarrow {OB} = \overrightarrow 0 \\
\Leftrightarrow \left\{ \begin{array}{l}
m - \frac{1}{2} = 0\\
n = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m = \frac{1}{2}\\
n = 0
\end{array} \right..
\end{array}\)
Vậy \(m = {1 \over 2}; \, \, n = 0.\)
LG b
\(\overrightarrow {AN} = m\overrightarrow {OA} + n\overrightarrow {OB} \)
Lời giải chi tiết:
Ta có: N là trung điểm OB nên \(\overrightarrow {ON} = \frac{1}{2}\overrightarrow {OB} \).
Khi đó,
\(\begin{array}{l}
\overrightarrow {AN} = \overrightarrow {ON} - \overrightarrow {OA} \\
= \frac{1}{2}\overrightarrow {OB} - \overrightarrow {OA} \\
= \left( { - 1} \right).\overrightarrow {OA} + \frac{1}{2}.\overrightarrow {OB} \\
\Rightarrow m = - 1,n = \frac{1}{2}
\end{array}\)
Cách khác:
Ta có: vì \(N\) là trung điểm \(OB\)
\(\eqalign{
& 2\overrightarrow {AN} = \overrightarrow {AO} + \overrightarrow {AB} \cr
& \Rightarrow 2\overrightarrow {AN} = \overrightarrow {AO} + \overrightarrow {AO} + \overrightarrow {OB} \cr
& \Rightarrow 2\overrightarrow {AN} = 2\overrightarrow {AO} + \overrightarrow {OB}\cr& \Rightarrow \overrightarrow {AN} = - \overrightarrow {OA} + {1 \over 2}\overrightarrow {OB} \cr} \)
\( \Leftrightarrow m\overrightarrow {OA} + n\overrightarrow {OB} = - \overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} \)
\(\Leftrightarrow m\overrightarrow {OA} + n\overrightarrow {OB} + \overrightarrow {OA} - \frac{1}{2}\overrightarrow {OB} = \overrightarrow 0 \)
\(\begin{array}{l}
\Leftrightarrow \left( {m + 1} \right)\overrightarrow {OA} + \left( {n - \frac{1}{2}} \right)\overrightarrow {OB} = \overrightarrow 0 \\
\Leftrightarrow \left\{ \begin{array}{l}
m + 1 = 0\\
n - \frac{1}{2} = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m = - 1\\
n = \frac{1}{2}
\end{array} \right..
\end{array}\)
Vậy \(m = - 1; \, \, n = {1 \over 2}.\)
LG c
\(\overrightarrow {MN} = m\overrightarrow {OA} + n\overrightarrow {OB} \)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}
\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} \\
= \frac{1}{2}\overrightarrow {OB} - \frac{1}{2}\overrightarrow {OA} \\
= - \frac{1}{2}\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} \\
\Rightarrow m = - \frac{1}{2},n = \frac{1}{2}
\end{array}\)
Cách khác:
\(\eqalign{ \, \,& \overrightarrow {MN} = {1 \over 2}\overrightarrow {AB}\cr& \Rightarrow \overrightarrow {MN} = {1 \over 2}(\overrightarrow {AO} + \overrightarrow {OB} ) \cr & \Rightarrow \overrightarrow {MN} = - {1 \over 2}\overrightarrow {OA} + {1 \over 2}\overrightarrow {OB} \cr} \)
\( \Leftrightarrow m\overrightarrow {OA} + n\overrightarrow {OB} = - \frac{1}{2}\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB}\)
\( \Leftrightarrow m\overrightarrow {OA} + n\overrightarrow {OB} + \frac{1}{2}\overrightarrow {OA} - \frac{1}{2}\overrightarrow {OB} = \overrightarrow 0 \)
\(\begin{array}{l}
\Leftrightarrow \left( {m + \frac{1}{2}} \right)\overrightarrow {OA} + \left( {n - \frac{1}{2}} \right)\overrightarrow {OB} = \overrightarrow 0 \\
\Leftrightarrow \left\{ \begin{array}{l}
m + \frac{1}{2} = 0\\
n - \frac{1}{2} = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m = - \frac{1}{2}\\
n = \frac{1}{2}
\end{array} \right..
\end{array}\)
Vậy \(m = - {1 \over 2}, \, \, n = {1 \over 2}.\)
LG d
\(\overrightarrow {MB} = m\overrightarrow {OA} + n\overrightarrow {OB} \)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}
\overrightarrow {MB} = \overrightarrow {OB} - \overrightarrow {OM} \\
= \overrightarrow {OB} - \frac{1}{2}\overrightarrow {OA} \\
= - \frac{1}{2}\overrightarrow {OA} + \overrightarrow {OB} \\
\Rightarrow m = - \frac{1}{2},n = 1
\end{array}\)
Cách khác:
Vì M là trung điểm AO nên ta có:
\(\eqalign{
& 2\overrightarrow {BM} = \overrightarrow {BA} + \overrightarrow {BO}\cr& \Rightarrow 2\overrightarrow {BM} = \overrightarrow {BO} + \overrightarrow {OA} + \overrightarrow {BO} \cr
& \Rightarrow 2\overrightarrow {BM} = 2\overrightarrow {BO} + \overrightarrow {OA}\cr& \Rightarrow 2\overrightarrow {MB} = - \overrightarrow {OA} + 2\overrightarrow {OB} \cr
& \Rightarrow \overrightarrow {MB} = - {1 \over 2}\overrightarrow {OA} + \overrightarrow {OB} \cr} \)
\( \Leftrightarrow m\overrightarrow {OA} + n\overrightarrow {OB} = - \frac{1}{2}\overrightarrow {OA} + \overrightarrow {OB} \)
\(\Leftrightarrow m\overrightarrow {OA} + n\overrightarrow {OB} + \frac{1}{2}\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow 0 \)
\(\begin{array}{l}
\Leftrightarrow \left( {m + {1 \over 2} } \right)\overrightarrow {OA} + \left( {n - 1} \right)\overrightarrow {OB} = \overrightarrow 0 \\
\Leftrightarrow \left\{ \begin{array}{l}
m + \frac{1}{2} = 0\\
n - 1 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m = - \frac{1}{2}\\
n = 1
\end{array} \right..
\end{array}\)
Vậy \(m = - {1 \over 2}, \, \, n = 1.\)
HocTot.XYZ














