Nội dung từ Loigiaihay.Com
Câu hỏi:
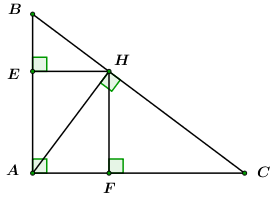
Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH,\,\,AB = 3\,cm,\,\,BC = 6\,cm.\) Gọi \(E,\,\,F\) lần lượt là hình chiếu vuông góc của \(H\) trên \(AB\) và \(AC.\)
Câu 1:
Giải \(\Delta ABC.\)
- A \(\angle B = {45^0};\,\,\,\angle C = {45^0}\)
- B \(\angle B = {60^0};\,\,\,\angle C = {30^0}\)
- C \(\angle B = {30^0};\,\,\,\angle C = {60^0}\)
- D \(\angle B = {35^0};\,\,\,\angle C = {55^0}\)
Phương pháp giải:
Sử dụng định lý Pitago và tỉ số lượng giác của góc nhọn trong tam giác vuông để làm bài.
Lời giải chi tiết:
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại\(A\) ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{6^2} - {3^2}} = \sqrt {27} = 3\sqrt 3 \,\,cm.\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(\begin{array}{l}\cos \angle B = \frac{{AB}}{{BC}} = \frac{3}{6} = \frac{1}{2} \Rightarrow \angle B = {60^0}\\ \Rightarrow \angle C = {90^0} - \angle B = {90^0} - {60^0} = {30^0}.\end{array}\)
Câu 2:
Tính \(AH\) và chứng minh \(EF = AH.\)
- A \(AH = \frac{{3\sqrt 3 }}{2}\,\,cm\)
- B \(AH = 3\sqrt 3 \,\,cm\)
- C \(AH = \frac{{\sqrt 3 }}{2}\,\,cm\)
- D \(AH = \frac{3}{2}\,\,cm\)
Phương pháp giải:
Sử dụng công thức hệ thức lượng trong tam giác vuông để làm bài.
Lời giải chi tiết:
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại\(A\) có đường cao \(AH\) ta có:
\(AH = \frac{{AB.AC}}{{BC}} = \frac{{3.3\sqrt 3 }}{6} = \frac{{3\sqrt 3 }}{2}\,\,cm.\)
Xét tứ giác \(AEHF\) ta có: \(\angle A = \angle E = \angle F = {90^0}\,\,\,\left( {gt} \right)\)
\( \Rightarrow AEHF\) là hình chữ nhật (dhnb).
\( \Rightarrow AH = EF\) (hai đường chéo hình chữ nhật).
Câu 3:
Tính \(EA.EB + AF.FC.\)
- A \(\frac{{81}}{2}\)
- B \(\frac{{81}}{4}\)
- C \(\frac{{27}}{2}\)
- D \(\frac{{27}}{4}\)
Phương pháp giải:
Sử dụng công thức hệ thức lượng trong tam giác vuông để làm bài.
Lời giải chi tiết:
Áp dụng hệ thức lượng cho \(\Delta ABH\) vuông tại \(H\) có đường cao \(HE\) ta có:
\(AH.BC = AB.AC \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{3.3\sqrt 3 }}{6} = \frac{{3\sqrt 3 }}{2}\,\,cm.\)
Áp dụng hệ thức lượng cho \(\Delta ABH\) vuông tại \(H\) có đường cao \(HE\) ta có:
\(H{E^2} = EA.EB\)
Áp dụng hệ thức lượng cho \(\Delta ACH\) vuông tại \(H\) có đường cao \(HF\) ta có:
\(\begin{array}{l}H{F^2} = AF.FC\\ \Rightarrow EB.EA + AF.DC = H{E^2} + H{F^2} = A{H^2} = {\left( {\frac{{3\sqrt 3 }}{2}} \right)^2} = \frac{{27}}{4}\,.\end{array}\)