Dạng 1. Đặc điểm của một số hình phẳng quan trọng Chủ đề 8 Ôn hè Toán 6

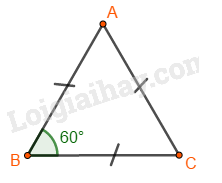
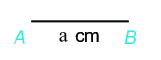
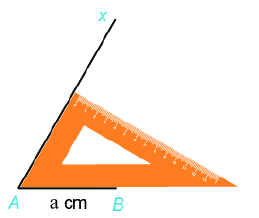
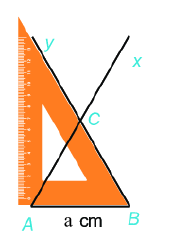
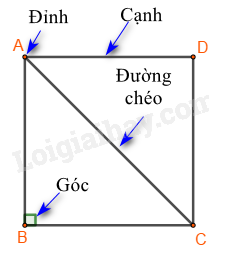
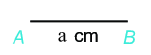
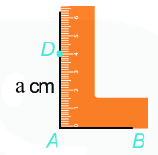
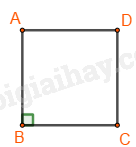
Lý thuyết

1. Hình tam giác đều

a. Các yếu tố cơ bản của tam giác đều:

- Ba cạnh bằng nhau.

- Ba góc bằng nhau và bằng ${60^0}$

b. Cách vẽ tam giác đều ABC khi biết độ dài một cạnh bằng a.

Bước 1: Vẽ đoạn thẳng $AB = a$.

Bước 2: Dùng ê ke có góc ${60^0}$, vẽ góc BAx bằng ${60^0}$.

Bước 3: Vẽ góc $ABy = {60^0}$ hai tia Ax,By cắt nhau tại $C$, ta được tam giác đều ABC

2. Hình vuông

a. Một số yếu tố cơ bản của hình vuông

- Bốn cạnh bằng nhau.

- Bốn góc bằng nhau và bằng ${90^0}$.

- Hai đường chéo bằng nhau.

b. Cách vẽ hình vuông khi biết độ dài cạnh bằng $a$:

Bước 1: Vẽ đoạn thẳng $AB = a\left( {cm} \right)$

Bước 2: Vẽ đường thẳng vuông góc với AB tại $A$. Xác định điểm $D$ trên đường thẳng đó sao cho $AD = a\left( {cm} \right)$.

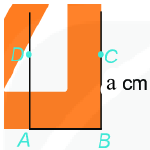
Bước 3: Vẽ đường thẳng vuông góc với AB tại $B$. Xác định điểm $C$ trên đường thẳng đó sao cho $BC = a\left( {cm} \right)$.

Bước 4: Nối $C$ với $D$ ta được hình vuông ABCD.

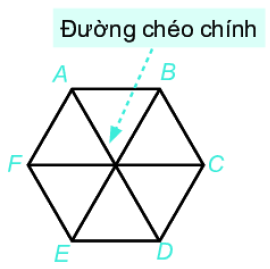
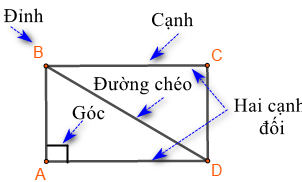
3. Hình lục giác đều

Một số yếu tố cơ bản của hình lục giác đều:

- Sáu cạnh bằng nhau.

- Sáu góc bằng nhau và bằng ${120^0}$.

- Ba đường chéo chính bằng nhau.

- AC, BD, CE, DF, EA,FB là các đường chéo phụ của ABCDEF.

4. Hình chữ nhật

a. Nhận biết hình chữ nhật

Một số yếu tố cơ bản của hình chữ nhật

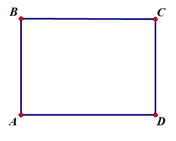
- Bốn góc bằng nhau và bằng ${90^0}$

- Các cạnh đối bằng nhau.

- Hai đường chéo bằng nhau.

b.Cách vẽ hình chữ nhật

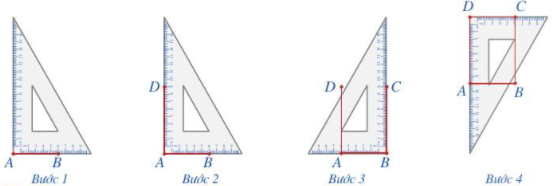
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng a cm

Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng b cm

Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng b cm

Bước 4. Vẽ đoạn thẳng CD.

5. Hình thoi

a. Một số yếu tố cơ bản của hình thoi

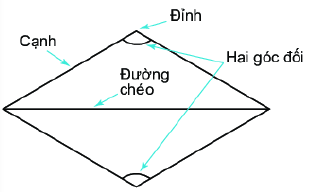
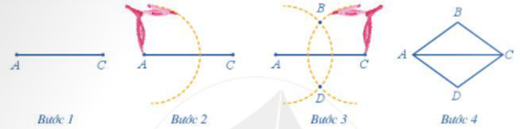
- Bốn cạnh bằng nhau

- Hai đường chéo vuông góc với nhau.

- Các cạnh đối song song với nhau

- Các góc đối bằng nhau

b. Vẽ hình thoi

Ví dụ: Dùng thước và compa vẽ hình thoi $ABCD$, biết $AB = 5{\mkern 1mu} cm$ và $AC = 8{\mkern 1mu} cm$.

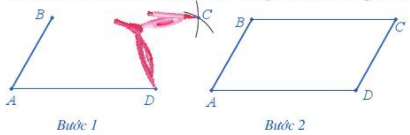
Bước 1. Dùng thước vẽ đoạn thẳng $AC = 8{\mkern 1mu} cm$

Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính $5{\mkern 1mu} cm$.

Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính $5{\mkern 1mu} cm$; phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.

Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA.

6. Hình bình hành

a. Nhận biết hình bình hành

Hình bình hành ABCD có:

- Bốn đỉnh A, B, C, D.

- Hai cặp cạnh đối diện bằng nhau: $AB = CD;{\mkern 1mu} BC = AD$.

- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: OA = OC; OB = OD.

- Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.

.b. Cách vẽ hình bình hành

Ví dụ: Cho trước hai đoạn thẳng AB, AD như hình dưới đây. Vẽ hình bình hành ABCD nhận hai đoạn thẳng AB, AD làm cạnh.

Cách vẽ:

Ta có thể vẽ bằng thước và compa như sau:

Bước 1. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AD. Lấy D làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai phần đường tròn này

Bước 2. Dùng thước vẽ các đoạn thẳng BC và CD.

7. Hình thang cân

a. Nhận biết hình thang cân

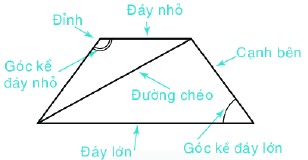
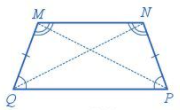
Hình thang cân có: 

- Hai cạnh bên bằng nhau.

- Hai đường chéo bằng nhau

- Hai đáy song song với nhau

- Hai góc kề một đáy bằng nhau.

Ví dụ:

Hình thang cân MNPQ có:

- Hai cạnh cạnh đáy song song: MN song song với PQ.

- Hai cạnh bên bằng nhau: MQ = NP.

- Hai đường chéo bằng nhau: MP = NQ.

.- Hai góc kề với cạnh cạnh bên PQ bằng nhau, tức là hai góc NPQ và PQM bằng nhau; hai góc kề với cạnh bên MN bằng nhau, tức là hai góc QMN và MNP bằng nhau.

b. Cách gấp hình thang cân

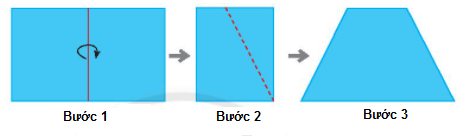
Bước 1: Gấp đôi một tờ giấy hình chữ nhật

Bước 2: Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (Cạnh không chứa nếp gấp). Cắt theo đường nét đứt như hình minh họa.

Bước 3: Mở tờ giấy ra ta được một hình thang cân.

Bước 3: Vẽ đường thẳng vuông góc với AB tại . Xác định điểm  trên đường thẳng đó sao cho .

Bước 4: Nối  với  ta được hình vuông ABCD.

3. Hình lục giác đều

Một số yếu tố cơ bản của hình lục giác đều:

- Sáu cạnh bằng nhau.

- Sáu góc bằng nhau và bằng .

- Ba đường chéo chính bằng nhau.

- AC, BD, CE, DF, EA,FB là các đường chéo phụ của ABCDEF.

4. Hình chữ nhật

a. Nhận biết hình chữ nhật

Một số yếu tố cơ bản của hình chữ nhật

- Bốn góc bằng nhau và bằng 

- Các cạnh đối bằng nhau.

- Hai đường chéo bằng nhau.

b.Cách vẽ hình chữ nhật

Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng a cm

Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng b cm

Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng b cm

Bước 4. Vẽ đoạn thẳng CD.

5. Hình thoi

a. Một số yếu tố cơ bản của hình thoi

- Bốn cạnh bằng nhau

- Hai đường chéo vuông góc với nhau.

- Các cạnh đối song song với nhau

- Các góc đối bằng nhau

b. Vẽ hình thoi

Ví dụ: Dùng thước và compa vẽ hình thoi $ABCD$, biết  và .

Bước 1. Dùng thước vẽ đoạn thẳng

Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính .

Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính ; phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.

Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA.

6. Hình bình hành

a. Nhận biết hình bình hành

Hình bình hành ABCD có:

- Bốn đỉnh A, B, C, D.

- Hai cặp cạnh đối diện bằng nhau: .

- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: OA = OC; OB = OD.

- Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.

.b. Cách vẽ hình bình hành

Ví dụ: Cho trước hai đoạn thẳng AB, AD như hình dưới đây. Vẽ hình bình hành ABCD nhận hai đoạn thẳng AB, AD làm cạnh.

Cách vẽ:

Ta có thể vẽ bằng thước và compa như sau:

Bước 1. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AD. Lấy D làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai phần đường tròn này

Bước 2. Dùng thước vẽ các đoạn thẳng BC và CD.

7. Hình thang cân

a. Nhận biết hình thang cân

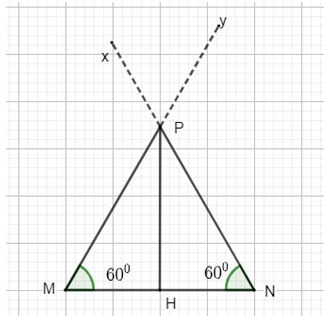
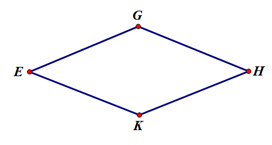
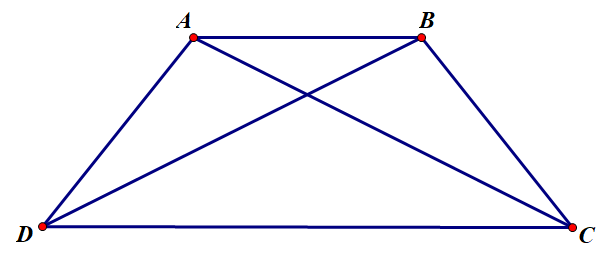
Hình thang cân có: 

- Hai cạnh bên bằng nhau.

- Hai đường chéo bằng nh

Bài tập

Bài 1:

a) Vẽ tam giác $MNP$ đều có $MN = 4cm$

b) Xác định điểm $H$ trên cạnh $MN$ sao cho $MH = 2cm$

c) Dùng thước đo góc đo các góc của tam giác $PMH$

d) Các tam giác $PHM$ và tam giác $PHN$ có phải các tam giác đều không? Vì sao?

Bài 2:

Tổng các góc trong một hình lục giác đều luôn gấp mấy lần tổng các góc trong một hình vuông?

Bài 3:

Cho hình chữ nhật $ABCD$ có $AB = 3cm;\,AD = 4cm;\,AC = 5cm$. Tính độ dài của cạnh $CD,BC,BD$.

Bài 4:

Cho hình thoi $EGHK$ với $O$ là giao điểm của hai đường chéo. Biết $EG = 15cm$. Tính $GH,HK,KE$?

Bài 5:

Cho hình thang cân $ABCD$$\left( {AB//CD} \right)$ có $AB = 6cm$, $AD = 8cm$, $AC = 11cm$, $\angle BCD = {40^0}$. Tính $BD$; $\angle ADC$. 

Lời giải chi tiết:

Bài 1:

a) Vẽ tam giác $MNP$ đều có $MN = 4cm$

b) Xác định điểm $H$ trên cạnh $MN$ sao cho $MH = 2cm$

c) Dùng thước đo góc đo các góc của tam giác $PMH$

d) Các tam giác $PHM$ và tam giác $PHN$ có phải các tam giác đều không? Vì sao?

Phương pháp

Vẽ tam giác đều thông qua vẽ đoạn thẳng khi biết độ dài và vẽ góc khi biết số đo góc

Sử dụng thước đo góc để đo góc

Sử dụng tính chất về góc để nhận biết tam giác đều.

Lời giải

a)

Bước 1: Vẽ $MN = 4cm$ bằng thước thẳng

Bước 2: Vẽ $\angle MNx = {60^0}$ và $\angle NMy = {60^0}$ bằng thước êkê có góc ${60^0}$

Bước 3: Hai tia $My$ và $Nx$ cắt nhau tại $P$ ta được tam giác $MNP$

b)

Trên đoạn  $MN$ lấy điểm $H$ sao cho $MH = 2cm$

c) Đo được $\angle PHM = {90^0}$ và $\angle PHN = {90^0}$

d) Tam giác $PHM$ và tam giác $PHN$ không phải là các tam giác đều vì mỗi tam giác đều tồn tại một góc không bằng ${60^0}$. 

Bài 2:

Tổng các góc trong một hình lục giác đều luôn gấp mấy lần tổng các góc trong một hình vuông?

Phương pháp

Sử dụng khái niệm hình vuông, hình lục giác đều

Lời giải

Trong hình vuông có: bốn góc bằng nhau và bằng ${90^0}$, nên tổng các góc của hình vuông bằng ${4.90^0} = {360^0}$

Trong một hình lục giác đều, có sáu góc bằng nhau, mỗi góc có số đo bằng ${120^0}$ nên  tổng các góc trong một hình lục giác đều là ${6.120^0} = {720^0}$.

Vậy tổng các góc trong một hình lục giác đều luôn gấp $\dfrac{{{{720}^0}}}{{{{360}^0}}} = 2$ lần tổng các góc trong một hình vuông.

Bài 3:

Cho hình chữ nhật $ABCD$ có $AB = 3cm;\,AD = 4cm;\,AC = 5cm$. Tính độ dài của cạnh $CD,BC,BD$.

Phương pháp

Áp dụng được mối quan hệ giữa các yếu tố của hình chữ nhật vào giải toán.

Lời giải

Ta có: $ABCD$ là hình chữ nhật

$AD = BC = 4cm\,$

            $CD = AB = 3cm$

     $BD = AC = 5cm$

Bài 4:

Cho hình thoi $EGHK$ với $O$ là giao điểm của hai đường chéo. Biết $EG = 15cm$. Tính $GH,HK,KE$?

Phương pháp

Sử dụng định nghĩa của hình thoi có 4 cạnh bằng nhau nên tính được độ dài của các cạnh

Lời giải

Ta có: $EGHK$ là hình thoi

$\Rightarrow GH = HK = KE = EG = 15cm$

Bài 5:

Cho hình thang cân $ABCD$$\left( {AB//CD} \right)$ có $AB = 6cm$, $AD = 8cm$, $AC = 11cm$, $\angle BCD = {40^0}$. Tính $BD$; $\angle ADC$.

Phương pháp

Áp dụng phát biểu "Hình thang cân có hai góc kề một đáy bằng nhau" và "Hình thang cân có hai đường chéo bằng nhau" để giải toán.

Lời giải

Ta có: $BD = AC = 11cm;\angle ADC = \angle BCD = {40^0}$