Đề cương bài tập học kỳ II môn toán lớp 12Tổng hợp kiến thức cần nắm vững, các dạng bài tập và câu hỏi có khả năng xuất hiện trong đề thi HK2 Toán học 12 sắp tới
Lựa chọn câu để xem lời giải nhanh hơn
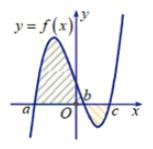
Phần 1 Nguyên hàm Câu 1. Cho \(y = f\left( x \right),y = g\left( x \right)\)là các hàm số liên tục trên \(\mathbb{R}\). Tìm khẳng định sai trong các khẳng định sau: A. \(\int {k.f\left( x \right)dx} = k.\int {f\left( x \right)dx} \) với \(k \in \mathbb{R}\backslash \left\{ 0 \right\}\) B. \(\int {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} + \int {g\left( x \right)dx} \) C. \(\int {\left[ {f\left( x \right).g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} .\int {g\left( x \right)dx} \) D. \(\left[ {\int {f\left( x \right)dx} } \right]' = f\left( x \right)\). Câu 2. \(F\left( x \right)\) là một nguyên hàm của hàm số \(y = x.{e^{{x^2}}}\). Hàm số nào sau đây không phải là \(F\left( x \right)\)? A. \(F\left( x \right) = \frac{1}{2}{e^{{x^2}}} + 2\) B. \(F\left( x \right) = \frac{1}{2}\left( {{e^{{x^2}}} + 5} \right)\) C. \(F\left( x \right) = - \frac{1}{2}{e^{{x^2}}} + C\) D. \(F\left( x \right) = - \frac{1}{2}\left( {2 - {e^{{x^2}}}} \right)\) Câu 3. Cho hai hàm số \(F\left( x \right) = \left( {{x^2} + ax + b} \right).{e^{ - x}}\) và \(f\left( x \right) = \left( { - {x^2} + 3x + 6} \right).{e^{ - x}}\). Tìm a và b để \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\). A. a = 1, b = -7 B. a = - 1, b = - 7 C. a = - 1 , b = 7 D. a = 1, b = 7. Câu 4. \(F\left( x \right) = \left( {a{x^3} + b{x^2} + cx + d} \right).{e^{ - x}} + 2018e\) là một nguyên hàm của hàm số \(f\left( x \right) = \left( { - 2{x^3} + 3{x^2} + 7x - 2} \right){e^{ - x}}\). Khi đó: A. \(a + b + c + d = 4\) B. \(a + b + c + d = 5\) C. \(a + b + c + d = 6\) D. \(a + b + c + d = 7\) Câu 5. Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{3}{{{x^2}}}\) là: A. \(\int {f\left( x \right)dx} = 3\ln {x^2} + C\) B. \(\int {f\left( x \right)dx} = - \frac{3}{x} + C\) C. \(\int {f\left( x \right)dx} = \frac{3}{{{x^2}}} + C\) D. \(\int {f\left( x \right)dx} = \frac{3}{x} + C\) Câu 6. Hàm số \(F\left( x \right) = \tan x + 2\) là một nguyên hàm của hàm số nào dưới đây? A. \(f\left( x \right) = - \frac{1}{{{{\sin }^2}x}}\) B. \(f\left( x \right) = \frac{1}{{{{\sin }^2}x}}\) C. \(f\left( x \right) = \frac{1}{{{{\cos }^2}x}}\) D. \(f\left( x \right) = - \frac{1}{{{{\cos }^2}x}}\) Câu 7. Tìm \(\int {\left( {1 - x} \right)\cos xdx} \) A. \(\int {\left( {1 - x} \right)\cos xdx} = \left( {1 - x} \right)\sin x - \cos x + C\) B. \(\int {\left( {1 - x} \right)\cos xdx} = \left( {1 + x} \right)\sin x - \cos x + C\) C. \(\int {\left( {1 - x} \right)\cos xdx} = \left( {1 - x} \right)\sin x + \cos x + C\) D. \(\int {\left( {1 - x} \right)\cos xdx} = \left( {1 - x} \right)\sin x - \sin x + C\) Câu 8. Biết \(\int {f\left( x \right)dx} = 2x\ln \left( {3x - 1} \right) + C\). Tìm khẳng định đúng trong các khẳng định sau: A. \(\int {f\left( {3x} \right)dx} = 6x\ln \left( {3x - 1} \right) + C\) B. \(\int {f\left( {3x} \right)dx} = 6x\ln \left( {3x - 1} \right) + C\) C. \(\int {f\left( {3x} \right)dx} = 3x\ln \left( {9x - 1} \right) + C\) D. \(\int {f\left( {3x} \right)dx} = 2x\ln \left( {9x - 1} \right) + C\) Câu 9. Tìm nguyên hàm \(\int {\frac{{2{x^3} - 6{x^2} + 4x + 1}}{{{x^2} - 3x + 2}}} dx\) A. \({x^2} + \ln \left| {\frac{{x - 1}}{{x - 2}}} \right| + C\) B. \(\frac{1}{2}{x^2} + \ln \left| {\frac{{x - 2}}{{x - 1}}} \right| + C\) C. \(\frac{1}{2}{x^2} + \ln \left| {\frac{{x - 1}}{{x - 2}}} \right| + C\) D. \({x^2} + \ln \left| {\frac{{x - 2}}{{x - 1}}} \right| + C\) Câu 10. Tìm nguyên hàm \(\int {\frac{{2x - 1}}{{{{\left( {x + 1} \right)}^2}}}dx} \) A. \(2\ln \left| {x + 1} \right| - \frac{3}{{x + 1}} + C\) B. \(2\ln \left| {x + 1} \right| + \frac{3}{{x + 1}} + C\) C. \( - \ln \left| {x + 1} \right| + \frac{3}{{x + 1}} + C\) D. \(\ln \left| {\frac{{x - 1}}{{x + 1}}} \right| + C\). Câu 11. Tính \(\int {\frac{{dx}}{{\sqrt {1 - x} }}} \) thu được kết quả là: A. \(\frac{C}{{\sqrt {1 - x} }}\) B. \( - 2\sqrt {1 - x} + C\) C. \(\frac{2}{{\sqrt {1 - x} }} + C\) D. \(\sqrt {1 - x} + C\) Câu 12. Cho \(\int {\frac{{dx}}{{\sqrt {x + 2} + \sqrt {x + 1} }} = a\left( {x + 2} \right)\sqrt {x + 2} + b\left( {x + 1} \right)\sqrt {x + 1} + C} \). Khi đó 3a+b bằng: A. \( - \frac{2}{3}\) B. \(\frac{1}{3}\) C. \(\frac{4}{3}\) D. \(\frac{2}{3}\) Câu 13. Họ nguyên hàm của hàm số \(f\left( x \right) = {\cos ^2}2x\) là: A. \(\frac{1}{2} + \frac{{\sin 4x}}{8} + C\) B. \(\frac{x}{2} - \frac{{\sin 4x}}{2} + C\) C. \(\frac{1}{2} - \frac{{\sin 4x}}{2} + C\) D. \(\frac{x}{2} + \frac{{\sin 4x}}{8} + C\) Câu 14. Họ nguyên hàm của hàm số \(f\left( x \right) = {\tan ^2}x\) là: A. \(\cot x - x + C\) B. \(\tan x - x + C\) C. \( - \cot x - x + C\) D. \( - \tan x - x + C\). Câu 15. Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{1}{{\sin x}}\) là: A. \(\ln \left| {\cot \frac{x}{2}} \right| + C\) B. \(\ln \left| {\tan \frac{x}{2}} \right| + C\) C. \( - \ln \left| {\tan \frac{x}{2}} \right| + C\) D. \(\ln \left| {\sin x} \right| + C\). Câu 16. Họ nguyên hàm của hàm số \(f\left( x \right) = 2x.{x^{{x^2}}}\) là: A. \(\frac{1}{{{2^{{x^2}}}\ln 2}} + C\) B. \(\frac{1}{{\ln 2}}{2^{{x^2}}} + C\) C. \(\frac{{\ln 2}}{{{2^{{x^2}}}}} + C\) D. \({2^{{x^2}}}\ln 2 + C\). Câu 17. Tìm \(\int {{e^{{{\sin }^2}x}}\sin 2xdx} \)? A. \({e^{{{\sin }^2}x}} + C\) B. \(\sin x{e^{\tan x}} + C\) C. \({e^{\tan x}} + C\) D. \({e^{\sin 2x}} + C\) Câu 18. Họ nguyên hàm của hàm số \(f\left( x \right) = x.\sqrt[3]{{3x - 1}}\) là: A. \(\frac{1}{{21}}\sqrt[3]{{{{\left( {3x - 1} \right)}^7}}} + \frac{1}{{15}}\sqrt[3]{{{{\left( {3x - 1} \right)}^5}}} + C\) B. \(\frac{1}{{18}}\sqrt[3]{{{{\left( {3x - 1} \right)}^6}}} + \frac{1}{{12}}\sqrt[3]{{{{\left( {3x - 1} \right)}^4}}} + C\) C. \(\frac{1}{9}\sqrt[3]{{{{\left( {3x - 1} \right)}^3}}} + \sqrt[3]{{3x - 1}} + C\) D. \(\frac{1}{{12}}\sqrt[3]{{{{\left( {3x - 1} \right)}^4}}} + \frac{1}{3}\sqrt[3]{{3x - 1}} + C\) Câu 19. Tìm \(T = \int {\frac{{dx}}{{\cos x.{{\sin }^3}x}}} \) A. \( - \ln \left| {\cot x} \right| - \frac{1}{2}{\cot ^2}x + C\) B. \( - \ln \left| {\sin x} \right| - \frac{1}{2}\cot x + C\) C. \( - \ln \left| {\cot x} \right| + {\cot ^2}x + C\) D. \( - \ln \left| {\tan x} \right| - \frac{1}{2}{\cot ^2}x + C\) Câu 20. Họ nguyên hàm của hàm số \(f\left( x \right) = {x^2}.{e^{{x^3} + 1}}\) là: A. \(\arcsin \frac{x}{2} - \frac{{x\sqrt {4 - {x^2}} }}{4} + C\) B. \(2\arccos \frac{x}{2} - \frac{{x\sqrt {4 - {x^2}} }}{2} + C\) C. \(\arccos \frac{x}{2} - \frac{{x\sqrt {4 - {x^2}} }}{4} + C\) D. \(2\arcsin \frac{x}{2} - \frac{{x\sqrt {4 - {x^2}} }}{2} + C\) Phần 2 Tích phân Câu 1. Cho \(\int\limits_0^2 {f\left( x \right)dx} = - 1,\int\limits_0^2 {g\left( x \right)dx} = 1\). Khi đó \(\int\limits_0^2 {\left[ {f\left( x \right) + g\left( x \right) + 1} \right]dx} \) bằng: A. 1 B. 4 C. 2 D. 0 Câu 2. Biết rằng \(\int\limits_0^{\frac{\pi }{4}} {x\cos 2xdx} = \frac{\pi }{a} + \frac{1}{b}\), với \(a,b \in \mathbb{Z}\). Khẳng định nào sau đây đúng? A. \(a + b = 4\) B. \(a + b = 3\) C. \(a + b = - 1\) D. \(a + b = 1\) Câu 3. Biết \(F\left( x \right)\) là nguyên hàm của hàm số \(f\left( x \right) = 4{x^3} - \frac{1}{{{x^2} + 3x}}\) và thỏa mãn \(F\left( 1 \right) + 2F\left( 2 \right) = 2\). Tính \(F\left( 2 \right)\) A. \(F\left( 2 \right) = 38\) B. \(F\left( 2 \right) = \frac{{86}}{7}\) C. \(F\left( 2 \right) = 7\) D. \(F\left( 2 \right) = \frac{{151}}{4}\) Câu 4. Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(f\left( {3x} \right) = 2f\left( x \right)\), với \(\forall x \in \mathbb{R}\). Biết rằng \(\int\limits_0^2 {f\left( x \right)dx} = 2\). Giá trị của tích phân \(\int\limits_0^6 {f\left( x \right)dx} \) bằng: A. 4 B. 2 C. 6 D. 12 Câu 5. Cho hàm số \(f\left( x \right)\) có đạo hàm tại \(\forall x \in \mathbb{R}\) và \(f\left( x \right) > 0,\forall x \in \mathbb{R}\). Biết \(f'\left( x \right) = f\left( x \right).{e^x}\) và \(f\left( 1 \right) = e\). Tính \(J = \int\limits_0^2 {\ln \left[ {f\left( x \right)} \right]dx} \). A. \(J = {e^2} - 2e + 1\) B. \(J = {e^2} - 2e - 1\) C. \(J = {e^2} - e + 1\) D. \(J = {e^4} - 2e - 1\) Câu 6. Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\) thỏa \(f'\left( x \right) = \frac{1}{{x - 1}};f\left( 0 \right) = 1;f\left( 2 \right) = 2\). Tính \(f\left( { - 3} \right) + f\left( 3 \right)\). A. \(2 + 3\ln 2\) B. \(1 + 3\ln 2\) C. \(3 + 3\ln 2\) D. \(4 + 3\ln 2\) Câu 7. Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\). Khi đó hiệu số \(F\left( - \right) - F\left( 1 \right)\) bằng: A. \(\int\limits_0^1 {f\left( x \right)dx} \) B. \(\int\limits_0^1 { - F\left( x \right)dx} \) C. \(\int\limits_0^1 {F\left( x \right)dx} \) D. \(\int\limits_0^1 { - f\left( x \right)dx} \) Câu 8. Tính tích phân \(I = \int\limits_0^1 {{x^{2018}}\left( {1 + x} \right)dx} \) A. \(I = \frac{1}{{2018}} + \frac{1}{{2019}}\) B. \(I = \frac{1}{{2020}} + \frac{1}{{2021}}\) C. \(I = \frac{1}{{2019}} + \frac{1}{{2020}}\) D. \(I = \frac{1}{{2017}} + \frac{1}{{2018}}\) Câu 9. Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\frac{2}{{x + 1}}{\rm{ khi }}0 \le x \le 1\\2x - 1{\rm{ khi 1}} \le {\rm{x}} \le {\rm{3}}\end{array} \right.\). Tính tích phân \(\int\limits_0^3 {f\left( x \right)dx} \). A. \(6 + \ln 4\) B. \(4 + \ln 4\) C. \(6 + \ln 2\) D. \(2 + 2\ln 2\) Câu 10. Biết \(\int\limits_{\frac{1}{3}}^1 {\frac{{x - 5}}{{2x + 2}}dx} = a + \ln b\), với a, b là các số thực. Mệnh đề nào dưới đây đúng? A. \(ab = \frac{8}{{81}}\) B. \(a + b = \frac{7}{{24}}\) C. \(ab = \frac{9}{8}\) D. \(a + b = \frac{3}{{10}}\) Câu 11. Tính tích phân \(\int\limits_1^2 {\frac{{ax + 1}}{{{x^2} + 3x + 2}}dx} = \frac{3}{5}\ln \frac{4}{3} + \frac{3}{5}\ln \frac{2}{3}\). Giá trị của a là: A. \(a = \frac{1}{5}\) B. \(a = \frac{2}{5}\) C. \(a = \frac{3}{5}\) D. \(a = \frac{4}{5}\) Câu 12. Cho \(\int\limits_0^1 {\frac{x}{{\sqrt {3x + 1} + \sqrt {2x + 1} }}dx} = \frac{{a + b\sqrt 3 }}{9}\), với a, b là các số thực. Tính tổng \(T = a + b\) A. \(T = - 10\) B. \(T = - 4\) C. \(T = 15\) D. \(T = 8\) Câu 13. Biết \(\int\limits_0^{\frac{\pi }{6}} {\left( {3 + 4{{\sin }^2}x} \right)dx} = \frac{{a\pi }}{b} - \frac{{c\sqrt 3 }}{6}\), trong đó a, b nguyên dương và \(\frac{a}{b}\) tối giản. Tính a+b+c. A. 8 B. 16 C. 12 D. 14 Câu 14. Cho \(F\left( x \right) = \int\limits_0^{{x^2}} {{e^{{t^2}}}dt} \). Tính \(F'\left( 2 \right)\). A. \(F'\left( 2 \right) = 4{e^4}\) B. \(F'\left( 2 \right) = 8{e^{16}}\) C. \(F'\left( 2 \right) = 4{e^{16}}\) D. \(F'\left( 2 \right) = {e^4}\) Câu 15. Cho hàm số \(g\left( x \right) = \int\limits_x^{{x^2}} {\frac{1}{{\ln t}}dt} \) với \(x > 0\). Đạo hàm của \(g\left( x \right)\) là: A. \(g'\left( x \right) = \frac{{x - 1}}{{\ln x}}\) B. \(g'\left( x \right) = \frac{{1 - x}}{{\ln x}}\) C. \(g'\left( x \right) = \frac{1}{{\ln x}}\) D. \(g'\left( x \right) = \ln x\) Câu 16. Trong các tích phân sau, tích phân nào có cùng giá trị với \(I = \int\limits_1^2 {{x^3}\sqrt {{x^2} - 1} dx} \) A. \(\frac{1}{2}\int\limits_1^2 {t\sqrt {t - 1} dt} \) B. \(\int\limits_1^4 {t\sqrt {t - 1} dt} \) C. \(\int\limits_0^{\sqrt 3 } {t\sqrt {t - 1} dt} \) D. \(\int\limits_1^{\sqrt 3 } {\left( {{x^2} + 1} \right){x^2}dt} \) Câu 17. Giả sử \(I = \int\limits_1^{64} {\frac{{dx}}{{\sqrt x + \sqrt[3]{x}}}} = a\ln \frac{2}{3} + b\) với a, b là số nguyên. Tính giá trị \(a - b\). A. \( - 17\) B. \(5\) C. \( - 5\) D. \(17\) Câu 18. Tính tích phân \(I = \int\limits_0^{\frac{\pi }{3}} {\frac{{\sin x}}{{{{\cos }^3}x}}dx} \). A. \(I = \frac{5}{2}\) B. \(I = \frac{3}{2}\) C. \(I = \frac{\pi }{3} + \frac{9}{{20}}\) D. \(I = \frac{9}{4}\) Câu 19. Cho \(I = \int\limits_0^1 {x.{e^{1 - {x^2}}}dx} \). Biết rằng \(I = \frac{{ae - b}}{2}\). Khi đó \(a + b\) bằng: A. \(1\) B. 0 C. 2 D. 4 Câu 20. Biết \(\int\limits_1^2 {\frac{{x + 1}}{{{x^2} + x\ln x}}dx} = \ln \left( {\ln a + b} \right)\) với a, b là các số nguyên dương. Tính \(P = {a^2} + {b^2} + ab\). A. 10 B. 8 C. 12 D. 6 Phần 3 Ứng dụng tích phân tính diện tích, thể tích. Câu 1. Viết công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục Ox và các đường thẳng \(x = a,x = b\left( {a < b} \right)\). A. \(\int\limits_a^b {\left| {f\left( x \right)} \right|dx} \) B. \(\int\limits_a^b {{f^2}\left( x \right)dx} \) C. \(\int\limits_a^b {f\left( x \right)dx} \) D. \(\pi \int\limits_a^b {f\left( x \right)dx} \) Câu 2. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ bên dưới.
Hình phẳng được đánh dấu trong hình vẽ bên có diện tích là: A. \(\int\limits_a^b {f\left( x \right)dx} - \int\limits_b^c {f\left( x \right)dx} \) B. \(\int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} \) C. \( - \int\limits_a^b {f\left( x \right)dx} + \int\limits_b^c {f\left( x \right)dx} \) D. \(\int\limits_a^b {f\left( x \right)dx} - \int\limits_c^b {f\left( x \right)dx} \) Câu 3. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^2} + x - 2\) và trục hoành bằng: A. 9 B. \(\frac{{13}}{6}\) C. \(\frac{9}{2}\) D. \(\frac{3}{2}\) Câu 4. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3} - 3{x^2}\), trục hoành và hai đường thẳng \(x = 1,x = 4\)là: A. \(\frac{{53}}{4}\) B. \(\frac{{51}}{4}\) C. \(\frac{{49}}{4}\) D. \(\frac{{25}}{2}\) Câu 5. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \frac{{x + 1}}{{x - 2}}\) và các trục tọa độ Ox, Oy ta được \(S = a\ln \frac{b}{c} - 1\). Chọn đáp án đúng? A. \(a + b + c = 8\) B. \(a > b\) C. \(a - b + c = 1\) D. \(a + 2b - 9 = c\) Câu 6. Biết diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = 3{x^2} + 2mx + {m^2} + 1\), trục hoành, trục tung và đường thẳng \(x = \sqrt 2 \) đạt giá trị nhỏ nhất. Mệnh đề nào sau đây đúng? A. \(m \in \left( { - 4; - 1} \right)\) B. \(m \in \left( {3;5} \right)\) C. \(m \in \left( {0;3} \right)\) D. \(m \in \left( { - 2;1} \right)\) Câu 7. Cho (H) là hình phẳng được giới hạn bởi các đường \(y = \sqrt x ,y = x - 2\) và trục hoành. Diện tích của (H) bằng: A. \(\frac{7}{3}\) B. \(\frac{8}{3}\) C. \(\frac{{10}}{3}\) D. \(\frac{{16}}{3}\) Câu 8. Diện tích hình phẳng được giới hạn bởi các đường thẳng \(y = \left\{ \begin{array}{l} - x{\rm{ khi }}x \le 1\\x - 2{\rm{ khi }}x > 1\end{array} \right.\) và \(y = \frac{{10}}{3}x - {x^2}\) là \(\frac{a}{b}\). Khi đó \(a + 2b\) bằng: A. 16 B.15 C. 17 D. 18 Câu 9. Cho (H) là hình phẳng được giới hạn bởi parabol \(y = \frac{{\sqrt 3 }}{2}{x^2}\) và đường Elip có phương trình \(\frac{{{x^2}}}{4} + {y^2} = 1\). Diện tích của (H) bằng A. \(\frac{{2\pi + \sqrt 3 }}{6}\) B. \(\frac{{2\pi }}{3}\) C. \(\frac{{\pi + \sqrt 3 }}{4}\) D. \(\frac{{3\pi }}{4}\) Câu 10. Diện tích hình phẳng được giới hạn bởi đồ thị hai hàm số \(x - {y^3} + 1 = 0,x + y - 1 = 0\) là A. \(\frac{5}{4}\) B. \(\frac{1}{3}\) C. \(\sqrt 2 \) D. Đáp án khác Câu 11. Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^4} - 5{x^2} + 4\), trục hoành và hai đường thẳng \(x = 0,x = 1\). A. \(\frac{7}{3}\) B. \(\frac{8}{5}\) C. \(\frac{{64}}{{25}}\) D. \(\frac{{38}}{{15}}\) Câu 12. Cho D giới hạn bởi các đường cong \(y = \sqrt {{x^2} + 1} \), trục hoành và các đường thẳng \(x = 0,x = 1\). Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu? A. \(V = \frac{4}{3}\) B. \(V = 2\pi \) C. \(V = \frac{{4\pi }}{3}\) D. \(V = 2\). Câu 13. Cho hình cong (H) giới hạn bởi đường \(y = {e^x}\), trục hoành và các đường thẳng \(x = 0,x = \ln 4\). Đường thẳng x=k (0< x< ln4) chia (H) thành hai phần có diện tích là \({S_1}\) và \({S_2}\) như hình vẽ bên.
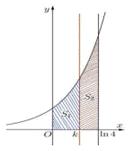
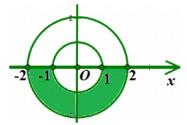
Tìm k để \({S_1} = 2{S_2}\). A. \(k = \frac{2}{3}\ln 4\) B. \(k = \ln 2\) C. \(k = \ln \frac{8}{3}\) D. \(k = \ln 3\) Câu 14. Diện tích hình phẳng giới hạn bởi các đường \(y = {x^2} - 1\) và \(y = - {x^2} + 2x + 3\) không được tính bằng công thức nào sau đây? A. \(S = \int\limits_2^{ - 1} {\left( {2{x^2} - 2x - 4} \right)dx} \). B. \(S = \int\limits_{ - 1}^2 {\left| {2{x^2} - 2x - 4} \right|dx} \) C. \(S = \int\limits_{ - 1}^2 {\left| {\left( {{x^2} - 1} \right) - \left( { - {x^2} + 2x + 3} \right)} \right|dx} \) D. \(S = \int\limits_{ - 1}^2 {\left( { - {x^2} - x + 2} \right)} \). Câu 15. Cho hình (H) giới hạn bởi các đường \(y = \sqrt x ,x = 4\) và trục hoành. Quay hình (H) quanh trục Ox ta được khối tròn xoay có thể tích là bao nhiêu? A. \(\frac{{15\pi }}{2}\) B. \(\frac{{14\pi }}{3}\) C. \(8\pi \) D. \(\frac{{16\pi }}{3}\) Phần 4 Số phức Câu 1. Số phức nào sau đây là số thuần ảo A. \(z = \sqrt 3 + i\) B. \(z = - 2\) C. \(z = - 2 + 3i\) D. \(z = 3i\) Câu 2. Tìm mô đung của số phức \(z = - 4i\) : A. 4 B. - 4 C. \(\sqrt 4 \) D. \({4^2}\) Câu 3. Cho các điểm A, B, C nằm trong mặt phẳng phức lần lượt biểu diễn các số phức \(1 + 3i, - 2 + 2i,1 - 7i\). Gọi D là điểm sao cho tứ giác ABCD là hình bình hành. Điểm D biểu diễn số phức nào trong các số phức sau đây? A. \(z = 4 + 6i\) B. \(z = 2 + 8i\) C. \(z = - 2 - 8i\) D. \(4 - 6i\) Câu 4. Cho hai số phức \({z_1} = 2 + i,{z_2} = 1 + 3i\). Phần thực của số phức \({z_1} + {z_2}\) bằng: A. 1 B. 3 C. 4 D. -2 Câu 5. Tính mô đun của số phức z biết \(\overline z = \left( {4 - 3i} \right)\left( {1 + i} \right)\) A. \(\left| z \right| = 5\sqrt 2 \) B. \(\left| z \right| = \sqrt 2 \) C. \(\left| z \right| = 25\sqrt 2 \) D. \(\left| z \right| = 7\sqrt 2 \) Câu 6. Cho số phức \(z = \frac{{\left( {2 - 3i} \right)\left( {4 - i} \right)}}{{3 + 2i}}\). Tọa độ điểm biểu diễn của số phức z trên mặt phẳng Oxy. A. \(\left( {1;4} \right)\) B. \(\left( { - 1;4} \right)\) C. \(\left( { - 1; - 4} \right)\) D. \(\left( {1; - 4} \right)\) Câu 7. Tìm hai số thực x và y thỏa mãn \(\left( {3x + yi} \right)\left( {4 - 2i} \right) = 5x + 2i\) với i là đơn vị ảo. A. \(x = 2;y = 4\) B. \(x = - 2;y = 0\) C. \(x = 2;y = 0\) D. \(x = - 2;y = 4\) Câu 8. Có bao nhiêu số phức đồng thời thỏa mãn \(\left| z \right| = \sqrt {10} \) đồng thời phần ảo gấp 3 lần phần thực A. 1 B. 2 C. 3 D. 4 Câu 9. Gọi A và B lần lượt là hai điểm biểu diễn của hai số phức \(z = 5 + 3i\) và \(z' = 3 + 5i\). Kết luận nào sau đây là đúng? A. A và B đối xứng nhau qua trục hoành B. A và B đối xứng nhau qua trục tung C. A và B đối xứng nhau qua gốc tọa độ D. A và B đối xứng nhau qua đường thẳng \(y = x\) Câu 10. Cho số phức \(z\) thỏa mãn \(\frac{{5\left( {\overline z + i} \right)}}{{z + 1}} = 2 - i\). Mô đung của số phức \(\omega = 1 + z + {z^2}\) là A. \(4\) B. 9 C. 13 D. \(\sqrt {13} \) A. Câu 11. Cho số phức z thỏa mãn \(\left| {z - 1} \right| = 2\). Biết rằng tập hợp điểm biểu diễn các số phức \({\rm{w}} = \left( {1 + i\sqrt 3 } \right)z + 2\) là một đường tròn. Tính bán kính r của đường tròn đó. A. \(r = 16\) B. \(r = 4\) C. \(r = 25\) D. \(r = 9\) Câu 12. Tập hợp các điểm biểu diễn cho số phức z thỏa mãn \(2\left| {z - i} \right| = \left| {z - \overline z + 2i} \right|\) là A. Một đường thẳng B. Một đường tròn C. Một Parabol D. Một Elip Câu 13. Tìm phần thực, phần ảo của số phức z thỏa mãn \(\left( {\frac{z}{2} - i} \right)\left( {1 - i} \right) = {\left( {1 + i} \right)^{3979}}\)? A. Phần thực là \({2^{1990}}\) và phần ảo là 2 B. Phần thực là \( - {2^{1990}}\) và phần ảo là 2 C. Phần thực là \( - {2^{1989}}\) và phần ảo là 1 D. Phần thực là \({2^{1989}}\) và phần ảo là 1 Câu 14. Phương trình \(\left( {2 + i} \right){z^2} + az + b = 0\left( {a,b \in \mathbb{C}} \right)\) có hai nghiệm là \(3 + i\) và \(1 - 2i\). Khi đó a=? A. \( - 9 - 2i\) B. \(15 + 5i\) C. \(9 + 2i\) D. \(15 - 5i\) Câu 15. Trong mặt phẳng phức Oxy, số phức z thỏa điều kiện nào thì có điểm biểu diễn số phức thuộc phần tô màu như hình vẽ? A. \(1 \le \left| z \right| \le 2\) và phần ảo dương. B. \(1 \le \left| z \right| \le 2\) và phần ảo âm. C. \(1 < \left| z \right| < 2\) và phần ảo dương. D. \(1 < \left| z \right| < 2\) và phần ảo âm. Phần 5 Hệ trục tọa độ Câu 1. Cho vecto \(\overrightarrow {AO} = 3\left( {\overrightarrow i + 4\overrightarrow j } \right) - 2\overrightarrow k + 5\overrightarrow j \). Tọa độ của điểm A là: A. (3;-2;5) B. (-3;-17;2) C. (3;17;-2) D. (3;5;-2) Câu 2. Cho \(\overrightarrow m = \left( {1;0; - 1} \right),\overrightarrow n = \left( {0;1;1} \right)\). Kết luận nào sai? A. \(\overrightarrow m .\overrightarrow n = - 1\) B. \(\left[ {\overrightarrow m ,\overrightarrow n } \right] = \left( {1; - 1;1} \right)\) C. \(\overrightarrow m \) và \(\overrightarrow n \) không cùng phương D. Góc của \(\overrightarrow m \) và \(\overrightarrow n \)là \(60^\circ \) Câu 3. Cho \(\overrightarrow a \) và \(\overrightarrow b \) tạo với nhau một góc \(\frac{{2\pi }}{3}\). Biết \(\left| {\overrightarrow a } \right| = 3,\left| {\overrightarrow b } \right| = 5\) thì \(\left| {\overrightarrow a - \overrightarrow b } \right|\) bằng A. 6 B. 5 C. 4 D. 7 Câu 4. Cho hai vecto \(\overrightarrow a = \left( {1;m; - 1} \right),\overrightarrow b = \left( {2;1;3} \right)\). \(\overrightarrow a \bot \overrightarrow b \) khi: A. \(m = - 1\) B. \(m = 1\) C. \(m = 2\) D. \(m = - 2\) Câu 5. Cho ba vevto \(\overrightarrow a = \left( { - 1;0; - 2} \right)\), \(\overrightarrow b = \left( {1;2;1} \right)\), \(\overrightarrow c = \left( {4;3;m} \right)\). Để ba vecto trên đồng phẳng thì m bằng: A. 14 B. 5 C. -7 D. 7 Câu 6. Cho 3 điểm \(M\left( {2;3; - 1} \right),N\left( { - 1;1;1} \right),P\left( {1;m - 1;2} \right)\). Tìm M để \(\Delta MNP\) vuông tại N. A. 3 B. 2 C. 1 D. 0 Câu 7. Cho điểm \(M\left( {3;1; - 2} \right)\). Điểm N đối xứng với M qua Ox có tọa độ là: A. \(\left( { - 3;1;2} \right)\) B. \(\left( { - 3; - 1; - 2} \right)\) C. \(\left( {3;1;0} \right)\) D. \(\left( {3; - 1;2} \right)\) Câu 8. Cho \(A\left( {4;2;6} \right)\), \(B\left( {10; - 2;4} \right),C\left( {4; - 4;0} \right),D\left( { - 2;0;2} \right)\). Tứ giác ABCD là hình: A. Bình hành B. Vuông C. Chữ nhật D. Thoi Câu 9. Cho \(\overrightarrow a \left( {3;2;1} \right),\overrightarrow b \left( { - 2;0;1} \right)\). Độ dài của \(\overrightarrow a + \overrightarrow b \) bằng A. 1 B. 2 C. 3 D. \(\sqrt 2 \) Câu 10. Cho ba điểm \(A\left( {2; - 1;5} \right)\), \(B\left( {5; - 5;7} \right),M\left( {x;y;1} \right)\). Tìm x, y để A, B, M thẳng hàng? A. x = 4,y = 7 B. x = - 4, y = - 7 C. x = 4, y = - 7 D. x = - 4, y = 7 Câu 11. Cho 3 điểm \(A\left( {2;5; - 1} \right),B\left( {2;2;3} \right),C\left( { - 3;2;3} \right)\). Mệnh đề nào sau đây sai? A. \(\Delta ABC\) đều. B. A, B, C không thẳng hàng C. \(\Delta ABC\) vuông D.\(\Delta ABC\) cân tại B. Câu 12. Cho 4 điểm \(A\left( {1;0;0} \right),B\left( {0;1;0} \right),C\left( {0;0;1} \right),D\left( {1;1;1} \right)\). Mệnh đề nào sai? A. 4 điểm A, B, C, D tạo thàng 1 tứ diện B. \(\Delta ABD\) đều C. \(AB \bot CD\) D. \(\Delta BCD\) vuông. Câu 13. Cho \(A\left( {0;2; - 2} \right),B\left( { - 3;1; - 1} \right)\), \(C\left( {4;3;0} \right)\), \(D\left( {1;2;m} \right)\). Tìm m để A, B, C, D đồng phẳng: A. \( - 5\) B. \( - 1\) C. 1 D. 5 Câu 14. Trong không gian Oxyz, cho \(\overrightarrow u = \left( {1;1; - 2} \right),\overrightarrow v = \left( {1;0;m} \right)\). Tìm m để góc giữa hai vecto \(\overrightarrow u ,\overrightarrow v \) bằng \(45^\circ \) A. m=2 B. \(m = 2 - \sqrt 6 \) C. \(m = 2 + \sqrt 6 \) D. \(m = 2 \pm \sqrt 6 \) Câu 15. Trong không gian Oxyz, cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {1;1; - 6} \right),B\left( {0;0; - 2} \right),\)\(C\left( { - 5;1;2} \right),D'\left( {2;1; - 1} \right)\). Thể tích khối hộp đã cho bằng. A. 42 B. 19 C. 38 D. 12. Phần 6 Phương trình mặt phẳng Câu 1. Vecto nào sau đây là vecto pháp tuyến của mặt phẳng \(\left( P \right):4x - 3y + 1 = 0\). A. \(\left( {4; - 3;0} \right)\) B. \(\left( {4; - 3;1} \right)\) C. \(\left( {4; - 3; - 1} \right)\) D. \(\left( { - 3;4;0} \right)\) Câu 2. Phương trình mặt phẳng (P) chứa điểm \(M\left( { - 1;2;0} \right)\) và có veto pháp tuyến \(\overrightarrow n = \left( {4;0; - 5} \right)\) là: A. \(4x - 5y - 4 = 0\) B. \(4x - 5z - 4 = 0\) C. \(4x - 5y + 4 = 0\) D. \(4x - 5z + 4 = 0\) Câu 3. Mặt phẳng song song với hai đường thẳng \({\Delta _1}:\frac{{x - 2}}{2} = \frac{{y + 1}}{{ - 3}} = \frac{z}{4},\)\({\Delta _2}:\left\{ \begin{array}{l}x = 2 + t\\y = 3 + 2t\\z = 1 - t\end{array} \right.\) có một vecto pháp tuyến là: A. \(\overrightarrow n = \left( { - 5;6; - 7} \right)\) B. \(\overrightarrow n = \left( {5 - ;6;7} \right)\) C. \(\overrightarrow n = \left( { - 5; - 6;7} \right)\) D. \(\overrightarrow n = \left( { - 5;6;7} \right)\) Câu 4. Cho hai điểm \(A\left( { - 2;0;1} \right),B\left( {4;2;5} \right)\). Phương trình mặt phẳng trung trục của AB là: A. \(3x + y + 2z - 10 = 0\) B. \(3x + y + 2z + 10 = 0\) C. \(3x + y - 2z - 10 = 0\) D. \(3x - y + 2z - 10 = 0\) Câu 5. Cho \(\left( Q \right):3x - y - 2z + 1 = 0\), (P) song song với (Q), chứa \(A\left( {0;0;1} \right)\) có phương trình là: A. \(3x - y - 2z + 2 = 0\) B. \(3x - y - 2z - 2 = 0\) C. \(3x - y - 2z + 3 = 0\) D. \(3x - y - 2z + + 5 = 0\) Câu 6. Mặt phẳng (P) song song với Oxy và đi qua \(A\left( {1; - 2;1} \right)\) có phương trình là A.\(z - 1 = 0\) B. \(x - 2y + z = 0\) C. \(x - 1 = 0\) D. \(y + 2 = 0\) Câu 7. Cho hai mặt phẳng \(\left( \alpha \right):3x - 2y + 2z + 7 = 0\) và \(\left( \beta \right):5x - 4y + 3z + 1 = 0\). Phương trình mặt phẳng đi qua gốc tọa độ O và vuông góc cả \(\left( \alpha \right),\left( \beta \right)\) là A. \(2x - y + 2z = 0\) B. \(2x + y - 2z = 0\) C. \(2x + y - 2z + 1 = 0\) D. \(2x - y - 2z = 0\) Câu 8. Trong không gian Oxyz, phương trình mặt phẳng (Oxy) là A. \(z = 0\) B. \(x + y = 0\) C. \(x = 0\) D. \(y = 0\) Câu 9. Mặt phẳng (P) chứa \(A\left( {1; - 2;3} \right)\), vuông góc với \(\left( d \right):\frac{{x + 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 1}}{3}\) có phương trình là: A. \(2x - y + 3z - 13 = 0\) B. \(2x - y + 3z + 13 = 0\) C. \(2x - y - 3z - 13 = 0\) D. \(2x + y + 3z - 13 = 0\) Câu 10. Mặt phẳng đi qua \(D\left( {2;0;0} \right)\) vuông góc với trục Oy có phương trình là: A.\(z = 0\). B. \(y = 2\) C. \(y = 0\) D. \(z = 2\) Câu 11. Cho 2 điểm \(A\left( { - 1;0;0} \right),B\left( {0;0;1} \right)\). Mặt phẳng (P) chứa đường thẳng AB và song song với trục O có phương trình là A.\(x - z + 1 = 0\) B. \(x - z - 1 = 0\) C. \(x + y - z + 1 = 0\) D. \(y - z + 1 = 0\) Câu 12. Mặt phẳng (P) chứa Oz và đi qua \(A\left( {1;2;3} \right)\) có phương trình là: A. \(2x - y = 0\) B. \(x + y - z = 0\) C. \(x - y + 1 = 0\) D. \(x - 2y + z = 0\) Câu 13. Trong không gian Oxyz cho mặt phẳng \(\left( Q \right):3x + 4y - 1 = 0\). Mặt phẳng (P) song song với (Q) và cách gốc tọa độ một khoảng bằng 1 có phương trình là: A. \(3x + 4y + 5 = 0\) hoặc \(3x + 4y - 5 = 0\) B. \(3x + 4y + 5 = 0\) C. \(3x + 3y - 5 = 0\) D. \(4x + 3y + 5 = 0\) hoặc \(3x + 4y + 5 = 0\) Câu 14. Mặt phẳng (P) đi qua \(M\left( {1;2;2} \right)\) và cắt trục Ox, Oy, Oz lần lượt tại A, B, C sao cho M là trực tâm của tam giác ABC. Phương trình của (P) là: A. \(2x + y + z - 4 = 0\) B. \(2x + y + z - 2 = 0\) C. \(2x + 4y + 4z - 9 = 0\) D. \(x + 2y + 2z - 9 = 0\) Câu 15. Viết phương trình mặt phẳng (P) biết (P) cắt ba trục tọa độ lần lượt tại A, B, C sao cho \(M\left( {1;2;3} \right)\) làm trọng tâm tam giác ABC: A. \(6x + 3y + 2z - 18 = 0\) B. \(x + 2y + 3z = 0\) C. \(6x - 3y + 2z - 18 = 0\) D. \(6x + 3y + 2z + 18 = 0\) Phần 7 Phương trình đường thẳng Câu 1. Cho đường thẳng d đi qua \(M\left( {2;0; - 1} \right)\) và có vecto chỉ phương \(\overrightarrow a \left( {4; - 6;2} \right)\). Phương trình tham số của đường thẳng d là: A. \(\left\{ \begin{array}{l}x = - 2 + 2t\\y = - 3t\\z = 1 + t\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 3t\\z = - 1 + t\end{array} \right.\) C. \(\left\{ \begin{array}{l}x = 4 + 2t\\y = - 6 - 3t\\z = 2 + t\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = - 2 + 4t\\y = - 6t\\z = 1 + 2t\end{array} \right.\) Câu 2. Phương trình đường thẳng AB với \(A\left( {1;1;2} \right),B\left( {2; - 1;0} \right)\) là: A. \(\frac{{x - 1}}{3} = \frac{{y - 1}}{2} = \frac{{z - 2}}{2}\) B. \(\frac{{x + 1}}{{ - 1}} = \frac{{y + 1}}{2} = \frac{{z + 2}}{2}\) C. \(\frac{{x - 2}}{3} = \frac{{y + 1}}{{ - 2}} = \frac{z}{3}\) D. \(\frac{x}{1} = \frac{{y - 3}}{{ - 2}} = \frac{{z - 4}}{{ - 2}}\) Câu 3. Cho đường thẳng d đi qua điểm \(A\left( {1;2;3} \right)\) và vuông góc với mặt phẳng \(\left( \alpha \right):4x + 3y - 7z + 1 = 0\). Phương trình tham số của d là: A. \(\left\{ \begin{array}{l}x = 1 + 4t\\y = 2 + 3t\\z = 3 - 7t\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = - 1 + 8t\\y = - 2 + 6t\\z = - 3 - 14t\end{array} \right.\) C. \(\left\{ \begin{array}{l}x = 1 + 3t\\y = 2 - 4t\\z = 3 - 7t\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = - 1 + 4t\\y = - 2 + 3t\\z = - 3 - 7t\end{array} \right.\) Câu 4. Cho \(A\left( {0;0;1} \right),B\left( { - 1; - 2;0} \right),C\left( {2;1; - 1} \right)\). Đường thẳng \(\Delta \) đi qua trọng tâm G của tam giác ABC và vuông góc với mặt phẳng \(\left( {ABC} \right)\) có phương trình. A. \(\left\{ \begin{array}{l}x = \frac{1}{3} + 5t\\y = - \frac{1}{3} + 4t\\z = 3t\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = \frac{1}{3} + 5t\\y = - \frac{1}{3} - 4t\\z = 3t\end{array} \right.\) C. \(\left\{ \begin{array}{l}x = \frac{1}{3} - 5t\\y = - \frac{1}{3} - 4t\\z = - 3t\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = \frac{1}{3} - 5t\\y = - \frac{1}{3} - 4t\\z = 3t\end{array} \right.\) Câu 5. Cho hai mặt phẳng \(\left( P \right):2x + y - z - 3 = 0\)và \(\left( Q \right):x + y + z - 1 = 0\). Phương trình chính tắc của đường thẳng giao tuyến của 2 mặt phẳng (P) và (Q) là: A. \(\frac{x}{2} = \frac{{y - 2}}{{ - 3}} = \frac{{z + 1}}{1}\) B. \(\frac{{x + 1}}{{ - 2}} = \frac{{y - 2}}{{ - 3}} = \frac{{z - 1}}{1}\) C. \(\frac{{x - 1}}{2} = \frac{{y + 2}}{3} = \frac{{z + 1}}{1}\) D. \(\frac{x}{2} = \frac{{y + 2}}{{ - 3}} = \frac{{z - 1}}{{ - 1}}\) Câu 6. Trong không gian Oxyz, cho tam giác ABC với \(A\left( {1; - 3;4} \right),B\left( { - 2; - 5; - 7} \right)\) và \(C\left( {6; - 3; - 1} \right)\). Phương trình đường trung tuyến AM của tam giác ABC là: A. \(\frac{{x - 1}}{3} = \frac{{y + 3}}{4} = \frac{{z - 4}}{{ - 1}}\) B. \(\frac{{x - 1}}{3} = \frac{{y + 3}}{{ - 2}} = \frac{{z - 4}}{{ - 11}}\) C. \(\frac{{x - 1}}{1} = \frac{{y + 1}}{{ - 3}} = \frac{{z + 8}}{{ - 4}}\) D. \(\frac{{x - 1}}{1} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 4}}{{ - 8}}\) Câu 7. Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng có phương trình \(d:\frac{{x - 2}}{1} = \frac{{y - 1}}{1} = \frac{{z - 1}}{{ - 1}}\) và mặt phẳng \(\left( P \right):x + my + \left( {{m^2} - 1} \right)z - 7 = 0\). Tìm m để đường thẳng d song song với (P). A. \(m = - 1\) B. \(m = 1\) hoặc \(m = - 2\) C. \(m = - 2\) D. \(m = 2\) hoặc \(m = - 1\) Câu 8. Trong không gian Oxyz, cho hai đường thẳng \(\left( {{\Delta _1}} \right):\left\{ \begin{array}{l}x = - 3 + 2t\\y = 1 - t\\z = - 1 + 4t\end{array} \right.\) và \(\left( {{\Delta _2}} \right):\frac{{x + 4}}{3} = \frac{{y + 2}}{2} = \frac{{z - 4}}{{ - 1}}\). Khẳng định nào sau đây đúng? A. \(\left( {{\Delta _1}} \right)//\left( {{\Delta _2}} \right)\) B. \(\left( {{\Delta _1}} \right)\) và \(\left( {{\Delta _2}} \right)\) chéo và vuông góc với nhau C. \(\left( {{\Delta _1}} \right)\) cắt và không vuông góc với \(\left( {{\Delta _2}} \right)\) D. \(\left( {{\Delta _1}} \right)\) cắt và vuông góc với \(\left( {{\Delta _2}} \right)\) Câu 9. Trong không gian Oxyz, cho điểm \(M\left( {1; - 3;4} \right)\), đường thẳng \(d:\frac{{x + 2}}{3} = \frac{{y - 5}}{{ - 5}} = \frac{{z - 2}}{{ - 1}}\) và mặt phẳng \(\left( P \right):2x + z - 2 = 0\). Viết phương trình đường thẳng \(\Delta \) qua M vuông góc với d và song song với (P). A. \(\Delta :\frac{{x - 1}}{1} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 4}}{{ - 2}}\) B. \(\Delta :\frac{{x - 1}}{1} = \frac{{y + 3}}{1} = \frac{{z - 4}}{{ - 2}}\) C. \(\Delta :\frac{{x - 1}}{{ - 1}} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 4}}{{ - 2}}\) D. \(\Delta :\frac{{x - 1}}{1} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 4}}{2}\) Câu 10. Trong không gian Oxyz, cho đường thẳng \(\Delta \) là giao tuyến của hai mặt phẳng \(\left( P \right):z - 1 = 0\) và \(\left( Q \right):x + y + z - 3 = 0\). Gọi d là đường thẳng nằm trong mặt phẳng (P), cắt đường thẳng \(\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 3}}{{ - 1}}\) và vuông góc với đường thẳng \(\Delta \). Phương trình của đường thẳng d là: A. \(\left\{ \begin{array}{l}x = 3 + t\\y = t\\z = 1 + t\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = 3 - t\\y = t\\z = 1\end{array} \right.\) C. \(\left\{ \begin{array}{l}x = 3 + t\\y = t\\z = 1\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = 3 + t\\y = - t\\z = 1 + t\end{array} \right.\) Phần 8 Phương trình mặt cầu Câu 1. Phương trình nào sau đây là phương trình mặt cầu ? A.\({x^2} + {y^2} + {z^2} - 2x = 0.\) B. \({x^2} + {y^2} - {z^2} + 2x - y + 1 = 0.\) C. \(2{x^2} + 2{y^2} = {\left( {x + y} \right)^2} - {z^2} + 2x - 1.\) D. \({\left( {x + y} \right)^2} = 2xy - {z^2} - 1.\) Câu 2. Phương trình nào sau đây không phải là phương trình mặt cầu ? A. \({x^2} + {y^2} + {z^2} - 2x = 0.\) B. \(2{x^2} + 2{y^2} = {\left( {x + y} \right)^2} - {z^2} + 2x - 1.\) C. \({x^2} + {y^2} + {z^2} + 2x - 2y + 1 = 0.\) D. \({\left( {x + y} \right)^2} = 2xy - {z^2} + 1 - 4x.\) Câu 3. Phương trình nào sau đây không phải là phương trình mặt cầu ? A. \({\left( {x - 1} \right)^2} + {\left( {2y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 6.\) B. \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 6.\) C. \({\left( {2x - 1} \right)^2} + {\left( {2y - 1} \right)^2} + {\left( {2z + 1} \right)^2} = 6.\) D. \({\left( {x + y} \right)^2} = 2xy - {z^2} + 3 - 6x.\) Câu 4. Cho các phương trình sau: \({\left( {x - 1} \right)^2} + {y^2} + {z^2} = 1;\) \({x^2} + {\left( {2y - 1} \right)^2} + {z^2} = 4;\) \({x^2} + {y^2} + {z^2} + 1 = 0;\) \({\left( {2x + 1} \right)^2} + {\left( {2y - 1} \right)^2} + 4{z^2} = 16.\) Số phương trình là phương trình mặt cầu là: A. 4. B. 3. C. 2. D. 1. Câu 5. Mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {z^2} = 9\) có tâm là: A. \(I\left( {1; - 2;0} \right).\) B. \(I\left( { - 1;2;0} \right).\) C. \(I\left( {1;2;0} \right).\) D. \(I\left( { - 1; - 2;0} \right).\) Câu 6. Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 8x + 2y + 1 = 0\) có tâm là: A. \(I\left( {8; - 2;0} \right).\) B. \(I\left( { - 4;1;0} \right).\) C. \(I\left( { - 8;2;0} \right).\) D. \(I\left( {4; - 1;0} \right).\) Câu 7. Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 4x + 1 = 0\) có tọa độ tâm và bán kính R là: A. \(I\left( {2;0;0} \right),{\rm{ }}R = \sqrt 3 .\) B. \(I\left( {2;0;0} \right),{\rm{ }}R = 3.\) C. \(I\left( {0;2;0} \right),{\rm{ }}R = \sqrt 3 .\) D. \(I\left( { - 2;0;0} \right),{\rm{ }}R = \sqrt 3 .\) Câu 8. Phương trình mặt cầu có tâm \(I\left( { - 1;2; - 3} \right)\), bán kính \(R = 3\) là: A. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 9.\) B. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^2} = 3.\) C. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^2} = 9.\) D. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^2} = 9.\) Câu 9. Mặt cầu \(\left( S \right):{\left( {x + y} \right)^2} = 2xy - {z^2} + 1 - 4x\) có tâm là: A. \(I\left( { - 2;0;0} \right).\) B. \(I\left( {4;0;0} \right).\) C. \(I\left( { - 4;0;0} \right).\) D. \(I\left( {2;0;0} \right).\) Câu 10. Đường kính của mặt cầu \(\left( S \right):{x^2} + {y^2} + {\left( {z - 1} \right)^2} = 4\) bằng: A. 4. B. 2. C. 8. D. 16. Câu 11. Cho đường thẳng \(d:\left\{ \begin{array}{l}x = t\\y = - 1 + 3t\\z = 1\end{array} \right.\). Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của đường thẳng d và trục Ox là: A.\({\left( {x - 1} \right)^2} + {y^2} + {\left( {z - 2} \right)^2} = \frac{1}{2}.\) B.\({\left( {x + 1} \right)^2} + {y^2} + {\left( {z + 2} \right)^2} = \frac{1}{4}.\) C. \({\left( {x - 1} \right)^2} + {y^2} + {z^2} = \frac{1}{2}.\) D. \({\left( {x - \frac{1}{3}} \right)^2} + {y^2} + {\left( {z - \frac{1}{2}} \right)^2} = \frac{1}{4}.\) Câu 12. Cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 2t\\y = t\\z = 4\end{array} \right.\)và \(d':\left\{ \begin{array}{l}x = {t^'}\\y = 3 - t'\\z = 0\end{array} \right.\). Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của đường thẳng d và d’ là: A. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 4.\) B. \({\left( {x - 2} \right)^2} + {y^2} + {z^2} = 4.\) C. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 2.\) D.\({\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 4.\) Câu 13. Cho các điểm \(A\left( { - 2;4;1} \right)\) và \(B\left( {2;0;3} \right)\) và đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{{ - 2}}\). Gọi \(\left( S \right)\) là mặt cầu đi qua A, B và có tâm thuộc đường thẳng D. Bán kính mặt cầu (S) bằng: A. \(\frac{{\sqrt {1169} }}{4}.\)B.\(\frac{{\sqrt {873} }}{4}.\)C. \(\frac{{1169}}{{16}}.\)D.\(\frac{{\sqrt {967} }}{2}.\) Câu 14. Phương trình mặt cầu có tâm \(I\left( { - \sqrt 6 ; - \sqrt 3 ;\sqrt 2 - 1} \right)\) và tiếp xúc trục Oz là: A.\({\left( {x + \sqrt 6 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {\left( {z - \sqrt 2 + 1} \right)^2} = 9.\) B.\({\left( {x + \sqrt 6 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {\left( {z - \sqrt 2 - 1} \right)^2} = 9.\) C. \({\left( {x + \sqrt 6 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {\left( {z - \sqrt 2 - 1} \right)^2} = 3.\) D. \({\left( {x + \sqrt 6 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {\left( {z - \sqrt 2 + 1} \right)^2} = 3.\) Câu 15. Phương trình mặt cầu có tâm \(I\left( {4;6; - 1} \right)\) và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB vuông là: A.\({\left( {x - 4} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 1} \right)^2} = 26.\) B. \({\left( {x - 4} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 1} \right)^2} = 74.\) C. \({\left( {x - 4} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 1} \right)^2} = 34.\) D.\({\left( {x - 4} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 1} \right)^2} = 104.\) Câu 16. Phương trình mặt cầu có tâm \(I\left( {\sqrt 3 ; - \sqrt 3 ;0} \right)\) và cắt trục Oz tại hai điểm A, B sao cho tam giác IAB đều là: A.\({\left( {x + \sqrt 3 } \right)^2} + {\left( {y - \sqrt 3 } \right)^2} + {z^2} = 8.\) B.\({\left( {x - \sqrt 3 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {z^2} = 9.\) C. \({\left( {x + \sqrt 3 } \right)^2} + {\left( {y - \sqrt 3 } \right)^2} + {z^2} = 9.\) D. \({\left( {x - \sqrt 3 } \right)^2} + {\left( {y + \sqrt 3 } \right)^2} + {z^2} = 8.\) Câu 17. Phương trình mặt cầu có tâm \(I\left( {3;6; - 4} \right)\) và cắt trục Oz tại hai điểm A, B sao cho diện tích tam giác IAB bằng \(6\sqrt 5 \) là: A. \({\left( {x - 3} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 4} \right)^2} = 49.\) B.\({\left( {x - 3} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 4} \right)^2} = 45.\) C. \({\left( {x - 3} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 4} \right)^2} = 36.\) D.\({\left( {x - 3} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z + 4} \right)^2} = 54.\) Câu 18. Mặt cầu (S) có tâm \(I\left( {2;1; - 1} \right)\) và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB vuông. Điểm nào sau đây thuộc mặt cầu (S): A. \(\left( {2;1;1} \right).\) B. \(\left( {2;1;0} \right).\) C. \(\left( {2;0;0} \right).\) D. \(\left( {1;0;0} \right).\) Câu 19. Gọi (S) là mặt cầu có tâm \(I\left( {1; - 3;0} \right)\) và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB đều. Điểm nào sau đây không thuộc mặt cầu (S): A. \(\left( { - 1; - 3;2\sqrt 3 } \right).\) B. \(\left( {3; - 3;2\sqrt 2 } \right).\) C. \(\left( {3; - 3; - 2\sqrt 2 } \right).\) D. \(\left( {2; - 1;1} \right).\) Câu 20. Cho các điểm \(I\left( { - 1;0;0} \right)\) và đường thẳng \(d:\frac{{x - 2}}{1} = \frac{{y - 1}}{2} = \frac{{z - 1}}{1}\). Phương trình mặt cầu \(\left( S \right)\) có tâm I và tiếp xúc d là: A. \({\left( {x + 1} \right)^2} + {y^2} + {z^2} = 5.\) B.\({\left( {x - 1} \right)^2} + {y^2} + {z^2} = 5.\) C. \({\left( {x + 1} \right)^2} + {y^2} + {z^2} = 10.\) D.\({\left( {x - 1} \right)^2} + {y^2} + {z^2} = 10.\) HocTot.XYZ
|