Đề cương ôn thi học kì I môn toán lớp 10 (bài tập)Tổng hợp các câu hỏi có khả năng xuất hiện trong đề thi HK1 Toán học 10 sắp tới
Lựa chọn câu để xem lời giải nhanh hơn
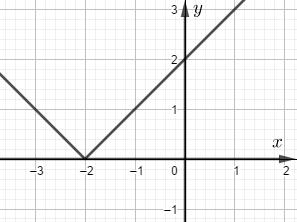
PHẦN 1 Mệnh đề- Tập hợp Bài 1: Các mệnh đề sau đúng hay sai? a) 2 là số chẵn b) 2 là số nguyên tố c) 2 là số chính phương Giải: Mệnh đề đúng là a và b Mệnh đề sai là c Bài 2: Tìm \(x \in D\) để \(P(x)\) đúng trong các trường hợp sau: a) \(P(x)\): “\(2x + 3 \le 0\)” b) \(P(x)\): “\({\left( {2x + 3} \right)^2} \le 0\)” Giải: a) \(2x + 3 \le 0 \Leftrightarrow x \le - \dfrac{3}{2}\)\( \Rightarrow D = \left( { - \infty ; - \dfrac{3}{2}} \right]\) b) \({\left( {2x + 3} \right)^2} \le 0 \Leftrightarrow 2x + 3 = 0\\ \Leftrightarrow x = - \dfrac{3}{2} \)\(\Rightarrow D = \left\{ { - \dfrac{3}{2}} \right\}\) Bài 3: Sử dụng thuật ngữ “điều kiện cần”, “điều kiện đủ” để phát biểu định lí: a) Tứ giác ABCD là hình vuông khi và chỉ khi tứ giác đó là hình thoi có một góc vuông. b) Một số chia hết cho 6 khi và chỉ khi nó chia hết cho 2 và cho 3. c) Nếu số tự nhiên \(n\) chia hết cho 2 thì \({n^2}\) chia hết cho 4. Giải: a) Tứ giác ABCD là hình vuông là điều kiện cần và đủ để ABCD là hình thoi có một góc vuông. b) Số chia hết cho 6 là điều kiện cần và đủ để số đó chia hết cho 2 và cho 3. c) \(n\) chia hết cho 2 là điều kiện đủ để \({n^2}\) chia hết cho 4. \({n^2}\) chia hết cho 4 là điều kiện cần để \(n\) chia hết cho 2. Bài 4: Chứng minh định lí “ Nếu n là số tự nhiên chẵn thì \({n^2}\) chia hết cho 4” Giải: Vì n chẵn nên \(n = k(k \in \mathbb{N})\). Khi đó \({n^2} = 4{k^2}\) chia hết cho 4 nên \({n^2}\) chia hết cho 4. Bài 5: Chứng minh đinh lí “ Với mọi số tự nhiên n nếu 3n+2 là số lẻ thì n là số lẻ” Giải: Giả sử n là số chẵn khi đó \(n = 2k(k \in \mathbb{N})\) \( \Rightarrow 3n + 2 = 3.2k + 2 = 2\left( {3k + 1} \right)\) chia hết cho 2 nên 3n+2 là số chẵn trái với dữ kiện bài cho. Vậy n lẻ. Bài 6. Tìm tập hợp các nghiệm thực của phương trình \(x\left( {{x^2} - 4} \right)\left( {x + 1} \right)\left( {x + 3} \right) = 0\) Giải: Cách 1: \(A = \left\{ { - 3; - 2; - 1;0;2} \right\}\) Cách 2: \(A = \left\{ {x \in \mathbb{R}|x\left( {{x^2} - 4} \right)\left( {x + 1} \right)\left( {x + 3} \right) = 0} \right\}\) Bài 7. Tìm tất cả các tập hợp con của tập hợp sau \(A = \left\{ {0;3;5} \right\}\) Giải: Tập con của A là: \(\emptyset ;\left\{ 0 \right\};\left\{ 3 \right\};\left\{ 5 \right\};\left\{ {0;3} \right\};\left\{ {3;5} \right\};\left\{ {0;5} \right\};A\) Bài 8: Hai tập hợp \(A = \left\{ {x \in \mathbb{R}| - 2 \le x \le 2} \right\}\) và \(B = \left\{ {x \in \mathbb{R}|{x^2} - x - 6 < 0} \right\}\) có bằng nhau không? Giải: Ta có:\(B = \left\{ {x \in \mathbb{R}| - 2 < x < 3} \right\}\) Vì \( - 2 \in A\) mà \( - 2 \notin B\) nên \(A \not\subset B\)\( \Rightarrow A \ne B\) Bài 9: Cho hai tập hợp \(A = \left\{ {x \in \mathbb{R}|x\left( {{x^2} - x - 6} \right) = 0} \right\}\) và \(B = \left\{ {x \in \mathbb{R}|{x^4} - 13{x^2} + 36 = 0} \right\}\). Tìm \(A \cap B;A \cup B;A\backslash B;B\backslash A\) Giải: \(A = \left\{ { - 2;0;3} \right\}\);\(B = \left\{ { - 3; - 2;2;3} \right\}\) \(A \cap B = \left\{ { - 2;3} \right\}\);\(A \cup B = \left\{ { - 3; - 2;0;2;3} \right\}\);\(A\backslash B = \left\{ 0 \right\}\);\(B\backslash A = \left\{ {2; - 3} \right\}\). PHẦN 2 Hàm số bậc nhất và bậc hai Bài 1. Tìm tập xác định của hàm số a) \(y = \dfrac{{x - 2}}{{\sqrt {x + 6} }}\) \(D = \left( { - 6; + \infty } \right)\) b) \(y = \dfrac{3}{{x - 1}}\) \(D = \mathbb{R}\backslash \left\{ 1 \right\}\) c) \(y = \sqrt {x - 5} + {x^2} + 1\) \(D = \left[ {5; + \infty } \right)\) d) \(y = \dfrac{{\sqrt {x + 2} }}{{{x^2} + 4x + 3}}\) \(D = \left[ { - 2; - 1} \right) \cup \left( { - 1; + \infty } \right)\) Bài 2: Xét tính chẵn- lẻ hàm số \(y = \left| {x + 2} \right|\). Giải: TXĐ: \(D = \mathbb{R}\) Ta có \( - x \in D\forall x \in D\) và \(f\left( { - x} \right) = \left| {\left( { - x} \right) + 2} \right|\\ = \left| { - x + 2} \right| \ne \pm \left| {x + 2} \right|\)\( \Rightarrow \) Hàm số không chẵn không lẻ. Bài 3. Cho hàm số \(y = x + 2\). a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số trên. b) Tịnh tiến đồ thị trên sang phải 3 đơn vị rồi xuống dưới 1 đơn vị ta được đồ thị của hàm số nào? c) Vẽ đồ thị hàm số \(y = \left| {x + 2} \right|\). Giải: a) a=1 nên hàm số đồng biến trên \(\mathbb{R}\). Đồ thị của hàm số là một đường thẳng qua 2 điểm \(A\left( {0;2} \right),B\left( { - 2;0} \right)\).
b) Tịnh tiến đồ thị sang phải 3 đơn vị ta được đồ thị của hàm số \(y = \left( {x - 3} \right) + 2 = x - 1\). Tịnh tiến đồ thị này xuống dưới 1 đơn vị ta được đồ thị của hàm số \(y = x - 1 - 1 = x - 2\). c) Ta có \(y = \left| {x + 2} \right| = \left\{ \begin{array}{l}x + 2{\rm{ khi }}x \ge - 2\\ - x - 2{\rm{ khi }}x < - 2\end{array} \right.\) Vẽ đồ thị hàm số \(y = \left\{ \begin{array}{l}x + 2{\rm{ khi }}x \ge - 2\\ - x - 2{\rm{ khi }}x < - 2\end{array} \right.\) ta được:
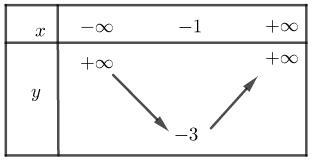
Bài 4. Tìm m để hàm số \(y = \left( {m - 2} \right)x + 5\): a) Có đồ thị vuông góc với đường thẳng \(x + 2y + 1 = 0\) b) Có đồ thị cắt đường thẳng \(y = x + 3\) tại điểm có tung độ bằng \(2\). c) Đồng biến trên \(\mathbb{R}\) với m nguyên thuộc đoạn \(\left[ {1;5} \right]\). d) Đồ thị hàm số cắt 2 trục Ox, Oy tại M, N sao cho tam giác OMN cân. e) \(y > 0\forall x \in \left[ {0;2} \right]\) Đáp án a) \(x + 2y + 1 = 0 \Leftrightarrow y = - \dfrac{1}{2}x - \dfrac{1}{2}\) Đồ thị hàm số \(y = \left( {m - 2} \right)x + 5\) vuông góc với đường thẳng \(y = - \dfrac{1}{2}x - \dfrac{1}{2}\) \( \Leftrightarrow \left( {m - 1} \right).\left( { - \dfrac{1}{2}} \right) = - 1 \\\Leftrightarrow m - 1 = 2 \Leftrightarrow m = 3\) b) Thay \(y = 2\) vào phương trình đường thẳng \(y = x + 3\) ta được \(x = - 1\). Đường thẳng \(y = \left( {m - 2} \right)x + 5\) cắt đường thẳng \(y = x + 3\) tại điểm có tung độ bằng 2 khi và chỉ khi \(A\left( { - 1;2} \right)\) thuộc đường thẳng \(y = \left( {m - 2} \right)x + 5\)\( \Leftrightarrow \left( {m - 2} \right)\left( { - 1} \right) + 5 = 2 \Leftrightarrow m = 5\). c) Hàm số đồng biến trên \(\mathbb{R}\) khi và chỉ khi \(m - 2 > 0 \Leftrightarrow m > 2\). Do m nguyên thuộc đoạn \(\left[ {1;5} \right]\) nên \(m \in \left\{ {2;3;4;5} \right\}\). d) Đồ thị cắt 2 trục tọa độ Ox, Oy lần lượt tại M, N. Nên \(M\left( {\dfrac{5}{{2 - m}};0} \right);N\left( {0;5} \right)\). Tam giác OMN cân \(\begin{array}{l} \Leftrightarrow OM = ON \Leftrightarrow \dfrac{5}{{\left| {m - 2} \right|}} = 5\\\Leftrightarrow \left| {m - 2} \right| = 1\\ \Leftrightarrow \left[ \begin{array}{l}m - 2 = 1\\m - 2 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = 1\end{array} \right.\end{array}\) e) \(y > 0\forall x \in \left[ {0;2} \right] \Leftrightarrow \left( {m - 2} \right)x + 5 > 0\)\(\forall x \in \left[ {0;2} \right]\)(1) TH1: \(m - 2 \ge 0 \Leftrightarrow m \ge 2\) \( \Rightarrow \left( {m - 2} \right)x + 5 \ge 0 + 5 = 5 > 0\)\(\forall x \in \left[ {0;2} \right]\) TH2: \(m - 2 < 0 \Leftrightarrow m < 2\) \(\begin{array}{l}(1) \Leftrightarrow x < - \dfrac{5}{{m - 2}}\forall x \in \left[ {0;2} \right]\\ \Leftrightarrow 2 < - \dfrac{5}{{m - 2}} \Leftrightarrow \dfrac{{2m + 1}}{{m - 2}} < 0\\ \Leftrightarrow - \dfrac{1}{2} < m < 2\end{array}\) Vậy \(m > - \dfrac{1}{2}\) thì \(y > 0\) Bài 5. Cho của hàm số \(y = {x^2} + 2x - 2\) có đồ thị là một parabol (P) . a) Lập bảng biến thiên và vẽ đồ thị của hàm số trên. b) Tìm giao điểm của (P) và đường thẳng d: \(y = x + 4\). c) Tìm m để đường thẳng \(y = \dfrac{m}{2}\) cắt đồ thị tại 2 điểm phân biệt có hoành độ âm. Giải: a) (P) có đỉnh \(I\left( { - 1; - 3} \right)\), trục đối xứng\(x = - 1\). Do \(a = 1 > 0\) nên hàm số đồng biến trên \(\left( { - 1; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - 1} \right)\). Bảng biến thiên:
Đồ thị hàm số đi qua điểm \(A\left( {1;1} \right);B\left( {0; - 2} \right);C\left( {2;6} \right)\).
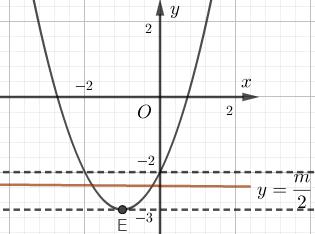
b) Hoành độ giao điểm của (P) và đường thẳng \(y = x + 3\) là nghiệm của phương trình \({x^2} + 2x - 2 = x + 4\) \( \Leftrightarrow {x^2} + x - 6 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 2\end{array} \right.\) Giao điểm của (P) và đường thẳng \(y = x + 3\) là \(M\left( { - 3; - 1} \right);C\left( {2;6} \right)\). c) Đường thẳng \(y = \dfrac{m}{2}\) là đường thẳng song song hoặc trùng với trục Ox.
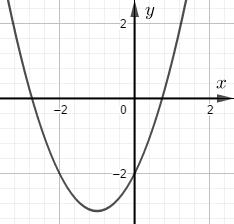
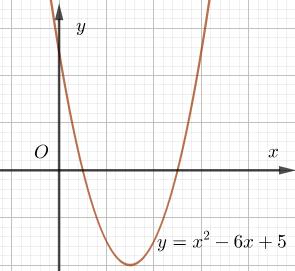
Từ đồ thị ta thấy (P) giao với đường thẳng này tại 2 điểm có hoành độ âm khi và chỉ khi 2 điểm đó nằm bên trái trục Oy. Hay \( - 3 < \dfrac{m}{2} < - 2 \Leftrightarrow - 6 < m < - 4\). Bài 6 a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = {x^2} - 6x + 5(P)\). b) Từ đồ thị (P) suy ra đồ thị \(\left( {{P_1}} \right),\left( {{P_2}} \right)\): \(({P_1}):y = \left| {{x^2} - 6x + 5} \right|\) \(\left( {{P_2}} \right):y = {x^2} - 6\left| x \right| + 5\) c) Từ đồ thị biện luận theo m số nghiệm của phương trình: 1)\(\left| {{x^2} - 6x + 5} \right| = m + 1\) 2) \({x^2} - 6\left| x \right| + 5 = m - 1\) d) Tìm m để phương trình \({x^2} - 6x + m - 2 = 0\) có 2 nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(1 < {x_1} < {x_2} < 5\) Giải a) Đồ thị hàm số \(y = {x^2} - 6x + 5\) có đỉnh \(I\left( {3; - 4} \right)\), nhận trục x=3 làm trục đối xứng và đi qua các điểm \(A\left( {0;5} \right);B\left( {5;0} \right);C\left( {1;0} \right)\).
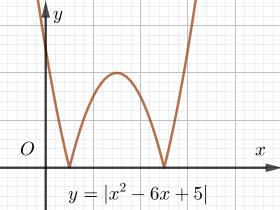
b) Từ đồ thị (P) ta lấy đối xứng qua trục hoành rồi bỏ đi phần đồ thị có tung độ âm thì ta được đồ thị \(\left( {{P_1}} \right)\).
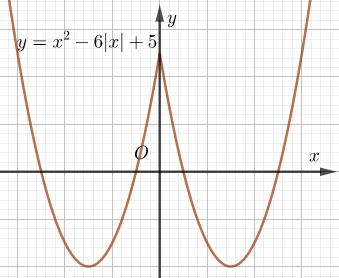
Từ đồ thị (P) ta bỏ đi phần đồ thị có hoành độ âm rồi lấy đối xứng qua trục tung ta được đồ thị của \(\left( {{P_2}} \right)\).
c) 1) Hoành độ giao điểm của \(\left( {{P_1}} \right)\) và đường thẳng \(y = m + 1\) là nghiệm của phương trình \(\left| {{x^2} - 6x + 5} \right| = m + 1\) nên số nghiệm của phương trình \(\left| {{x^2} - 6x + 5} \right| = m + 1\) bằng số giao điểm của đường thẳng \(y = m + 1\) và \(\left( {{P_1}} \right)\). 2) Hoành độ giao điểm của \(\left( {{P_2}} \right)\) và đường thẳng \(y = m - 1\) là nghiệm của phương trình \({x^2} - 6\left| x \right| + 5 = m - 1\) nên số nghiệm của phương trình \({x^2} - 6\left| x \right| + 5 = m - 1\) bằng số giao điểm của đường thẳng \(y = m - 1\) và \(\left( {{P_2}} \right)\) d) Ta có \({x^2} - 6x + m - 2 = 0 \)\(\Leftrightarrow {x^2} - 6x + 5 = 7 - m\). Nghiệm của phương trình là hoành độ giao điểm của đồ thị (P) và đường thẳng \(y = 7 - m\). Ta có: Với \(x = 1 \Rightarrow y = 0\) Với \(x = 5 \Rightarrow y = 0\) Từ đồ thị ta có đường thẳng \(y = 7 - m\) cắt (P) tại 2 điểm có hoành độ thỏa mãn \(1 < {x_1} < {x_2} < 5\) khi và chỉ khi \( - 3 < 7 - m < 0\)\( \Leftrightarrow 7 < m < 10\). Bài 7: Cho parabol (P): \(y = {x^2} + \left( {a + 1} \right)x - 2b\). Xác định a, b biết (P) cắt trục tung tại điểm có tung độ \(y = 1\) và nhận đường thẳng \(x = - 2\) làm trục đối xứng. Giải: (P) cắt trục tung tại điểm có tung độ \(y = 1\) nên ta có: \(1 = {0^2} + \left( {a + 1} \right).0 - 2b \Leftrightarrow b = - \dfrac{1}{2}\) (P) nhận đường thẳng \(x = - 2\) làm trục đối xứng nên \( - \dfrac{{a + 1}}{2} = - 2 \Leftrightarrow a = 3\) Vậy \(a = 3;b = - \dfrac{1}{2}\). Bài 8: a) Tìm m để giá trị nhỏ nhất của hàm số \(y = 4{x^2} - 4mx + {m^2} - m\) trên \(\mathbb{R}\) bằng 2 b) Tìm m để giá trị lớn nhất của hàm số \(y = - 2{x^2} + 3mx + 5m - {m^2}\) trên \(\mathbb{R}\) bằng 6. Giải: a) Tìm m để giá trị nhỏ nhất của hàm số \(y = 4{x^2} - 4mx + {m^2} - m\) trên \(\mathbb{R}\) bằng 2 Do \(a = 4 > 0\) nên hàm số đạt giá trị nhỏ nhất \(y = - m\) tại \(x = \dfrac{m}{2}\). Khi đó, \(m = - 2\) b) Tìm m để giá trị lớn nhất của hàm số \(y = - 2{x^2} + 4mx + 5m - {m^2}\) trên \(\mathbb{R}\) bằng 6. Do \(a = - 2 < 0\) nên hàm số đạt GTLN \(y = {m^2} + 5m\) tại \(x = m\). \( \Rightarrow {m^2} + 5m = 6 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 6\end{array} \right.\) PHẦN 3 Phương trình – Hệ phương trình Bài 1: Giải và biện luận nghiệm của các phương trình sau theo m a) \(\left( {2{m^2} + 1} \right)x - m = x - 5\) b) \(m\left( {x - 2m} \right) = x - m - 1\) Bài 2. Giải và biện luận các phương trình theo m a) \(\left( {x - m} \right)\left( {mx + 2} \right) = 0\) b) \(\left( {x - 1} \right)\sqrt {x + 2m} = 0\) Bài 3. Giải và biện luận các phương trình theo tham số m a) \({x^2} + 2mx + 1 = 0\) b) \({x^2} - 2mx + m = 0\) c) \(m{x^2} + 3x + m = 0\) d) \({x^2} + 2m\left| x \right| + 1 = 0\) Bài 4. Tìm m nguyên để phương trình \({x^2} + 2mx + m - 3 = 0\) a) Có 2 nghiệm trái dấu. b) Có 2 nghiệm phân biệt dương. c) Vô nghiệm. d) Có nghiệm duy nhất âm. e) Có 2 nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \({x_1}^2 + {x_2}^2 = 6\) Bài 5. Biện luận số giao điểm của 2 parabol \(y = {x^2} + 2x + 2\) và \(y = - {x^2} + x - m\) theo tham số m. Vậy tập nghiệm của phương trình là \(S = \emptyset \) Bài 6. Giải phương trình a) \(\left| {x - 4} \right| = x - 2\) b) \({x^2} - 2x - \left| {x - 1} \right| - 3 = 0\) Bài 7. Giải và biện luận phương trình sau theo m: \(\left| {x + m} \right| = \left| {2x - 2} \right|\) Bài 8 Giải các phương trình sau a) \(\dfrac{{2x + 1}}{{3x + 1}} = \dfrac{{x + 1}}{{x - 2}}\) b) \(\dfrac{5}{{x - 2}} = \dfrac{{1 - x}}{{x - 2}} + 2\)
c) \(2 + \dfrac{2}{{x - 1}} = \dfrac{1}{{x + 2}} + \dfrac{1}{{{x^2} + x - 2}}\). d) \({x^8} - 5{x^2} + 2x + 2 = 0\) e) \(5{x^4} + 24{x^2} - 5 = 0\) Bài 9. Giải và biện luận các phương trình sau theo m a) \(\dfrac{{x - 3m}}{{x + 1}} = 0\) b) \(\dfrac{{mx - {m^2} - 1}}{{x - 2}} = 1\) c) \(\dfrac{m}{{mx - 1}} - \dfrac{2}{{x - m}} = 1\)
Bài 10. Tìm \(m\) để phương trình \({x^8} - \left( {2m + 5} \right){x^2} + \left( {{m^2} + 6m + 7} \right)x\)\( - 3{m^2} - 3 = 0\) (*) có ba nghiệm dương phân biệt. Bài 11. Giải các phương trình sau a) \(\sqrt {{x^2} - 1} = x - 2\) (đs: \(S = \emptyset \)) b) \(\sqrt {x + 8} = \sqrt x + x + 1\)(đs: \(S = \left\{ 1 \right\}\)) c) \(2{x^2} + 2x - \sqrt {4{x^2} + 4x - 1} = 0\)(đs: \(S = \left\{ {\dfrac{{ - 1 + \sqrt 3 }}{2};\dfrac{{ - 1 - \sqrt 3 }}{2}} \right\}\)) d) \(x - 2\sqrt {x + 3} + 5 = 0\)(đs: \(S = \emptyset \))
Bài 12. Giải và biện luận nghiệm phương trình theo tham số m a) Tìm m để phương trình \(\sqrt {{x^2} + mx + 2} = 2x + 1\) có hai nghiệm phân biệt.(đs: PT luôn có 2 nghiệm phân biệt với mọi m) b) Tìm m để phương trình \({\left( {2x - 1} \right)^2} + m = \sqrt {{x^2} - x + 1} \) có nghiệm.(đs: \(m \le \dfrac{{49}}{{16}}\)) c) Tìm m để phương trình \(3\sqrt {x - 1} + m\sqrt {x + 1} = 2\sqrt[4]{{{x^2} - 1}}\) có nghiệm.(đs: \(m \le \dfrac{1}{3}\)). Bài 13:Giải hệ phương trình a) \(\left\{ \begin{array}{l}2x - y = 3\\x + 2y = 5\end{array} \right.\) b) \(\left\{ \begin{array}{l}5x + 2y = - 6\\ - x + y = 2\end{array} \right.\) c) \(\left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 8\\2xy + x + y = 7\end{array} \right.\) Đáp án: \(\left( {2;1} \right);\left( {1;2} \right);\left( { - 2; - 3} \right);\left( {6; - 5} \right)\)
d) \(\left\{ \begin{array}{l}{x^2} - {y^2} = 32\\xy = 12\end{array} \right.\) Đáp án: \(\left( {6;2} \right);\left( { - 6; - 2} \right)\) e) \(\left\{ \begin{array}{l}{x^2} + {y^2} - xy = 3\\{x^2} + {y^2} + x + y = 8\end{array} \right.\) (đs: (2;1);(1;2)) f) \(\left\{ \begin{array}{l}x + y + \dfrac{1}{x} + \dfrac{1}{y} = - 4\\{x^2} + {y^2} + \dfrac{1}{{{x^2}}} + \dfrac{1}{{{y^2}}} = 4\end{array} \right.\) (đs: (-1;-1) g) \(\left\{ \begin{array}{l}{x^2} - x = y\\{y^2} - y = x\end{array} \right.\) (đs: (0;0);(2;2)) h) \(\left\{ \begin{array}{l}\sqrt {x + 3} + \sqrt {1 - y} = 2\\\sqrt {y + 3} + \sqrt {1 - x} = 2\end{array} \right.\)(đs: (1;1);(-3;-3)) Bài 14. Tìm điều kiện tham số để các hệ sau có nghiệm. a) \(\left\{ \begin{array}{l}\sqrt {x - 1} + \sqrt y = 3\\x + y = 2m\end{array} \right.\) Đáp án: \(\dfrac{{11}}{4} \le m \le 5\). b) \(\left\{ \begin{array}{l}\sqrt x + \sqrt y = m\\x\sqrt x + y\sqrt y = {m^3} - 3m\end{array} \right.\) Đáp án: \(m \ge 2\) PHẦN 4 Vectơ Bài 1. Cho 4 điểm A, B, C, D. Gọi I, J lần lượt là trung điểm của AD và BC. Chứng minh rằng: a) \(\overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {JA} + \overrightarrow {JD} = \overrightarrow 0 \) b) Gọi G là trung điểm của IJ. Chứng minh. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Bài 2. Cho tam giác ABC. Gọi M là trung điểm của AB, D là trung điểm của BC, N là điểm thuộc AC sao cho \(\overrightarrow {CN} = 2\overrightarrow {NA} \). K là trung điểm của MN. Phân tích vectơ. a) \(\overrightarrow {AK} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \) (đs \(\overrightarrow {AK} = \dfrac{1}{4}\overrightarrow {AB} + \dfrac{1}{6}\overrightarrow {AC} \)) b) \(\overrightarrow {KD} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \) (đs \(\overrightarrow {KD} = \dfrac{1}{4}\overrightarrow {AB} + \dfrac{1}{3}\overrightarrow {AC} \)) Bài 3. Cho \(\overrightarrow a = \left( { - 1;0} \right);\overrightarrow b = \left( { - 1;1} \right);\)\(\overrightarrow c = \left( {3;4} \right)\). a) Tìm toạ độ của vectơ \(\overrightarrow d = 2\overrightarrow a + 3\overrightarrow b + 5\overrightarrow c \). (đs \(\overrightarrow d = (10;23)\)) b) Tìm 2 số m, n sao cho \(m\overrightarrow a + n\overrightarrow b + 2\overrightarrow d = \overrightarrow 0 \). (đs \(m = 66;n = - 46\)) c) Biểu diễn vectơ \(\overrightarrow a \) theo \(\overrightarrow b \) và \(\overrightarrow c \). (đs \(\overrightarrow a = \dfrac{4}{7}\overrightarrow b - \dfrac{1}{7}\overrightarrow c \)) Bài 4. Trong mặt phẳng tọa độ, cho các điểm \(A(0;2);B( - 4;4);C(3;0)\). a) Chứng minh ba điểm A, B, C tạo thành một tam giác. b) Tìm tọa độ trọng tâm G của tam giác ABC. (đs: \(G\left( { - \dfrac{1}{3};2} \right)\)) PHẦN 5 Tích vô hướng và ứng dụng Bài 1. Cho tam giác ABC có A(1; 2), B(–2; 6), C(9; 8). a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \). Chứng minh tam giác ABC vuông tại A. (đs: \(\overrightarrow {AB} .\overrightarrow {AC} = 48\)) b) Tính chu vi, diện tích tam giác ABC. (đs: Chu vi: \(15 + 5\sqrt 5 \); DT: 25) c) Tìm toạ độ điểm M trên Oy để B, M, A thẳng hàng. (đs:\(M\left( {0;\dfrac{{10}}{3}} \right)\)) d) Tìm toạ độ điểm D để ABDC là hình chữ nhật. (đs: D(6;12)) e) Tìm toạ độ điểm I thoả \(\overrightarrow {IA} + 2\overrightarrow {IB} - \overrightarrow {IC} = \overrightarrow 0 \) (đs: IPNB là hình bình hành với N là trung điểm của BC, P là trung điểm của AB). f) Phân tích vectơ \(\overrightarrow {AI} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \) (đs: \(\overrightarrow {AB} - \dfrac{1}{2}\overrightarrow {AC} \)). Bài 2. Trong mặt phẳng tọa độ, cho hai vectơ \(\overrightarrow a = \left( { - 2;3} \right),\overrightarrow b = \left( {\dfrac{1}{2};2} \right)\) a) Tính tích vô hướng và tìm góc giữa hai vectơ\(\overrightarrow a \) và \(\overrightarrow b \). (đs: \(\overrightarrow a .\overrightarrow b = 5;\left( {\overrightarrow a ,\overrightarrow b } \right) = \dfrac{{10\sqrt {221} }}{{\sqrt {221} }}\)) b) Tìm m để vectơ \(\overrightarrow u = m\overrightarrow a - \overrightarrow b \) song song với trục hoành. (đs: \(m = \dfrac{2}{3}\)) c) Tìm n để vectơ \(\overrightarrow v = \overrightarrow a + 2n\overrightarrow b \) tạo với vectơ \(\overrightarrow a \) một góc \(45^\circ \). (đs: n=0) HocTot.XYZ
|