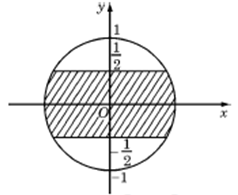
Đề kiểm tra 45 phút (1 tiết) - Đề số 1 – Chương IV - Giải tích 12Đáp án và lời giải chi tiết Đề kiểm tra 45 phút (1 tiết) - Đề số 1 – Chương IV - Giải tích 12. Đề bài Câu 1. Tìm tập nghiệm S của phương trình \({z^3} + {z^2} - 2 = 0\) trên trường số phức. A. \(S = \{ - 1 - i,\, - 1 + i\} \). B. \(S = \{ 1,\,1 - i,\,1 + i\} \). C. \(S = \{ 1,\, - 1 - i,\, - 1 + i\} \). D. \(S = \{ 1\} \). Câu 2. Tính mô đun của số phức \(z\dfrac{{1 + 2i}}{{1 - i}}\). A. \(|z| = \dfrac{{\sqrt 5 }}{2}\). B. \(|z| = \sqrt {10} \). C. \(|z| = \dfrac{5}{2}\). D. \(|z| = \dfrac{{\sqrt {10} }}{2}\). Câu 3. Số phức \(z = \dfrac{{1 - i}}{{1 + i}} - 3 + 4i\) có số phức liên hợp là: A. \(\overline z = - 3i\). B. \(\overline z = - 3\). C. \(\overline z = - 3 + 3i\). D. \(\overline z = - 3 - 3i\). Câu 4. Trên mặt phẳng tọa độ, để tập hợp điểm biểu diễn các số phức z nằm trong phần gạch chéo ( kể cả biên ) ở hình vẽ dưới đây thì điều kiện của z là: A. \(|z| \le 1\) và phần ảo thuộc đoạn \(\left[ { - \dfrac{1}{2};\dfrac{1}{2}} \right]\). B. \(|z| \le \dfrac{1}{2}\)và phần thực thuộc đoạn \(\left[ { - \dfrac{1}{2};\dfrac{1}{2}} \right]\). C. \(|z| \le \dfrac{1}{2}\) và phần ảo thuộc đoạn \(\left[ { - \dfrac{1}{2};\dfrac{1}{2}} \right]\). D. \(|z| \le 1\) và phần thực thuộc đoạn \(\left[ { - \dfrac{1}{2};\dfrac{1}{2}} \right]\). Câu 5. Mô đun của số phức z thỏa mãn \(z + \left( {2 + i} \right)\overline z = 3 + 5i\) là: A. \(\sqrt {17} \) B. \(\sqrt {15} \) C. \(\sqrt {13} \) D. \(\sqrt {14} \). Câu 6. Trong tập số phức C, chọn phát biểu đúng . A. \(z + \overline z \) là số thuần ảo. B. \(\overline {{z_1} + {z_2}} = \overline {{z_1}} + \overline {{z_2}} \). C. \({z^2} - {\left( {\overline z } \right)^2} = 4ab\). D. \(|{z_1} + {z_2}| = |{z_1}| + |{z_2}|\). Câu 7. Gọi \({z_1}\,,\,{z_2}\) lần lượt là nghiệm của phương trình \({z^2} + 2z + 10 = 0\). Tính \(|{z_1}{|^2} + |{z_2}{|^2}\). A. 20 B. 50 C. 100 D. 15 Câu 8. Cho số phức z = 2 + 3i. Giá trị của \(|2iz - \overline z |\) bằng : A. 15 B. \(\sqrt {15} \) C. 113 D. \(\sqrt {113} \). Câu 9. Trên mặt phẳng tọa độ, điểm biểu diễn của số phức z = - 5 – 6i là điểm nào sau đây ? A. P(5 ; - 6). B. Q(5 ; 6). C. M(- 5 ; 6). D. N(- 5 ; - 6 ). Câu 10. Tìm số phưc liên hợp của số phức \(z = 1 - 9i\). A. \(\overline z = - 1 - 9i\). B. \(\overline z = - 1 + 9i\). C. \(\overline z = 1 - 9i\). D. \(\overline z = 1 + 9i\). Câu 11. Số phức z là số thực nếu: A. a = 0. B. b = 0. C. i = 0. D. a. b = 0. Câu 12. Các số thực x , y thỏa mãn \(\dfrac{{x - 3}}{{3 + i}} + \dfrac{{y - 3}}{{3 - i}} = i\). Khi đó tổng T = x + y bằng : A. 4 B. 5 C. 6 D. 7 Câu 13. Cho biểu thức \(|z| + z = 3 + 4i\). Số phức z là : A. \(z = \dfrac{7}{6} - 4i\). B. \(z = \dfrac{6}{7} + 4i\). C. \(z = - \dfrac{7}{6} - 4i\). D. \(z = - \dfrac{7}{6} + 4i\). Câu 14. Cho số phức z thỏa mãn \(|z - 2 - 2i| = 1\). Số phức z - i có mô đun nhỏ nhất là: B. \(1 - \sqrt 5 \). C. \(\sqrt 5 + 1\). D. \(\sqrt 5 + 2\). Câu 15. Cho hai số phức \({z_1} = 1 + 2i\,,\,\,{z_2} = 2 - 3i\). Phần thực và phần ảo của số phức \(w = 3{z_1} - 2{z_2}\) là: A. 1 và 12. B. – 1 và 12. C. – 1 và 12i. D. 1 và 12i. Câu 16. Cho số phức z thỏa mãn \(|z + 3| + |z - 3| = 10\). Giá trị nhỏ nhất của \(|z|\) là: A. 3 B. 4 C. 5 D. 6 Câu 17. Nghiệm của phương trình \(2{z^4} + {z^2} - 1 = 0\) trên tập số phức là: A. \(z = \pm i\). B. \(\left[ \begin{array}{l}z = \dfrac{{\sqrt 2 }}{2}\\z = i\end{array} \right.\). C. \(\left[ \begin{array}{l}z = \pm \dfrac{i}{{\sqrt 2 }}\\z = \pm i\end{array} \right.\). D. \(\left[ \begin{array}{l}z = \pm \dfrac{1}{{\sqrt 2 }}\\z = \pm i\end{array} \right.\). Câu 18. Tập hợp các điểm biểu diễn số phức z thỏa mãn \(|z| = |2 + 2i|\) là: A. Đường tròn bán kính \(2\sqrt 2 \). B. Đường tròn bán kính 4. C. Đường tròn bán kính 2. D. Đường tròn bán kính \(4\sqrt 2 \). Câu 19. Số phức z có mô đun r và acgumen \(\varphi \) thì có dạng lượng giác là: A. \(z = r\left( {\cos \varphi + i\sin \varphi } \right)\). B. \(z = r\left( {\cos \varphi - i\sin \varphi } \right)\). C. \(z = r\left( {\sin \varphi + i\cos \varphi } \right)\). D. \(z = r\left( {\sin \varphi - i\cos \varphi } \right)\). Câu 20. Tổng của hai số phức \({z_1} = 1 - 2i\,,\,\,{z_2} = 2 + 3i\) là: A. \(2 - 5i\). B. 2 + 5i. C. 3 + i. D. 3 + 5i. Câu 21. Gọi \(\varphi \) là 1 acgumen cảu số phức z có biểu diễn là \(M\left( {\dfrac{1}{2};\dfrac{{\sqrt 3 }}{2}} \right)\)nằm trên đường tròn đơn vị, số đo nào sau đây có thể là một acgumen của z ? A. \(\dfrac{\pi }{2}\) B. \(\dfrac{\pi }{3}\) C. \(\dfrac{\pi }{4}\) D. \(\dfrac{\pi }{6}\). Câu 22. Cho số phức z thỏa mãn \(|z + 1 - i|\,\, \le \,3\)là số thực. Tập hợp điểm M biểu diễn số phức z là: B. Đường thẳng . C. Hình tròn . D. Một điểm duy nhất. Câu 23. Cho hai số phức \({z_1} = 4 + 5i\,,\,\,{z_2} = 1 + 2i\). Tìm khẳng định đúng ? A. \({z_1} + {z_2} = 5 + 7i\). B. \({z_1} - {z_2} = 3 + 4i\). C. \({z_1}.{z_2} = 10 + 3i\). D. \({z_1}.{z_2} = 20 + 5i\). Câu 24. Tìm điểm M biểu diễn số phức z = 2 + 2i. A. M ( 2 ; - 2). B. M (2 ; 2). C. M ( -2 ; 2). D. M (-2 ; 2). Câu 25. Cho số phức z có dạng lượng giác \(z = 4\left( {\cos \left( { - \dfrac{\pi }{2}} \right) + i\sin \left( { - \dfrac{\pi }{2}} \right)} \right)\). Dạng đại số của z là : A. z = 4. B. z = - i. C. z = 4i. D. z = - 4i.
Lời giải chi tiết
Lời giải chi tiết Câu 1: (C) \(\begin{array}{l}{z^3} - {z^2} - 2 = 0\\ \Leftrightarrow \left( {z - 1} \right)\left( {{z^2} + 2z + 2} \right)\\ \Leftrightarrow \left[ \begin{array}{l}z - 1 = 0\\{z^2} + 2z + 2 = 0\end{array} \right.\end{array}\)\(\) Giải pt (2) Ta có \(\Delta = {(b')^2} - a.c = 1 - 2 = - 1 = {i^2}\) \(\Delta \) có hai căn bậc hai là i và – i Nghiệm của pt (2) là \({x_1} = - 1 - {\rm{ }}i\) và Tập nghiệm S trên trường số phức là: S={ 1, -1- i, -1+ i} Câu 2: (D) \(\begin{array}{l}z = \dfrac{{1 + 2i}}{{1 - i}} = \dfrac{{\left( {1 + 2i} \right).\left( {1 + i} \right)}}{{\left( {1 - i} \right)\left( {1 + i} \right)}}\\\,\,\,\, = \dfrac{{1 + 3i + 2.{i^2}}}{{1 - {i^2}}} = \dfrac{{ - 1 + 3.i}}{2}\\\,\,\,\, = \dfrac{{ - 1}}{2} + \dfrac{3}{2}i\\ \Rightarrow \left| z \right| = \sqrt {{{\left( { - \dfrac{1}{2}} \right)}^2} + {{\left( {\dfrac{3}{2}} \right)}^2}} = \dfrac{{\sqrt {10} }}{2}\end{array}\) Câu 3: (D) \(\begin{array}{l}z = \dfrac{{1 - i}}{{1 + i}} - 3 + 4i\\\,\,\,\,\, = \dfrac{{{{\left( {1 - i} \right)}^2}}}{{1 - {i^2}}} - 3 + 4i\\\,\,\,\,\, = - i - 3 + 4i = - 3 + 3i\end{array}\) Số phức liên hợp của z là: \(\overline z = - 3 - 3i\) Câu 4: (A) Câu 5: (C) Đặt z = a + bi \(a,b \in \mathbb{Z}\) \(\begin{array}{l}z + \left( {2 + i} \right)\overline z = 3 + 5i\\ \Leftrightarrow \left( {a + bi} \right) + \left( {2 + i} \right)\left( {a - bi} \right) = 3 + 5i\\ \Leftrightarrow 3a + b + ai - bi = 3 + 5i\\ \Leftrightarrow 3a + b + \left( {a - b} \right)i = 3 + 5i\\ \Leftrightarrow \left\{ \begin{array}{l}3a + b = 3\\a - b = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 3\end{array} \right.\left( {tm} \right)\\ \Rightarrow z = 2 - 3i\\ \Rightarrow \left| z \right| = \sqrt {{2^2} + {{\left( { - 3} \right)}^2}} = \sqrt {13} \end{array}\) Câu 6: (B) Câu 7: (A) \({z^2} + 2z + 10 = 0\) Có \(\Delta ' = {\left( {b'} \right)^2} - ac = 1 - 10 = - 9 = {\left( {3i} \right)^2}\) \(\Delta \) có hai căn bậc hai là 3i và – 3i Phương trình có hai nghiệm \({z_1} = {\rm{ }} - 1{\rm{ }} + {\rm{ }}3i\) và \({z_2} = {\rm{ }} - 1{\rm{ }}--{\rm{ }}3i\) \(\begin{array}{l}\left| {{z_1}} \right| = \left| {{z_2}} \right| = \sqrt {10} \\ \Rightarrow {\left| {{z_1}} \right|^2} = {\left| {{z_2}} \right|^2} = 10\\ \Rightarrow {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = 20\end{array}\) Câu 8: (D) \(\begin{array}{l}z{\rm{ }} = {\rm{ }}2{\rm{ }} + {\rm{ }}3i\\ \Rightarrow 2iz - \overline z = {\rm{ }}2i\left( {2{\rm{ }} + 3i} \right){\rm{ }}--{\rm{ }}\left( {2{\rm{ }}--{\rm{ }}3i} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 4i - 6 - 2 + 3i\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - 8 + 7i\end{array}\) Câu 9: (D) Câu 10: (D) Câu 11: (B) Câu 12: (C) \(\begin{array}{l}\dfrac{{x - 3}}{{3 + i}} + \dfrac{{y - 3}}{{3 - i}} = i\\ \Leftrightarrow \left( {x - 3} \right)\left( {3 - i} \right) + \left( {y - 3} \right)\left( {3 + i} \right) = i\left( {3 - i} \right)\left( {3 + i} \right)\\ \Leftrightarrow 3\left( {x - 3} \right) - \left( {x - 3} \right)i + 3\left( {y - 3} \right) + \left( {y - 3} \right)i = 10i\\ \Leftrightarrow 3\left( {x + y - 6} \right) + \left( {y - x} \right)i = 10i\\ \Leftrightarrow \left\{ \begin{array}{l}x + y - 6 = 0\\y - x = 10\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + y = 6\\y - x = 10\end{array} \right.\end{array}\) Câu 13: (D) Đặt \(z = a + bi;\,\,\,\,a,b \in \mathbb{Z}\) \(\begin{array}{l}|z| + z = 3 + 4i\\ \Rightarrow \sqrt {{a^2} + {b^2}} + a + bi = 3 + 4i\\\left\{ \begin{array}{l}\sqrt {{a^2} + {b^2}} + a = 3{\rm{ (1)}}\\b = 4{\rm{ (2)}}\end{array} \right.\end{array}\) Thay (2) v ào (1) ta được: \(\begin{array}{l}\sqrt {{a^2} + {{16}^2}} + a = 3\\ \Leftrightarrow \sqrt {{a^2} + {{16}^2}} = 3 - a\\ \Leftrightarrow \left\{ \begin{array}{l}a \le 3\\6a = - 7\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a \le 3\\a = \dfrac{{ - 7}}{6}\end{array} \right.\\ \Leftrightarrow a = \dfrac{{ - 7}}{6}\\ \Rightarrow z = - \dfrac{7}{6} + 4i\end{array}\) Câu 14: (A) Đặt z = x +yi M(x,y) \(x,y \in \mathbb{Z}\) \(\begin{array}{l}|z - 2 - 2i| = 1\\ \Leftrightarrow |x + yi - 2 - 2i| = 1\\ \Leftrightarrow \left| {\left( {x - 2} \right) + \left( {y - 2} \right)i} \right| = 1\\ \Leftrightarrow \sqrt {{{\left( {x - 2} \right)}^2} + {{(y - 2)}^2}} = 1\\ \Leftrightarrow {\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 1\end{array}\)=1 Điểm M biểu diễn cho số phức z nằm trên đường tròn tâm I(2,2), bán kính r = 1 Ta lại có: \(\left| {z--i} \right| = \left| {x + yi--i} \right| \)\(\,= \left| {x + \left( {y--1} \right)} \right| = \sqrt {{x^2} + {{(y - 1)}^2}} \) Lấy H(0, 1) suy ra \(HM = \sqrt {{x^2} + {{(y - 1)}^2}} \) Do M chạy trên đường tròn, H cố định nên MH nhỏ nhất khi M là giao điểm của HI với đường tròn. Có H(0,1) , I(2,2) nên \(\overrightarrow {HI} = \left( {2;1} \right)\) = (2,1) Pt đường thẳng HI: (1) \(\left\{ \begin{array}{l}x = 2t\\y = 1 + t\end{array} \right.\) Mặt khác, HI giao với đường tròn tại M nên thay (1) vào pt đường tròn ta được : \(\begin{array}{l}{\left( {2t - 2} \right)^2} + {\left( {t - 1} \right)^2} = 1\\ \Leftrightarrow 5{\left( {t - 1} \right)^2} = 1\\ \Leftrightarrow {\left( {t - 1} \right)^2} = \dfrac{1}{5}\\ \Leftrightarrow \left[ \begin{array}{l}t - 1 = \dfrac{1}{{\sqrt 5 }}\\t - 1 = - \dfrac{1}{{\sqrt 5 }}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = 1 + \dfrac{1}{{\sqrt 5 }}\\t = 1 - \dfrac{1}{{\sqrt 5 }}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{M_1} = \left( {2 + \dfrac{2}{{\sqrt 5 }},2 + \dfrac{1}{{\sqrt 5 }}} \right)\\{M_2} = \left( {2 - \dfrac{2}{{\sqrt 5 }},2 - \dfrac{1}{{\sqrt 5 }}} \right)\end{array} \right.\\\\\end{array}\) Có \(H{M_1} = \sqrt 5 + 1;\,\,H{M_2} = \sqrt 5 - 1\) \(|z - i{|_{\min }} \Leftrightarrow |z - i| = H{M_2} = \sqrt 5 - 1\) với \({M_2} = \left( {2 - \dfrac{2}{{\sqrt 5 }},2 - \dfrac{1}{{\sqrt 5 }}} \right)\) Câu 15: (B) \(\begin{array}{l}w = 3{z_1}--2{z_2}\\\,\,\,\,\,\, = 3\left( {1{\rm{ }} + {\rm{ }}2i} \right)--2\left( {2--3i} \right)\\\,\,\,\,\,\, = 3 + 6i - 4 + 6i\\\,\,\,\,\,\, = - 1 + 12i\end{array}\) Phần thực: -1 , phần ảo: 12 Câu 16: (B) Đặt \(z = a + bi;\,\,\,\,a,b \in \mathbb{Z}\) \(\begin{array}{l}\left| {z + 3} \right| + \left| {z--3} \right| = 10\\ \Leftrightarrow |a + bi + 3| + |a + bi - 3| = 10\\ \Leftrightarrow \sqrt {{{(a + 3)}^2} + {b^2}} + \sqrt {{{(a - 3)}^2} + {b^2}} = 10\end{array}\) Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki ta có: \(10 = \sqrt {{{(a + 3)}^2} + {b^2}} + \sqrt {{{(a - 3)}^2} + {b^2}} \)\(\,\le \sqrt {2{\rm{[}}{{(a + 3)}^2} + {b^2} + {{(a - 3)}^2} + {b^2}{\rm{]}}}\) \(\begin{array}{l} \Leftrightarrow \sqrt {2\left( {2{a^2} + 2{b^2} + 18} \right)} \ge 10\\ \Leftrightarrow {a^2} + {b^2} + 9 \ge 25\\ \Leftrightarrow {a^2} + {b^2} \ge 16\\ \Leftrightarrow \sqrt {{a^2} + {b^2}} \ge 4\\ \Leftrightarrow |z| \ge 4\\ \Leftrightarrow |z{|_{\min }} = 4\end{array}\) Câu 17: (D) \(\begin{array}{l}2{z^4} + {z^2} - 1 = 0\\\Delta = {b^2} - 4ac = 1 + 4.2 = 9\end{array}\) Nghiệm của phương trình là: \(\begin{array}{l}\left[ \begin{array}{l}{z^2} = \dfrac{{ - 1 - 3}}{4} = - 1 = {i^2}\\{z^2} = \dfrac{{ - 1 + 3}}{4} = \dfrac{1}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}z = \pm i\\z = \pm \dfrac{1}{{\sqrt 2 }}\end{array} \right.\end{array}\) Câu 18: (A) \(\left| z \right| = \left| {2 + 2i} \right| = 2\sqrt 2 \) Đặt z= a+ bi \(\begin{array}{l}|z| = 2\sqrt 2 \\ \Leftrightarrow |a + bi| = 2\sqrt 2 \\ \Leftrightarrow \sqrt {{a^2} + {b^2}} = 2\sqrt 2 \end{array}\) Tập hợp các điểm biểu diễn cho số phức z là đường tròn có tâm O(0,0), bán kính \(r = 2\sqrt 2 \) Câu 19: (A) Câu 20: (C) \({z_1} + {z_2} = 1--2i + 2 + 3i = 3 + i\) Câu 21: (B) Câu 22: (C) Đặt z = x + yi \(\begin{array}{l}|z + 1 - i| \le 3\\ \Leftrightarrow |x + yi + 1 - i| \le 3\\ \Leftrightarrow \left| {\left( {x + 1} \right) + \left( {y - 1} \right) \le 3} \right|\\ \Leftrightarrow \sqrt {{{\left( {x + 1} \right)}^2} + {{\left( {y - 1} \right)}^2}} \le 3\end{array}\) Điểm biểu diễ số phức z là một hình tròn tâm I(-1,1), bán kính \(r = 3\) Câu 23: (A) \({z_1} + {z_2} = 4 + 5i + 1 + 2i = 5 + 7i\) Câu 24: (B) Câu 25: (D) HocTot.XYZ
|