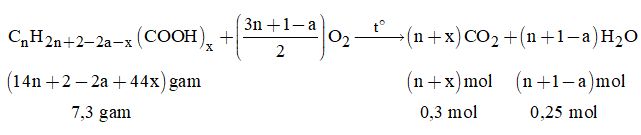Đề kiểm tra 15 phút - Đề số 2 - Chương IX - Hóa học 11Đáp án và lời giải chi tiết Đề kiểm tra 15 phút - Đề số 2 - Chương IX - Hóa học 11. Đề bài Câu 1. Công thức nguyên của một axit hữu cơ, mạch hở có dạng (C2H3O2)n. Hãy biện luận tìm công thức phân tử, viết công thức cấu tạo axit, biết axit này này mạch không phân nhánh và đọc tên. Câu 2. Công thức nguyên của một anđehit mạch hở, chưa no chứa một nối ba trong phân tử có dạng (C4H4O)n. Biện luận tìm công thức phân tử anđehit trên. Câu 3. Đốt cháy hoàn toàn 7,3 gam một axit đa chức thu được 0,3 mol CO2; 0,25 mol H2O. Hãy lập công thức phân tử, công thức câu tạo và gọi tên axit đó (biết mạch cacbon không phân nhánh). Lời giải chi tiết Câu 1. + Cách 1. Công thức đã cho có thể viết: C2nH3nO2n. Vì axit no nên số liên kết \(\pi \) bằng với số nhóm COOH ( mỗi nhóm COOH có một liên kết \(\pi \)). Axit C2nH3nO2n phải có n chức COOH, tức n liên kết \(\pi \). Suy ra: \(n = \dfrac{{2.2n - 3n + 2}}{2} \) \(\Leftrightarrow 2n = n + 2 \Rightarrow n = 2\) Vậy công thức phân tử cần tìm là C4H6O2 ứng với công thức cấu tạo \(HOOC - C{H_2} - C{H_2} - COOH\) (axit succinic). + Cách 2. Công thức axit đã cho có thể viết C2nH3nO2n hay CnH2n(COOH)n Vì axit no nên: số hiđro + số nhóm chức = \(2 \times \) số cacbon + 2 \( \Leftrightarrow 2n + n = 2n + 2 \Rightarrow n = 2\) Câu 2. + Cách 1. Công thức anđehit trên có thể viết: C4nH4nOn. Anđehit này có n nhóm –CHO nên chứa n liên kết \(\pi \). Mặt khác nó cũng chứa 2 liên kết \(\pi \) ở nối ba chưa no, nên suy ra: \(n + 2 = \dfrac{{2.4n - 4n + 2}}{2} \Rightarrow n = 1\) Vậy công thức phân tử cần tìm là C4H4O. + Cách 2. Công thức anđehit có thể viết C2nH3nO2n hay C3nH3n(CHO)n Anđehit chưa no có 1 nối ba nên: Số hiđro + số nhóm chức\(2 \times \) số cacbon – 2 \( \Leftrightarrow 3n + n = 2.3n - 2 \Rightarrow n = 1\) Vậy công thức phân tử của anđehit: C4H4O. Câu 3. + Cách 1. Gọi công thức tổng quát của axit là: CnH2n+2-2a-x(COOH)x Phản ứng:
Ta có hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{{14 + 2 - 2a + 44x}}{{7,3}} = \dfrac{{n + x}}{{0,3}}\\\dfrac{{14n + 2 - 2a + 44x}}{{7,3}} = \dfrac{{n + 1 - a}}{{0,25}}\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}31n - 59x + 6a = 6{\rm{ }}\left( 1 \right)\\38n - 68a - 110x = 68{\rm{ }}\left( 2 \right)\end{array} \right.\) Giải (1) và (2) \( \Rightarrow 77,87x = 38,93n\) Khi \(x = 2 \Rightarrow n = 4;a = 0\) \(\Rightarrow \) CTPT: C4H8(COOH)2 Khi \(x = 3 \Rightarrow n = 6;a < 0\) (loại) + Cách 2. Sử dụng định luật bảo toàn khối lượng Ta có: \({n_C} = {n_{C{O_2}}} = 0,3\left( {mol} \right);\) \({n_H} = {n_{{H_2}O}} = 2 \times 0,25 = 0,5\left( {mol} \right)\) \( {n_O} = \left[ {7,3 - \left( {0,3 \times 12 + 0,5.1} \right)} \right]:16 \)\(\,= 0,2\left( {mol} \right)\) Gọi công thức tổng quát của axit: (C3H5O2)n hay C2cH4n(COOH)n Điều kiện: \(4n \le 2n \times 2 + 2 - n \Rightarrow n \le 2\) Nghiệm hợp lí: \(n = 2 \Rightarrow \) CTPT axit: C4H8(COOH)2 Công thức cấu tạo: \(HOOC - {\left( {C{H_2}} \right)_4} - COOH\): axit ađipic. HocTot.XYZ
|