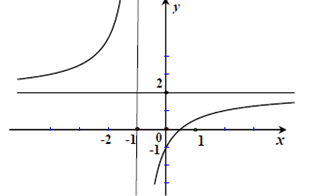
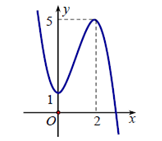
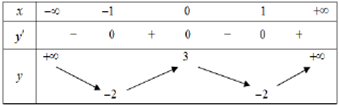
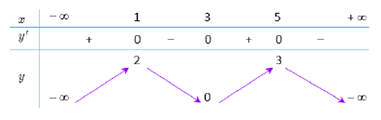
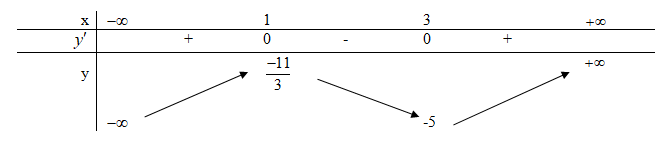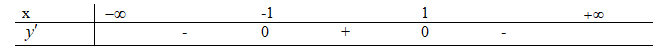Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương I - Giải Tích 12Đáp án và lời giải chi tiết Đề thi kiểm tra 45 phút và 1 tiết - Đề số 2 - Chương I - Giải Tích 12 Đề bài Câu 1. Đồ thị sau đây là của hàm số nào? A. \(y = \dfrac{{1 - 2x}}{{x - 1}}\) B. \(y = \dfrac{{2x + 1}}{{x + 1}}\) C. \(y = \dfrac{{2x + 1}}{{x - 1}}\) D. \(y = \dfrac{{2x - 1}}{{x + 1}}\) Câu 2. Đồ tị hàm số \(y = {x^3} - 3{x^2} + 1\) cắt đường thẳng y = m tại ba điểm phân biệt thì tất cả các giá trị tham số m thỏa mãn là A. m > 1 B. \( - 3 \le m \le 1\) C. -3 < m < 1 D. m < - 3. Câu 3. Đường thẳng y = x – 1 cắt đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x + 1}}\) tại các điểm có tọa độ là: A. (0 ; - 1), (2 ; 1) B. (0 ; 2) C. (1 ; 2) D. (- 1 ; 0), (2 ; 1). Câu 4. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số \(y = \dfrac{{{x^3}}}{ 3} - 2{x^2} + 3x - 5\). A. Song song với trục tung B. Có hệ số góc dương C. Có hệ số góc âm D. Song song với trục hoành. Câu 5. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{1 - 4x} }{ {2x - 1}}\). A. y = 2 B. y = 4 C. y =1/2 D. y = - 2 . Câu 6. Đường cong trong hình dưới đây là đồ thị của hàm số nào ?
A. \(y = - {x^3} + 2{x^2} - 1\) B. \(y = {x^3} - 3{x^2} + 1\) C. \(y = - {x^3} + 3{x^2} + 1\) D. \(y = - {x^3} + 3{x^2} - 4\). Câu 7. Cho hàm số y = f(x) có bảng biến thiên như sau. Hàm số đã cho nghịch biến trên khoảng nào sau đây ?
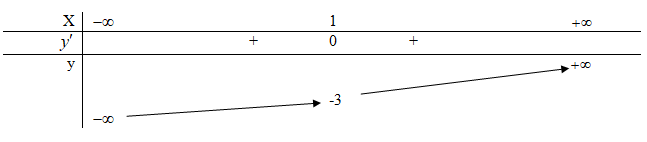
A. (0 ; 1) B. \(( - \infty ;0)\) C. \((1; + \infty )\) D. (- 1 ; 0). Câu 8. Tìm tất cả các giá trị của m để dồ thị hàm số \(y = {x^3} - 3x + 2\) cắt đường thẳng y = m – 1 tại ba điểm phân biệt . A. 0 < m < 4 B. \(1 < m \le 5\) C. \(1 < m < 5\) D. \(1 \le m < 5\). Câu 9. Đồ thị hàm số nào sau đây có tâm đối xứng là điểm I(1 ; -2 ) ? A. \(y = \dfrac{{2x - 3} }{ {2x + 4}}\) B. \(y = 2{x^3} - 6{x^2} + x + 1\) C. \(y = - 2{x^3} + 6{x^2} + x - 1\) D. \(y =\dfrac {{2 - 2x} }{{1 - x}}\). Câu 10. Cho hàm số y = f(x) có bảng biến thiên cho bởi bảng sau:
Kết luận nào sau đây sai? A. Giá trị cực tiểu của hàm số bằng 3. B. f(x) đồng biến trên mỗi khoảng \(( - \infty ;1),\,(3;5)\). C. Điểm cực đại của đồ thị hàm số là (1 ; 2), (5 ; 3). D. f(x) nghịch biến trên môĩ khoảng \((1;3),\,(5; + \infty )\). Câu 11. Cho hàm số \(y = \dfrac{3 }{{x - 2}}\). Số tiệm cận của đồ thị hàm số bằng : A. 0 B. 2 C. 3 D. 1 Câu 12. Đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{1 - 2x} }{ { - x + 2}}\) là: A. x= - 2; y= - 2. B. x= 2; y = - 2 C. x = - 2; y= 2 D. x = 2; y = 2 Câu 13. Hàm số \(y = {x^3} - 3{x^2} + 3x - 4\) có bao nhiêu cực trị ? A 1 B. 2 C. 0 D. 3 Câu 14. Giá trị cực đại của hàm số \(y = {x^3} - 12x - 1\). A. – 17 B. – 2 C. 45 D. 15 . Câu 15. Đồ thi hàm số nào dưới đây có tiệm cận đứng A. \(y = x\) B. \(y = {x^3-2x^2+1}\) C. \(y = \dfrac{{2x} }{ {x - 1}}\) D. \(y = \dfrac{\pi }{ {{x^2} - x + 1}}\). Câu 16. Cho hàm số \(y = \dfrac{{x + 1} }{ {x - 1}}\). Khẳng định nào sau đây là đúng ? A. Hàm số đã cho nghịch biến trên khoảng \(( - \infty ;1)\). B. Hàm số đã cho đồng biến trên khoảng \(( - \infty ;1),\,(1; + \infty )\). C. Hàm số đã cho đồng biến trên khoảng \((0; + \infty )\). D. Hàm số đã cho nghịch biến trên tập R. Câu 17. Cho hàm số y = f(x) xác định trên khoảng \((0; + \infty )\) và thỏa mãn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 1\). Hãy chọn mệnh đề đúng trong các mệnh đề sau : A. Đường thẳng x = 1 là tiệm cận ngang của đồ thị hàm số y = f(x). B. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số y = f(x). C. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số y = f(x). D. Đường thẳng y = 1 là tiệm cận đứng của đồ thị hàm số y = f(x). Câu 18. Hàm số \(y = - {x^3} + 3x - 5\) đồng biến trên khoảng nào ? A. \(( - \infty ; - 1)\) B. \(( - 1;1)\) C. \((1; + \infty )\) D. \(( - \infty ;1)\) Câu 19. Trong các hàm số sau, hàm số nào luôn nghịch biến trên R ? A. \(y = \sin x - x\) B. \(y = - {x^3} + 3{x^2}\) C. \(y =\dfrac {{2x + 3} }{ {x + 1}}\) D. \(y = {x^4} - 3{x^2} - 1\). Câu 20. Cho hàm số \(y = {x^4} - 4{x^2} + 3\). Mệnh đề nào dưới đây sai ? A. Hàm số chỉ có một điểm cực trị. B. Đồ thị của hàm số nhận trục tung làm trục đối xứng. C. Hàm số đã cho là hàm số chẵn D. Các điểm cực trị của đồ thị hàm số tạo thành một tam giác cân. Câu 21. Cho hàm số y = f(x) có bảng biến thiên như sau:
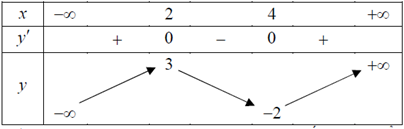
Khẳng định nào sau đây đúng ? A. Hàm số đạt cực đại tại x = 4. B. Hàm số đạt cực tiểu tại x = - 2 . C. Hàm số đạt cực tiểu tại x = 3. D. Hàm số đạt cực đại tại x = 2. Câu 22. Cho đồ thị (C): \(y = {x^4} - 2{x^2}\). Khẳng định nào sau đây là sai ? A. (C) cắt trục Ox tại ba điểm phân biệt. B. (C) cắt trục Oy tại hai điểm phân biệt. C. (C) tiếp xúc với trục Ox. D. (C) nhận Oy làm trục đối xứng. Câu 23. Cho hàm số f(x) có đạo hàm trên R. Nếu hàm số f(x) đồng biến trên R thì A. \(f'(x) \ge 0,\forall x \in R\) B. \(f'(x) = 0,\forall x \in R\) C. \(f'(x) < 0,\forall x \in R\) D.\(f'(x) \le 0,\forall x \in R\) Câu 24. Cho đồ thị (C): \(y = \dfrac{{4x - 1} }{{x + 1}}\). Tọa độ tâm đối xứng của (C) là A. I(- 1 ; 4) B. I(4 ; - 1) C. I(1 ; 4) D. \(I\left( {\dfrac{1}{ 4}; - 1} \right)\) Câu 25. Cho hàm số y = f(x) có đạo hàm trên (a ; b). Nếu f’(x) đổi dấu từ âm sang dương qua điểm x0 thì A. x0 là điểm cực đại của hàm số. B. x0 là điểm cực tiểu của hàm số. C. x0 là điểm cực đại của đồ thị hàm số. D. x0 là điểm cực tiểu của đồ thị hàm số. Lời giải chi tiết
Câu 1. D Đths có TCĐ: \(x = - 1\) nên loại A, C. Đths đi qua điểm \(\left( {0; - 1} \right)\) nên chỉ có D thỏa mãn. Câu 2. C \(y = {x^3} - 3{x^2} + 1\) \(TXD:D = R\) \(\begin{array}{l}y' = 3{x^2} - 6x\\y' = 0 \Leftrightarrow 3{x^2} - 6x = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\end{array}\)
Từ BBT ta có đồ thị hàm số \(y = {x^3} - 3{x^2} + 1\) cắt đường thẳng \(y = m\) tại 3 điểm phân biệt \( \Rightarrow - 3 < m < 1\) Câu 3. A Xét phương trình hoành độ \(\begin{array}{l}x - 1 = \dfrac{{2x - 1}}{{x + 1}},x \ne - 1\\ \Leftrightarrow {x^2} - 1 = 2x - 1 \Leftrightarrow {x^2} - 2x = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\end{array}\) Hoành độ giao điểm của đường thẳng \(y = x - 1\) và \(y = \dfrac{{2x - 1}}{{x + 1}}\) là \(\left( {0, - 1} \right),\left( {2,1} \right)\) Câu 4. D \(TXD:D = R\) \(\begin{array}{l}y = \dfrac{{{x^3}}}{3} - 2{x^2} + 3x - 5\\y' = {x^2} - 4x + 3\\y' = 0 \Leftrightarrow {x^2} - 4x + 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\end{array}\)
Từ BBT xct=3, yct=-5 \(y'\left( 3 \right) = 0\) nên phương trình tiếp tuyến tại \(\left( {3; - 5} \right)\) là: \(y = 0\left( {x + 3} \right) - 5\) hay \(y = - 5\) Đường thẳng này song song với trục hoành. Chọn D. Câu 5. D \(\begin{array}{l}y = \dfrac{{1 - 4x}}{{2x - 1}}(x \ne \dfrac{1}{2})\\\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{1 - 4x}}{{2x - 1}} = - 2\end{array}\) Suy ra TCN y=-2 Câu 6. C Có \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \) nên \(a < 0\), loại B. Đồ thị hàm số đi qua điểm \(\left( {0;1} \right)\) nên chỉ có C thỏa mãn. Câu 7. A Hàm số nghịch biến trên \(\left( {0;1} \right)\) và \(( - \infty ;-1)\) Câu 8. C \(y = {x^3} - 3x + 2\) \(TXD:D = R\) \(\begin{array}{l}y' = 3{x^2} - 3\\y' = 0 \Leftrightarrow 3{x^2} - 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\end{array}\)
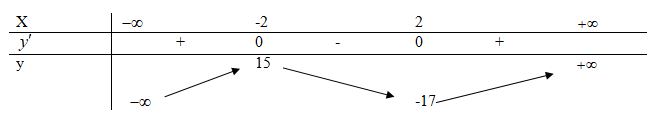
Từ BBT suy ra đồ thị hàm số \(y = {x^3} - 3x + 2\) cắt đường thẳng \(y = m - 1\) tại 3 điểm phân biệt \( \Rightarrow 0 < m - 1 < 4 \Leftrightarrow 1 < m < 5\) Câu 9. B Đáp án A: tâm đối xứng là giao hai đường tiệm cận \(x = - 2\) và \(y = 1\) nên có tọa độ \(\left( { - 2;1} \right)\)( loại). Đáp án B: \(\begin{array}{l}y' = 6{x^2} - 12x + 1\\y'' = 12x - 12 = 0 \Leftrightarrow x = 1\\ \Rightarrow y = {2.1^3} - {6.1^2} + 1 + 1 = - 2\end{array}\) \( \Rightarrow I\left( {1; - 2} \right)\) là tâm đối xứng của đồ thị. Câu 10. A Giá trị cực tiểu của hàm số bằng \(0\) nên A sai. Câu 11. B \(y = \dfrac{3}{{x - 2}}\) TXĐ:\(D = R\backslash {\rm{\{ }}2\} \) \(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} \dfrac{3}{{x - 2}} = + \infty \\\mathop {\lim }\limits_{X \to {2^ - }} \dfrac{3}{{x - 2}} = - \infty \end{array} \right\} \) \(\Rightarrow TCĐ:x = 2\) \(\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{3}{{x - 2}} = 0\) \( \Rightarrow TCN y=0\) Câu 12. D \(y = \dfrac{{1 - 2x}}{{ - x + 2}}\) TXĐ:\(D = R\backslash {\rm{\{ }}2\} \) \(\begin{array}{l}\mathop {\lim }\limits_{X \to \pm \infty } \dfrac{{1 - 2x}}{{ - x + 2}} = 2 \Rightarrow TCN:y = 2\\\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ - }} \dfrac{{1 - 2x}}{{ - x + 2}} = - \infty \\\mathop {\lim }\limits_{x \to {2^ + }} \dfrac{{1 - 2x}}{{ - x + 2}} = + \infty \end{array} \right\} \\\Rightarrow TCĐ:x = 2\end{array}\) Câu 13. C \(y = {x^3} - 3{x^2} + 3x - 4\) \(TXD:D = R\) \(\begin{array}{l}y' = 3{x^2} - 6x + 3\\y' = 0 \Leftrightarrow 3{x^2} - 6x + 3 = 0\\ \Leftrightarrow x = 1\end{array}\)
Hàm số đồng biến trên R nên không có cực trị. Câu 14. D \(y = {x^3} - 12x - 1\) \(TXD:D = R\) \(\begin{array}{l}y' = 3{x^2} - 12\\y' = 0 \Leftrightarrow 3{x^2} - 12 = 0\\ \Leftrightarrow {x^2} - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\end{array}\)
\(\begin{array}{l}{x_{cd}} = - 2 \Rightarrow {y_{cd}} = 15\\{x_{ct}} = 2 \Rightarrow {y_{ct}} = - 17\end{array}\) Câu 15. C Đồ thị hàm đa thức không có đường tiệm cận nên loại A, B. Đáp án C có đường tiệm cận đứng là x=1 nên thỏa mãn. Câu 16. A \(y = \dfrac{{x + 1}}{{x - 1}}\) TXĐ :\(D = R\backslash {\rm{\{ }}1\} \) \(y' = \dfrac{{ - 2}}{{{{\left( {x - 1} \right)}^2}}} < 0\forall x \ne 1\) Hàm nghịch biến trên \(( - \infty ,1)\) và\((1, + \infty )\) Câu 17. C \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 1\) nên \(y = 1\) là đường TCN của đồ thị hàm số \(y = f\left( x \right)\) Câu 18. B \(y = - {x^3} + 3x - 5\) \(TXD:D = R\) \(\begin{array}{l}y' = - 3{x^2} + 3\\y' = 0 \Leftrightarrow - 3{x^2} + 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\end{array}\)
Đồng biến trên \((-1,1) .\) Câu 19. A Đáp án A: \(y' = \cos x - 1 \le 0,\forall x \in \mathbb{R}\) vì \(\cos x \le 1\) với mọi \(x \in \mathbb{R}\) Vậy hàm số \(y = \sin x - x\) luôn nghịch biến trên \(\mathbb{R}\) Câu 20. A Ta có: \(y' = 4{x^3} - 8x = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \end{array} \right.\) Do đó hàm số có 3 điểm cực trị nên A sai. Câu 21. D Hàm số đạt cực tiểu tại x=4, đạt cực đại tại x=2 nên chỉ có D đúng. Câu 22. B Cho x=0 thì y=0 nên đồ thị hàm số chỉ cắt trục Oy tại 1 điểm duy nhất. Câu 23. A Nếu hàm số f(x) đồng biến trên R thì f'(x) \(\ge 0\) trên R. Câu 24. A \(y = \dfrac{{4x - 1}}{{x + 1}}\) TXĐ: D=R\{1} \(\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{4x - 1}}{{x + 1}} = 4\) nên TCN: y=4 \(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {{( - 1)}^ + }} \dfrac{{4x - 1}}{{x + 1}} = + \infty \\\mathop {\lim }\limits_{x \to {{( - 1)}^ - }} \dfrac{{4x - 1}}{{x + 1}} = - \infty \end{array} \right\} \)\(\,\Rightarrow TCĐ: x= -1\) \( \Rightarrow \) tâm đối xứng I(-1,4) Câu 25. B Nếu f’(x) đổi dấu từ âm sang dương qua điểm x0 thì x0 là điểm cực tiểu của hàm số. HocTot.XYZ
|