Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Đề số 2 - Hình học 10Đáp án và lời giải chi tiết Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Đề số 2 - Hình học 10 Đề bài Câu 1 (2đ) Cho hình chữ nhật ABCD, \(AB = 3;AD = 4\) Hãy tính? a. \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|\) b. \(\left| {2\overrightarrow {AB} + 3\overrightarrow {AD} } \right|\) Câu 2 (1đ) Cho \(\Delta ABC\) có đường trung tuyến AM. Gọi I là trung điểm của AM. Chứng minh các đẳng thức vectơ sau: a) \(\overrightarrow {AB} + \overrightarrow {CI} = \overrightarrow {AI} + \overrightarrow {CB} \) b) \(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \) Câu 3 (2đ) Cho các véc tơ : \(\overrightarrow a = (2; - 3)\) , \(\overrightarrow b = ( - 5;1)\) và \(\overrightarrow c = ( - 5; - 12)\). a) Tính toạ độ véc tơ \(\overrightarrow u = \overrightarrow {2a} + 3\overrightarrow b \) . b) Phân tích vectơ \(\overrightarrow c \) theo hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \). Câu 4 (2.5đ) Trong mặt phẳng tọa độ Oxy, cho ba điểm A(4;1); B(0;3); C(1;2). a) Chứng minh ba điểm A, B, C lập thành ba đỉnh của một tam giác. b) Tìm tọa độ của trung điểm cạnh AB. c) Tìm tọa độ trọng tâm G của tam giác ABC. d) Tìm tọa độ điểm D của hình bình hành ABCD. e) Tìm tọa độ điểm E thuộc trục hoành sao cho \(AE + BE\) đạt giá trị nhỏ nhất. Câu 5 (1đ) Cho hình bình hành ABCD. Gọi M là trung điểm của AB. a. Tính \(\overrightarrow {DM} \) theo \(\overrightarrow {DA} \) và \(\overrightarrow {DC} \); b. Gọi N là điểm thỏa mãn \(\overrightarrow {NC} + 2\overrightarrow {NA} = \overrightarrow 0 \). Chứng minh D, N, M thẳng hàng. Câu 6 (0.75đ) Cho tam giác ABC.Tìm tập hợp các điểm M thỏa mãn \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \dfrac{3}{2}\left| {\overrightarrow {MB} + \overrightarrow {MC} } \right|\) Câu 7 (0.75đ) Biết tháp Eiffel ở thủ đô Paris nước Pháp có chiều cao là 324m. Khi xây dựng người ta thiết kế theo tỉ lệ vàng. Tính độ cao từ mặt đất tới tầng 2 của tháp (Đoạn AB)
Lời giải chi tiết Câu 1 (2 điểm)
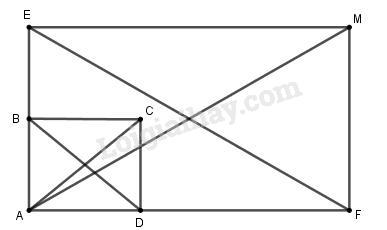
a) Ta có: ABCD là hình chữ nhật nên \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC\) Tam giác ABC vuông tại B nên theo Pitago ta có: \(AC = \sqrt {A{B^2} + B{C^2}} \) \( = \sqrt {{3^2} + {4^2}} = 5\) Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = 5\). b) Dựng các điểm E, F sao cho \(\overrightarrow {AE} = 2\overrightarrow {AB} ;\overrightarrow {AF} = 3\overrightarrow {AD} \) \(\begin{array}{l} \Rightarrow AE = 2AB = 2.3 = 6\\AF = 3AD = 3.4 = 12\end{array}\) Dựng hình chữ nhật \(AEMF\) ta có : \(\left| {2\overrightarrow {AB} + 3\overrightarrow {AD} } \right| = \left| {\overrightarrow {AE} + \overrightarrow {AF} } \right|\)\( = \left| {\overrightarrow {AM} } \right| = AM\) Tam giác \(AEM\) vuông tại E nên theo Pitago ta có: \(AM = \sqrt {A{E^2} + E{M^2}} \)\( = \sqrt {{6^2} + {{12}^2}} = 6\sqrt 5 \) Câu 2 (1 điểm)
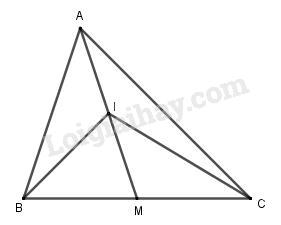
a. \(\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CI} = \overrightarrow {AI} + \overrightarrow {CB} \\ \Leftrightarrow \left( {\overrightarrow {AB} - \overrightarrow {AI} } \right) + \overrightarrow {CI} - \overrightarrow {CB} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {CI} + \overrightarrow {IB} - \overrightarrow {CB} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {CB} - \overrightarrow {CB} = \overrightarrow 0 \end{array}\) b. \(2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \)\( \Leftrightarrow 2\overrightarrow {IA} + 2\overrightarrow {IM} = \overrightarrow 0 \) \( \Leftrightarrow 2\left( {\overrightarrow {IA} + \overrightarrow {IM} } \right) = \overrightarrow 0 \) (đúng vì I là trung điểm của AM) (đpcm) Câu 3 (2 điểm) \(\overrightarrow a = (2; - 3)\) , \(\overrightarrow b = ( - 5;1)\) và \(\overrightarrow c = ( - 5; - 12)\) a. \(\begin{array}{l}2\overrightarrow a = (4; - 6)\\3\overrightarrow b = ( - 15;3)\end{array}\) \(\overrightarrow u = \overrightarrow {2a} + 3\overrightarrow b = \left( { - 11; - 3} \right)\) b. Gọi hai số m, n thoã mãn \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b \) Ta có hệ phương trình :\(\left\{ \begin{array}{l}2m - 5n = - 5\\ - 3m + n = - 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 5\\n = 3\end{array} \right.\) Vậy : \(\overrightarrow c = 5\overrightarrow a + 3\overrightarrow b \) Câu 4 (2.5 điểm) A(4;1); B(0;3); C(1;2). a. \(\overrightarrow {AB} = \left( { - 4;2} \right);\overrightarrow {AC} = \left( { - 3;1} \right)\) Ta có \(\dfrac{{ - 4}}{{ - 3}} \ne \dfrac{2}{1}\) nên \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương. Vậy A, B, C là 3 đỉnh của tam giác. b. Gọi \(M\) là trung điểm của \(AB\) thì \(\left\{ \begin{array}{l}{x_M} = \dfrac{{{x_A} + {x_B}}}{2} = \dfrac{{4 + 0}}{2} = 2\\{y_M} = \dfrac{{{y_A} + {y_B}}}{2} = \dfrac{{1 + 3}}{2} = 2\end{array} \right.\) \( \Rightarrow M\left( {2;2} \right)\) Vậy tọa độ trung điểm của AB là :\(M\left( {2;2} \right)\) c. Gọi \(G\) là trọng tâm tam giác \(ABC\) thì: \(\left\{ \begin{array}{l}{x_G} = \dfrac{{4 + 0 + 1}}{3} = \dfrac{5}{3}\\{y_G} = \dfrac{{1 + 3 + 2}}{3} = 2\end{array} \right.\) \( \Rightarrow G\left( {\dfrac{5}{3};2} \right)\) Vậy tọa độ trọng tâm G của tam giác ABC: \(G\left( {\dfrac{5}{3};2} \right)\) d. \(\overrightarrow {BC} = \left( {1; - 1} \right)\) ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AD} = \overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}{x_D} - 4 = 1\\{y_D} - 1 = - 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 5\\{y_D} = 0\end{array} \right.\) Vậy \(D\left( {5;0} \right)\) e.
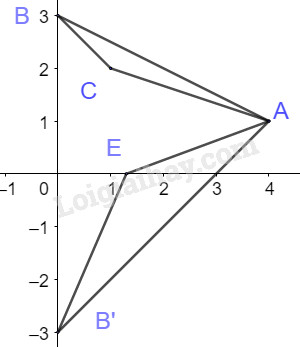
Gọi \(E\left( {{x_E};0} \right) \in Ox\) Gọi B’ đối xứng với B qua trục Ox thì \(B'\left( {0; - 3} \right)\) \(AE + BE = AE + B'E \ge AB'\) Do đó \(AE + BE\) đạt GTNN bằng \(AB'\) khi A,B’,E thẳng hàng \( \Leftrightarrow \overrightarrow {AE} = k\overrightarrow {AB'} \)\( \Leftrightarrow \left\{ \begin{array}{l}{x_E} - 4 = - 4k\\0 - 1 = k.\left( { - 4} \right)\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}k = \dfrac{1}{4}\\{x_E} = 3\end{array} \right.\) Vậy \(E\left( {3;0} \right)\) Câu 5 (1 điểm)
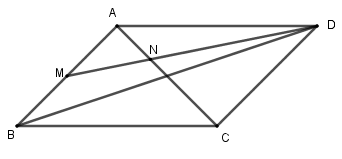
a. \(\overrightarrow {DM} = \dfrac{1}{2}\left( {\overrightarrow {DA} + \overrightarrow {DB} } \right)\)\( = \dfrac{1}{2}\left( {\overrightarrow {DA} + \overrightarrow {DA} + \overrightarrow {DC} } \right)\) \( = \dfrac{1}{2}\left( {2\overrightarrow {DA} + \overrightarrow {DC} } \right) = \overrightarrow {DA} + \dfrac{1}{2}\overrightarrow {DC} \) (1) b. \(\overrightarrow {NC} + 2\overrightarrow {NA} = \overrightarrow 0 \) \(\begin{array}{l} \Leftrightarrow \overrightarrow {DC} - \overrightarrow {DN} + 2\left( {\overrightarrow {DA} - \overrightarrow {DN} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {DC} - \overrightarrow {DN} + 2\overrightarrow {DA} - 2\overrightarrow {DN} = \overrightarrow 0 \\ \Leftrightarrow 3\overrightarrow {DN} = 2\overrightarrow {DA} + \overrightarrow {DC} \\ \Leftrightarrow \dfrac{3}{2}\overrightarrow {DN} = \overrightarrow {DA} + \dfrac{1}{2}\overrightarrow {DC} \,\,\,\,\,\,\left( 2 \right)\end{array}\) Từ (1) và (2) suy ra: \(\overrightarrow {DM} = \dfrac{3}{2}\overrightarrow {DN} \) nên 3 điểm D, M, N thẳng hàng. Câu 6 (0.75 điểm) Gọi G là trọng tâm tam giác ABC, I là trung điểm BC. Khi đó \(\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \\\overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MI} \end{array}\) \(\begin{array}{l}\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \dfrac{3}{2}\left| {\overrightarrow {MB} + \overrightarrow {MC} } \right|\\ \Leftrightarrow \left| {3\overrightarrow {MG} } \right| = \dfrac{3}{2}\left| {2\overrightarrow {MI} } \right|\\ \Leftrightarrow 3\left| {\overrightarrow {MG} } \right| = 3\left| {\overrightarrow {MI} } \right|\\ \Leftrightarrow MG = MI\end{array}\) Vậy tập hợp các điểm M là đường trung trực của đoạn GI. Câu 7 (0.75 điểm) Do xây theo tỉ lệ vàng nên ta có \(\dfrac{{BC}}{{AB}} = 1,618 \Rightarrow BC = 1,618AB\) Mà \(BC + AB = 324\) nên \(1,618AB + AB = 324\) \( \Leftrightarrow 2,618AB = 324\) \( \Leftrightarrow AB = 123,76\) Vậy độ cao của tháp là \(123,76\left( m \right)\). Sưu tầm HocTot.XYZ
|