Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Hình học 10Đáp án và lời giải chi tiết Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Hình học 10 Đề bài A. Trắc nghiệm: Câu 1: Cho G là trọng tâm \(\Delta \)ABC, O là điểm bất kỳ thì ta có: A. \(\overrightarrow {AG} = \dfrac{{\overrightarrow {OB} + \overrightarrow {OC} }}{2}\) B. \(\overrightarrow {AG} = \dfrac{{\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {AC} }}{3}\) C. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \) D. \(\overrightarrow {AG} = \dfrac{2}{3}(\overrightarrow {AB} + \overrightarrow {AC} )\) Câu 2: Chọn mệnh đề đúng : A. Hai vectơ không cùng hướng thì luôn ngược hướng B. Hai vectơ có độ dài bằng nhau thì bằng nhau C. Hai vectơ cùng phương thì cùng hướng D. Hai vectơ bằng nhau thì cùng hướng Câu 3: Cho \(\Delta ABC\) cân ở A, đường cao AH, câu nào sau đây đúng: A. \(\overrightarrow {HB} = \overrightarrow {HC} \) B. \(\overrightarrow {AB} = \overrightarrow {AC} \) C. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right|\) D. Tất cả các đáp án trên đều sai Câu 4: Cho ∆ ABC vuông cân tại A, H là trung điểm BC, đẳng thức nào sau đây là đúng ? A. \(\;\overrightarrow {AB} = \overrightarrow {AC} \;\) B. \(\overrightarrow {BC} = 2\overrightarrow {CH} \) C. \(\;\overrightarrow {BC} = 2\overrightarrow {AH} \) D. \(\overrightarrow {BH} = \overrightarrow {HC} \) Câu 5: Cho tam giác ABC có G là trọng tâm, M là trung điểm của BC, đẳng thức nào sau đây là đúng ? A. \(\overrightarrow {MG} = - \dfrac{1}{3}\overrightarrow {MA} \) B. \(\overrightarrow {GA} = 2\overrightarrow {GM} \) C. \(\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} \) D. \(\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GM} \) Câu 6: Cho \(\Delta ABC\) với M là trung điểm của BC, đẳng thức nào sau đây là đúng ? A. \(\,\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AM} \) B.\(\,\,\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \) C. \(\,\,\overrightarrow {AM} + \overrightarrow {MB} + \overrightarrow {AB} = \overrightarrow 0 \) D. \(\,\,\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {2MA} \,\,\,\) Câu 7: Cho 4 điểm A, B, C, D bất kỳ, chọn đẳng thức đúng: A. \(\overrightarrow {BA} - \overrightarrow {CA} - \overrightarrow {DC} = \overrightarrow {BD} \) B. \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {BD} \) C. \(\overrightarrow {CB} + \overrightarrow {BA} + \overrightarrow {AD} = \overrightarrow {DC} \) D. \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \) Câu 8: Cho lục giác đều ABCDEF có tâm O. Số các véctơ khác véctơ không, ngược hướng với \(\overrightarrow {OA} \), có điểm đầu và điểm cuối là đỉnh của lục giác là: A. 2 B. 4 C. 6 D. 3 Câu 9: Xác định vị trí 3 điểm A, B, C thỏa hệ thức: \(\overrightarrow {AB} = \overrightarrow {CA} \) là: A. A là trung điểm của BC B. \(\Delta \)ABC cân C. A, B, C thẳng hàng D. C trùng B Câu 10: Cho hình chữ nhật ABCD, đẳng thức nào sau đây là đúng ? A. \(\overrightarrow {AB} + \overrightarrow {DB} = \overrightarrow {AD} \) B. \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {BC} \) C. \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {CA} \) D. \(\;\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right|\) B. Tự luận: Câu 1: Cho hình bình hành ABCD có tâm O. a. Chứng minh rằng : \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} - \overrightarrow {BC} \). b. Phân tích \(\overrightarrow {OA} \) theo \(\overrightarrow {AB} ,\overrightarrow {AD} \). Câu 2: Cho tam giác ABC, gọi O, H, G lần lượt là tâm đường tròn ngoại tiếp, trực tâm, trọng tâm của tam giác ABC a. Chứng minh rằng: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \) b. Chứng minh ba điểm O, H, G thẳng hàng. Lời giải chi tiết Phần I: Trắc nghiệm (5đ)
Câu 1: Cách giải: G là trọng tâm tam giác, với điểm O bất kì thì \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \) Chọn C Câu 2: Cách giải: Đáp án A: sai vì có thể hai véc tơ đó không cùng phương nên sẽ không ngược hướng được. Đáp án B: sai vì hai véc tơ này có thể sẽ không cùng hướng. Đáp án C: sai vì có thể ngược hướng. Chọn D Câu 3: Cách giải:
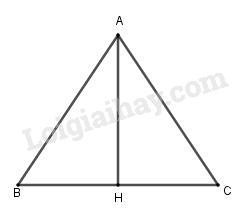
Đáp án A: sai vì \(\overrightarrow {HA} = - \overrightarrow {HB} \) Đáp án C: đúng vì \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right| = AB = AC\). Đáp án B: sai vì hai véc tơ này không cùng hướng. Chọn C Câu 4: Cách giải:
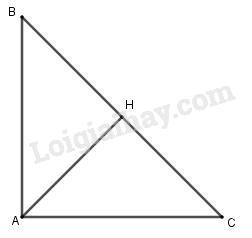
Đáp án A: sai vì hai véc tơ này không cùng hướng. Đáp án B: sai vì \(\overrightarrow {BC} = - 2\overrightarrow {CH} \) Đáp án C: sai vì \(\overrightarrow {BC} ,\overrightarrow {AH} \) không cùng hướng. Chọn D Câu 5: Cách giải:
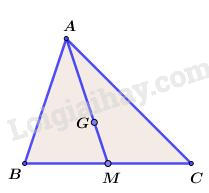
Đáp án A sai vì \(\overrightarrow {MG} = \dfrac{1}{3}\overrightarrow {MA} \) Đáp án B sai vì \(\overrightarrow {GA} = - 2\overrightarrow {GM} \) Đáp án C sai vì \(\overrightarrow {GB} + \overrightarrow {GC} = - \overrightarrow {GA} \) (do \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)) Chọn D Câu 6: Cách giải: Đáp án A và D sai vì \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \). Đáp án C sai vì \(\overrightarrow {AM} + \overrightarrow {MB} + \overrightarrow {AB} = \overrightarrow {AB} + \overrightarrow {AB} = 2\overrightarrow {AB} \ne \overrightarrow 0 \). Đáp án B đúng. Chọn B Câu 7: Cách giải: Đáp án A: \(\begin{array}{l}\overrightarrow {BA} - \overrightarrow {CA} - \overrightarrow {DC} \\ = \overrightarrow {BA} + \overrightarrow {AC} + \overrightarrow {CD} \\ = \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {BD} \end{array}\) Nên A đúng. Chọn A Câu 8: Cách giải:
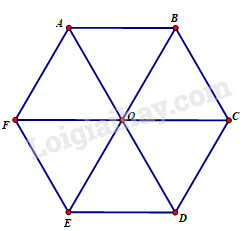
Các véc tơ khác \(\overrightarrow 0 \), ngược hướng \(\overrightarrow {OA} \) và có điểm đầu, điểm cuối là đỉnh của lục giác là: \(\overrightarrow {AD} ,\overrightarrow {BC} ,\overrightarrow {FE} \) Chọn D Câu 9: Cách giải: \(\begin{array}{l}\overrightarrow {AB} = \overrightarrow {CA} \Leftrightarrow \overrightarrow {AB} - \overrightarrow {CA} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow 0 \end{array}\) Vậy A là trung điểm của BC. Chọn A Câu 10: Cách giải: Ta có: \(\begin{array}{l}\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC\\\left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB\end{array}\) Mà ABCD là hình chữ nhật nên \(AC = DB\) hay \(\;\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right|\) Chọn D Phần II: Tự luận (5đ) Câu 1: Cách giải:
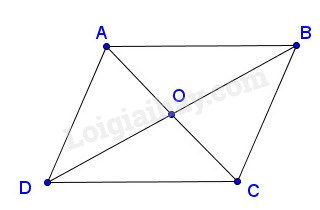
a) ABCD là hình bình hành nên \(\overrightarrow {AB} = - \overrightarrow {CD} \Rightarrow \overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow 0 \) \(\overrightarrow {AD} = \overrightarrow {BC} \Rightarrow \overrightarrow {AD} - \overrightarrow {BC} = \overrightarrow 0 \) Vậy \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} - \overrightarrow {BC} \left( { = \overrightarrow 0 } \right)\) b) Ta có: O là trung điểm của BD nên \(\begin{array}{l}\overrightarrow {AB} + \overrightarrow {AD} = 2\overrightarrow {AO} \\ \Rightarrow \overrightarrow {AO} = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\\ \Rightarrow - \overrightarrow {OA} = \dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {AD} \\ \Rightarrow \overrightarrow {OA} = - \dfrac{1}{2}\overrightarrow {AB} - \dfrac{1}{2}\overrightarrow {AD} \end{array}\) Câu 2: Cách giải: a) G là trọng tâm của tam giác ABC nên: \(\begin{array}{l}\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \\ \Rightarrow \overrightarrow {GO} + \overrightarrow {OA} + \overrightarrow {GO} + \overrightarrow {OB} + \overrightarrow {GO} + \overrightarrow {OC} = \overrightarrow 0 \\ \Leftrightarrow 3\overrightarrow {GO} + \left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = - 3\overrightarrow {GO} \\ \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \end{array}\) Cách khác: Ta có: \(\begin{array}{l}\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \\ = \overrightarrow {OG} + \overrightarrow {GA} + \overrightarrow {OG} + \overrightarrow {GB} + \overrightarrow {OG} + \overrightarrow {GC} \\ = 3\overrightarrow {OG} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right)\\ = 3\overrightarrow {OG} + \overrightarrow 0 \\ = 3\overrightarrow {OG} \end{array}\)
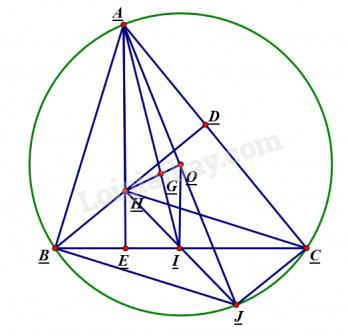
b) Kẻ đường kính \(AJ\). Ta có: \(\left\{ \begin{array}{l}BH \bot AC\\JC \bot AC\end{array} \right. \Rightarrow BH//JC\) \(\left\{ \begin{array}{l}CH \bot AB\\JB \bot AB\end{array} \right. \Rightarrow CH//JB\) Do đó BHCJ là hình bình hành Gọi I là trung điểm của BC thì I là trung điểm của HJ. Tam giác AHJ có OI là đường trung bình nên \(\overrightarrow {OI} = \dfrac{1}{2}\overrightarrow {AH} \Rightarrow \overrightarrow {AH} = 2\overrightarrow {OI} \) Mà \(\overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {OI} \) nên \(\begin{array}{l}\overrightarrow {AH} = \overrightarrow {OB} + \overrightarrow {OC} \\ \Leftrightarrow \overrightarrow {OH} - \overrightarrow {OA} = \overrightarrow {OB} + \overrightarrow {OC} \\ \Leftrightarrow \overrightarrow {OH} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \\ \Rightarrow \overrightarrow {OH} = 3\overrightarrow {OG} \end{array}\) Vậy ba điểm O, H, G thẳng hàng. HocTot.XYZ
|