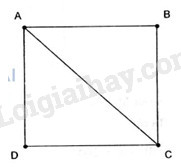
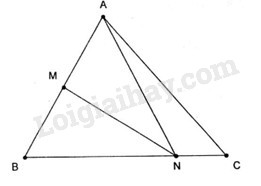
Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Hình học 10Đáp án và lời giải chi tiết Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Hình học 10 Đề bài Câu 1.Cho hình vuông ABCD cạnh bằng a, M là điểm bất kì. a.Chứng minh véc tơ \(\overrightarrow v = 4\overrightarrow {MA} - \overrightarrow {MB} - 2\overrightarrow {MC} - \overrightarrow {MD} \) không phụ thuộc vào M. b.Tính độ dài của \(\overrightarrow v \) . Câu 2.Cho tam giác ABC có M là trung điểm AB và N là điểm trên đoạn BC sao cho BN= 3NC. a. Chứng minh rằng \(\overrightarrow {AN} = \dfrac{1 }{4}\overrightarrow {AB} + \dfrac{3 }{4}\overrightarrow {AC} \) . b. Hãy biểu thị véc tơ \(\overrightarrow {MN} \) theo các véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) . Câu 3. Cho tam giác ABC. Tìm tập hợp điểm M sao cho \(\left| {2\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)} \right|\)\( = \left| {3\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right)} \right|\) . Câu 4. Trong mặt phẳng tọa độ Oxy cho hai điểm A(-4;3) và B(2;-5). a. Tìm tọa độ điểm A’ đối xứng với A qua B. b. Tìm tọa độ điểm M thuộc trục hoành sao cho A, B, M thẳng hàng. Lời giải chi tiết Câu 1. a.Ta có \(\overrightarrow v = 4\overrightarrow {MA} - \overrightarrow {MB} - 2\overrightarrow {MC} - \overrightarrow {MD} \) \( = \left( {\overrightarrow {MA} - \overrightarrow {MB} } \right) + \left( {2\overrightarrow {MA} - 2\overrightarrow {MC} } \right) \)\(+ \left( {\overrightarrow {MA} - \overrightarrow {MD} } \right)\) \(= \overrightarrow {BA} + 2\overrightarrow {CA} + \overrightarrow {DA} \) \( = - \overrightarrow {AB} - 2\overrightarrow {AC} - \overrightarrow {AD} \) \(= - \left( {\overrightarrow {AB} + \overrightarrow {AD} + 2\overrightarrow {AC} } \right)\) \( = - \left( {\overrightarrow {AC} + 2\overrightarrow {AC} } \right) = - 3\overrightarrow {AC} \) \(= 3\overrightarrow {CA} \) Vậy \(\overrightarrow v \) không phụ thuộc vào M. b. Tam giác ABC vuông tại B nên theo Pitago ta có: \(AC = \sqrt {A{B^2} + B{C^2}} \)\( = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \) \(\left| {\overrightarrow v } \right| = \left| {3\overrightarrow {CA} } \right| \)\(= 3CA = 3a\sqrt 2 \) Câu 2.
a.Ta có: \(\overrightarrow {NB} = - 3\overrightarrow {NC} \) \(\Leftrightarrow \overrightarrow {AB} - \overrightarrow {AN} = - 3\left( {\overrightarrow {AC} - \overrightarrow {AN} } \right)\) \(\begin{array}{l} \( \Leftrightarrow 4\overrightarrow {AN} = \overrightarrow {AB} + 3\overrightarrow {AC}\) \( \Leftrightarrow \overrightarrow {AN} = \dfrac{1}{ 4}\overrightarrow {AB} + \dfrac{3 }{4}\overrightarrow {AC} \) b.Ta có \(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} \) \(= \dfrac{1 }{ 4}\overrightarrow {AB} + \dfrac{3 }{ 4}\overrightarrow {AC} - \dfrac{1 }{ 2}\overrightarrow {AB} \) \(= - \dfrac{1 }{ 4}\overrightarrow {AB} + \dfrac{3 }{ 4}\overrightarrow {AC} \) Câu 3.
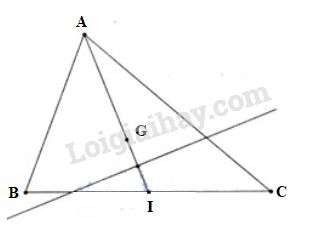
Gọi G là trọng tâm tam giác ABC, I là trung điểm BC. Ta có: \(\left| {2\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)} \right| \)\(= \left| {3\left( {\overrightarrow {MB} + \overrightarrow {MC} } \right)} \right|\) \(\Leftrightarrow \left| {6\overrightarrow {MG} } \right| = \left| {6\overrightarrow {MI} } \right| \Leftrightarrow MG = MI\) M cách đều hai điểm cố định G và I nên tập hợp các điểm M là đường trung trực của đoạn GI. Câu 4. a. \(A(-4;3)\) và \(B(2;-5).\) \(A'\) đối xứng với A qua B khi và chỉ khi B là trung điểm của đoạn \({\rm{AA'}}\) . Do đó \(\left\{ \matrix{ {x_B} = \dfrac{{{x_A} + {x_{A'}}}}{2}\hfill \cr {y_B} = \dfrac{{{y_A} + {y_{A'}}}}{2} \hfill \cr} \right. \) \(\Leftrightarrow \left\{ \matrix{ {x_{A'}} = 2{x_B} - {x_A} = 8 \hfill \cr {y_{A'}} = 2{y_B} - {y_A} = - 13 \hfill \cr} \right.\) Vậy \(A' = \left( {8; - 13} \right)\) . b.Gọi \(M\left( {{x_M};0} \right)\) là điểm trên trục hoành. Ta có \(\overrightarrow {AM} = \left( {{x_M} + 4; - 3} \right),{\rm{ }}\overrightarrow {AB} = \left( {6; - 8} \right)\) . M, A, B thẳng hàng khi và chỉ khi \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng phương \(\dfrac{{{x_M} + 4}}{6} = \dfrac{{ - 3}}{{ - 8}} \) \(\Leftrightarrow 4{x_M} + 16 = 9\) \(\Leftrightarrow {x_M} = - \dfrac{7}{4}\) Vậy \(M = \left( { - \dfrac {7 }{ 4};0} \right)\) . HocTot.XYZ
|