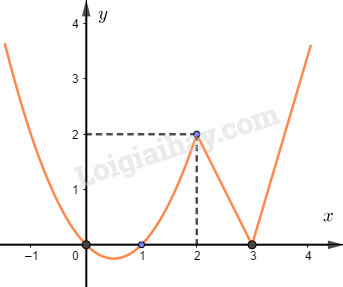
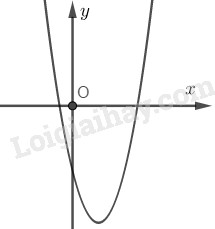
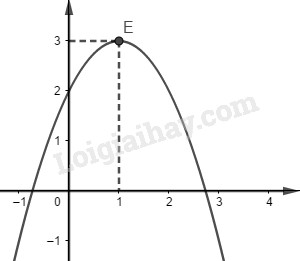
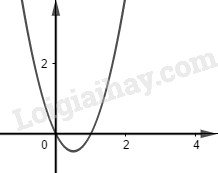
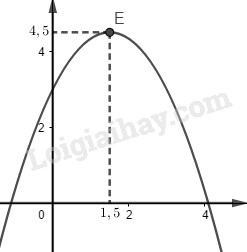
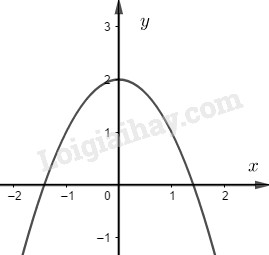
Đề kiểm tra giữa kì 1 Toán 10 đề số 5 có lời giải chi tiếtTổng hợp đề kiểm tra giữa kì 1 có lời giải chi tiết được sưu tầm từ các trường bám sát cấu trúc chương trình học của các em giúp các em ôn tập hiệu quả chuẩn bị cho bài kiểm tra trên lớp Đề bài Câu 1. Cho hai vec tơ \(\overrightarrow a = \left( {3; - 1} \right),\overrightarrow b = \left( {1;0} \right)\). Khẳng định nào sau đây đúng? A. \(\overrightarrow b - \overrightarrow a = \left( {2; - 1} \right)\) B. \(\overrightarrow b - \overrightarrow a = \left( { - 2;1} \right)\) C. \(\overrightarrow a - \overrightarrow b = \left( {4; - 1} \right)\) D. \(\overrightarrow a - \overrightarrow b = \left( {2;1} \right)\) Câu 2. Hai vec tơ \(\overrightarrow a ,\overrightarrow b \) bằng nhau nếu A. Chúng cùng hướng B. Chúng cùng hướng và cùng độ dài C. Chúng cùng phương và cùng độ dài D. Chúng cùng phương. Câu 3. Trong các hàm số sau, hàm số nào là hàm số bậc nhất? A. \(y = \left| x \right| + 1\) B. \(y = {2^{2020}}x - 5\) C. \(y = \dfrac{1}{x}\) D. \(y = {x^3} - 2x\) Câu 4. Tập xác định của hàm số \(y = \dfrac{{2 - x}}{{{x^2} - 3}} + \dfrac{3}{{\sqrt {x + 4} }}\) là A. \(\left( { - 4; - \sqrt 3 } \right) \cup \left( { - \sqrt 3 ;\sqrt 3 } \right) \cup \left( {\sqrt 3 ; + \infty } \right)\) B. \(\left[ { - 4; - \sqrt 3 } \right) \cup \left( { - \sqrt 3 ;\sqrt 3 } \right) \cup \left( {\sqrt 3 ; + \infty } \right)\) C. \(\left[ { - 4; + \infty } \right)\) D. \(\left( { - 4; + \infty } \right)\) Câu 5. Cho hai tập hợp \(A = \left\{ {0;2;4;5;6} \right\},B = \left\{ {1;2;3;4} \right\}\). Khẳng định nào sau đây đúng? A. \(B\backslash A = \left\{ {1;3} \right\}\) B. \(A \cap B = \left\{ 2 \right\}\) C. \(A \cup B = \left\{ {0;1;2;3;5;6} \right\}\) D. \(A\backslash B = \left\{ {0;1;5;6} \right\}\) Câu 6. Cho đồ thị của hàm số \(y = f\left( x \right)\) Hàm số \(y = f\left( x \right)\) đồng biến trên A. \(\left( {2; + \infty } \right)\) B. \(\left( { - \infty ;0} \right)\) C. \(\left( {1;\dfrac{3}{2}} \right)\) D. \(\left( {1;3} \right)\) Câu 7. Cho ba điểm \(A,B,C\) thẳng hàng, trong đó điểm A nằm giữa hai điểm B và C. Khi đó các cặp vectơ nào sau đây cùng hướng? A. \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) B. \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) C. \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \) D. \(\overrightarrow {BC} \) và \(\overrightarrow {CA} \) Câu 8. Có bao nhiêu hàm số chẵn trong các hàm số sau: (1) \(y = \sqrt {x + 1} + \sqrt {1 - x} \); (2) \(y = {x^3} - x\); (3) \(y = {x^2} + 1\); (4) \(y = - 2x + 1\). A. 4 B. 1 C. 3 D. 2 Câu 9. Số tập con của tập hợp \(A = \left\{ {x \in \mathbb{Z}\left| { - \dfrac{7}{4} \le x \le \dfrac{{19}}{{11}}} \right.} \right\}\) A. 8 B. 32 C. 16 D. 4 Câu 10. Cho điểm \(M\left( {1;2} \right)\). Khẳng định nào sau đây sai? A. \({M_1}\left( { - 1;2} \right)\) đối xứng \(M\) qua \(Ox\) B. \({M_2}\left( {1; - 2} \right)\) đối xứng \(M\) qua \(Oy\) C. \({M_4}\left( { - 1;2} \right)\) đối xứng \(M\) qua gốc tọa độ. D. \({M_3}\left( { - 1; - 2} \right)\) đối xứng \(M\) qua gốc tọa độ. Câu 11. Giải phương trình \( - {x^4} + 2{x^2} + 3 = 0\) A. \(x = \sqrt 3 \) B. \(x = - \sqrt 3 \) C. \(x = 1\) D. \(x = \sqrt 3 \) hoặc \(x = - \sqrt 3 \) Câu 12. Giao điểm của đường thẳng \(y = - x + 1\) và parabol \(\left( P \right):y = 4{x^2} - 5x + 2\) là A. \(M\left( {\dfrac{1}{2};\dfrac{1}{2}} \right)\) B. \(M\left( { - \dfrac{1}{2};\dfrac{3}{2}} \right)\) C. \(M\left( {\dfrac{1}{4};\dfrac{3}{4}} \right)\) D. \(M\left( { - 1; - 2} \right)\) Câu 13. Hàm số \(y = 2a{x^2} - bx + 3\) có đỉnh \(I\left( {1;0} \right)\) và đi qua điểm \(A\left( { - 1; - 2} \right)\). Tổng \(S = {a^2} + {b^2}\) bằng A. 2 B. 3 C. 4 D. 5 Câu 14. Cho các phương trình: \({x^2} - 1 = 0\)(1); \({x^2} - 9 = 0\)(2); \({x^2} - 4x + 3 = 0\)(3); \({x^2} - 3x = 0\)(4). Có bao nhiêu phương trình là phương trình hệ quả của phương trình \(\sqrt {2x + 1} = x - 2\) A. 1 B. 2 C. 3 D. 4 Câu 15. Tịnh tiến đồ thị hàm số \(y = \left| {2x + 3} \right| - x + 1\) lên trên 2 đơn vị rồi sang trái 3 đơn vị ta được đồ thị của hàm số nào? A. \(y = 2\left| {x + 3} \right| - x - 2\) B. \(y = \left| {2x + 9} \right| - x\) C. \(y = \left| {2x + 9} \right| - x - 2\) D. \(y = \left| {2x + 3} \right| - x + 3\) Câu 16. Cho hình chữ nhật ABCD có AB=2AD=2a. Gọi M là điểm thuộc đường thẳng AB sao cho \(\overrightarrow {AM} = - \dfrac{1}{4}\overrightarrow {AB} \). Khi đó A. \(\overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \) B. \(\overrightarrow {MC} = \dfrac{1}{5}\overrightarrow {MB} + \overrightarrow {MD} \) C. \(\overrightarrow {MC} = - \dfrac{1}{5}\overrightarrow {MB} + \overrightarrow {MD} \) D. \(\overrightarrow {MC} = \dfrac{4}{5}\overrightarrow {MB} + \overrightarrow {MD} \) Câu 17. Giao điểm của đồ thị hai hàm số \(\left( P \right):y = 2{x^2} + 5x - 2\) và \(\left( {P'} \right):y = {x^2} + 4\) là A. \(A\left( {1;5} \right);B\left( { - 6;40} \right)\) B. \(A\left( { - 1;5} \right);B\left( {6;40} \right)\) C. \(A\left( {2;8} \right);B\left( { - 3;13} \right)\) D. \(A\left( { - 2;8} \right);B\left( {3;13} \right)\) Câu 18. Tìm m để hàm số \(y = - {x^2} + mx + 3 - m\) có giá trị lớn nhất trên \(\mathbb{R}\) bằng 3. A. \(m = 1\) hoặc \(m = 4\) B. \(m = 0\) hoặc \(m = 1\) C. \(m = 0\) hoặc \(m = 4\) D. không tồn tại giá trị của m. Câu 19. Cho hàm số có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?
A. \(a > 0,b < 0,c < 0\) B. \(a > 0,b > 0,c > 0\) C. \(a < 0,b < 0,c < 0\) D. \(a > 0,b > 0,c < 0\) Câu 20. Đồ thị nào dưới đây là đồ thị của hàm số \(y = - {x^2} + 2x + 2\)? A. B.
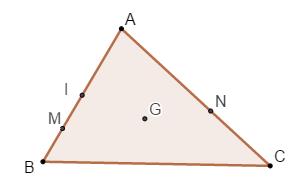
C. D. Câu 21. Tìm m để phương trình \(2mx + 3 = 3{m^2} - 2x\) nghiệm đúng \(\forall x \in \mathbb{R}\). A. \(m = 1\) B. \(m = 1\) và \(m = - 1\) C. \(m = - 1\) D. \(m = 2\) Câu 22. Một người vay ngân hàng 50 000 000 đồng với lãi suất ngân hàng là 4,8% một năm và theo thể thức lãi đơn (tiền lãi không gộp vào chung với tiền gốc). Sau 5 năm người đó nợ ngân hàng bao nhiêu tiền? A. 12 000 000 đồng B. 62 000 000 đồng C. 50 000 000 đồng D. 52 000 000 đồng Câu 23. Tìm m để đồ thị hàm số \(y = 3m\) cắt parabol\(\left( P \right):y = \left| { - 3{x^2} + 4x + 4} \right|\) tại 4 điểm phân biệt. A. \(0 < m < \dfrac{2}{9}\) B. \(0 < m < \dfrac{{16}}{9}\) C. \(0 < m < \dfrac{{16}}{3}\) D. \(0 < m < 5\) Câu 24. Cho tam giác ABC có G là trọng tâm, I là trung điểm của cạnh AB, M thuộc cạnh AB sao cho\(\overrightarrow {MA} + 3\overrightarrow {MB} = \overrightarrow 0 \). Giả sử điểm N thỏa mãn \(\overrightarrow {AN} = x\overrightarrow {AC} \). Tìm x để ba điểm M, N, G thẳng hàng. A. \(x = \dfrac{3}{5}\) B. \(x = - \dfrac{3}{5}\) C. \(x = \dfrac{4}{5}\) D. \(x = - \dfrac{4}{5}\) Câu 25. Tìm hai điểm phân biệt đối xứng với nhau qua Oy và cùng thuộc đồ thị hàm số \(y = {x^4} - {x^3} - 2{x^2} + 4x - 8\). A. \(M\left( {3;1} \right);M\left( { - 3;1} \right)\) B. \(M\left( {2;1} \right);M\left( { - 2;1} \right)\) C. \(M\left( {3;0} \right);M\left( { - 3;0} \right)\) D. \(M\left( {2;0} \right);M'\left( { - 2;0} \right)\) Lời giải chi tiết
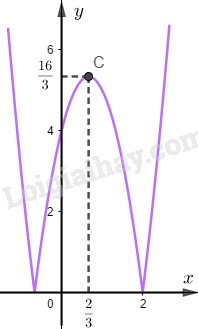
Câu 1. Ta có \(\overrightarrow b - \overrightarrow a = \left( {1 - 3;0 - \left( { - 1} \right)} \right) = \left( { - 2;1} \right)\) Câu 4. ĐKXĐ: \(\left\{ \begin{array}{l}{x^2} - 3 \ne 0\\x + 4 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 4\\x \ne \pm \sqrt 3 \end{array} \right.\) Câu 5. Các phần tử có trong \(B\) mà không có trong \(A\) là: 1 và 3 nên \(B\backslash A = \left\{ {1;3} \right\}\). Các phần tử chung của A và B là: 2;4\( \to A \cap B = \left\{ {2;4} \right\}\) Các phần tử có trong A hoặc trong B là: 0;1;2;3;4;5;6.\( \to A \cup B = \left\{ {0;1;2;3;4;5;6} \right\}\) Các phần tử có trong A mà không có trong B là: 0;5;6 \( \to A\backslash B = \left\{ {0;5;6} \right\}\) Câu 6. Từ đồ thị ta thấy hàm số đi lên trên khoảng \(\left( {1;2} \right)\) mà \(\left( {1;\dfrac{3}{2}} \right) \subset \left( {1;2} \right)\). Nên hàm số đồng biến trên \(\left( {1;\dfrac{3}{2}} \right)\). Câu 8. Hàm số \(y = \sqrt {x + 1} + \sqrt {1 - x} \) có tập xác định \(D = \left[ { - 1;1} \right]\) và \(f\left( x \right) = f\left( { - x} \right)\forall x \in D\). Hàm số \(y = {x^2} + 1\) xác định trên \(\mathbb{R}\) và \(f\left( x \right) = f\left( { - x} \right)\forall x \in \mathbb{R}\). Hàm số \(y = {x^3} - x\) là các hàm lẻ. Hàm số \(y = - 2x + 1\) không chẵn không lẻ. Câu 9. Vì \(x \in \mathbb{Z}\) nên \(A = \left\{ {x \in \mathbb{Z}\left| { - 1 \le x \le 1} \right.} \right\}\). Số phần tử của A là 3. Nên số tập con của A là \({2^3} = 8\) Câu 10. \(A'\left( { - x; - y} \right)\) đối xứng \(A\left( {x;y} \right)\) qua gốc tọa độ. Câu 11. \( - {x^4} + 2{x^2} + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} = - 1\\{x^2} = 3\end{array} \right.\) \( \Leftrightarrow {x^2} = 3 \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 3 \\x = - \sqrt 3 \end{array} \right.\) Câu 12. Hoành độ giao điểm của đường thẳng \(y = - x + 1\) và (P) là nghiệm của phương trình \(4{x^2} - 5x + 2 = - x + 1 \Leftrightarrow 4{x^2} - 4x + 1 = 0\)\( \Leftrightarrow x = \dfrac{1}{2}\) Giao điểm cần tìm là \(M\left( {\dfrac{1}{2};\dfrac{1}{2}} \right)\). Câu 13. Điểm \(I\left( {1;0} \right)\) và \(A\left( { - 1; - 2} \right)\) thuộc đồ thị hàm số \(y = 2a{x^2} - bx + 3\) nên: \(\left\{ \begin{array}{l}2a - b + 3 = 0\\2a + b + 3 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = - 1\end{array} \right.\)\( \Rightarrow S = 5\) Câu 14. Các phương trình hệ quả của phương trình \(\sqrt {2x + 1} = x - 2\) là: (2),(3),(4). Câu 15. Tịnh tiến đồ thị lên trên 2 đơn vị ta được đồ thị hàm số \(y = \left| {2x + 3} \right| - x + 3\) Tịnh tiến đồ thị sang trái 3 đơn vị ta được đồ thị của hàm số \(y = \left| {2\left( {x + 3} \right) + 3} \right| - \left( {x + 3} \right) + 3 = \left| {2x + 9} \right| - x\). Câu 16. \(\overrightarrow {AB} = 4\overrightarrow {MA} \Rightarrow \overrightarrow {MB} = \overrightarrow {MA} + \overrightarrow {AB} = 5\overrightarrow {MA} \) \(\begin{array}{l}\overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {BC} = \overrightarrow {MB} + \overrightarrow {AD} \\ = \overrightarrow {MB} + \overrightarrow {MD} - \overrightarrow {MA} = \overrightarrow {MB} + \overrightarrow {MD} - \dfrac{1}{5}\overrightarrow {MB} \\ = \dfrac{4}{5}\overrightarrow {MB} + \overrightarrow {MD} \end{array}\) Câu 17. Hoành độ giao điểm của đồ thị hai hàm số \(\left( P \right):y = 2{x^2} + 5x - 2\) và \(\left( {P'} \right):y = {x^2} + 4\) là nghiệm của phương trình \(2{x^2} + 5x - 2 = {x^2} + 4\) \(\begin{array}{l} \Leftrightarrow {x^2} + 5x - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = 5\\x = - 6 \Rightarrow y = 40\end{array} \right.\end{array}\) Vậy giao điểm của hai đồ thị là \(\left( {1;5} \right);\left( { - 6;40} \right)\) Câu 18. Ta có \(\Delta = {m^2} + 4\left( {3 - m} \right)\) Hàm số có giá trị lớn nhất bằng \( - \dfrac{\Delta }{{4a}}\) nên \( - \dfrac{{{m^2} - 4m + 12}}{{ - 4}} = 3\) \( \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 4\end{array} \right.\) Câu 19. Bề lõm hướng lên trên nên \(a > 0\). Giao của đồ thị với Oy ở dưới trục hoành nên \(c < 0\). Hoành độ đỉnh dương nên \(b < 0\) Câu 20. Đồ thị của hàm số \(y = - {x^2} + 2x + 2\) có đỉnh \(A\left( {1;3} \right)\) bề lõm hướng xuống dưới, đồng biến trên \(\left( { - \infty ;1} \right)\) và nghịch biến trên \(\left( {1; + \infty } \right)\). Câu 21. \(2mx + 3 = 3{m^2} - 2x \Leftrightarrow \left( {2m + 2} \right)x = 3{m^2} - 3\) Phương trình nghiệm đúng \(\forall x \in \mathbb{R}\) khi \(\left\{ \begin{array}{l}2m + 2 = 0\\3{m^2} - 3 = 0\end{array} \right. \Leftrightarrow m = - 1\) Câu 22. Sau 1 năm người này nợ thêm 50 000 000.4,8%=2 400 000 (VNĐ) Sau n năm người này nợ thêm 2 400 000 .n (VNĐ) Sau 5 năm người này nợ 2 400 000.5+50 000 000=62 000 000 (VNĐ) Câu 23. Vẽ đồ thị hàm số \(\left( P \right):y = \left| { - 3{x^2} + 4x + 4} \right|\):
Đồ thị \(\left( P \right):y = \left| { - 3{x^2} + 4x + 4} \right|\) như hình dưới: Từ đồ thị ta thấy đường thẳng \(y = 3m\) cắt (P) tại 4 điểm phân biệt \( \Leftrightarrow 0 < 3m < \dfrac{{16}}{3} \Leftrightarrow 0 < m < \dfrac{{16}}{9}\) Câu 24. \(\overrightarrow {MA} + 3\overrightarrow {MB} = \overrightarrow 0 \)(1) Ta có \((1) \Leftrightarrow \) \(\overrightarrow {GM} = \dfrac{1}{4}\overrightarrow {GA} + \dfrac{3}{4}\overrightarrow {GB} \) Ta có \(\overrightarrow {AN} = x\overrightarrow {AC} \Leftrightarrow \overrightarrow {GN} = (1 - 2x)\overrightarrow {GA} - x\overrightarrow {GB} \) Ba điểm M, N, G thẳng hàng \( \Leftrightarrow \overrightarrow {GM} ,\overrightarrow {GN} \) cùng phương \( \Leftrightarrow \dfrac{{1 - 2x}}{{\dfrac{1}{4}}} = \dfrac{{ - x}}{{\dfrac{3}{4}}} \Leftrightarrow x = \dfrac{3}{5}\) Câu 25. Gọi M(x;y) và M’(x;-y) là hai điểm phân biệt đối xứng nhau qua Oy (\(x \ne 0\)) M và M’ thuộc đồ thị hàm số nên \(\left\{ \begin{array}{l}y = {x^4} - {x^3} - 2{x^2} + 4x - 8\\y = {x^4} + {x^3} - 2{x^2} - 4x - 8\end{array} \right.\) \( \Rightarrow 2\left( { - {x^3} + 4x} \right) = 0\) \( \Rightarrow \left[ \begin{array}{l}x = 2 \Rightarrow y = 0\\x = - 2 \Rightarrow y = 0\\x = 0\left( L \right)\end{array} \right.\) Vậy M(2;0) và M’(-2;0). HocTot.XYZ
|