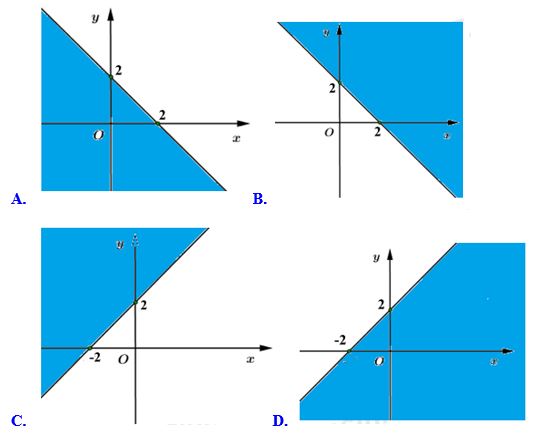
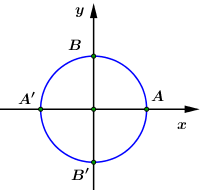
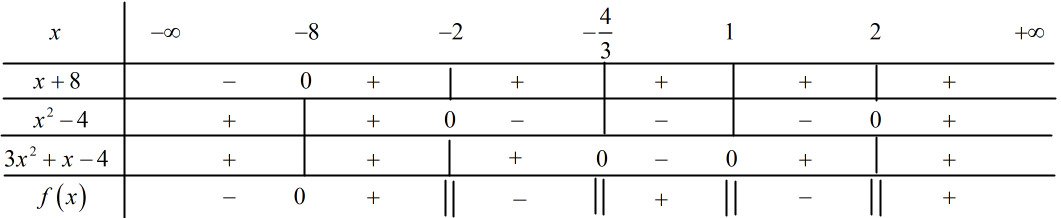Đề số 10 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10Đáp án và lời giải chi tiết Đề số 10 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 10 Đề bài I. Phần tự luận (5 điểm) Câu 1 (2 điểm): Giải các bất phương trình sau: a) \(\frac{1}{{{x^2} - 4}} \le \frac{3}{{3{x^2} + x - 4}}\) b) \(\sqrt {x + 1} - \sqrt {x - 7} \ge 2\) Câu 2 (1 điểm): Rút gọn biểu thức: \(E = \sin 6x - 2\sin x\left( {\cos 3x + \cos 5x} \right).\) Câu 3 (2 điểm): Cho đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 2x + 4y - 4 = 0\) và đường thẳng \(d:\,\,\,3x - 4y + 4 = 0.\) a) Xác định tâm và bán kính đường tròn \(\left( C \right).\) Viết phương trình đường thẳng \(\Delta \) song song với đường thẳng \(d\) và tiếp xúc với \(\left( C \right).\) b) Viết phương trình đường thẳng đi qua điểm \(A\left( {0; - 1} \right)\) cắt \(\left( C \right)\) tại hai điểm \(M,\,\,N\) sao cho độ dài dây cung \(MN\) là ngắn nhất. II. Phần trắc nghiệm (5 điểm) Câu 1: Cho \(\sin \alpha = \frac{4}{5},\,\,\,\left( {{{90}^0} < \alpha < {{180}^0}} \right).\) Tính \(\cos \alpha .\) A. \(\cos \alpha = - \frac{3}{5}\) B. \(\cos \alpha = - \frac{4}{5}\) C. \(\cos \alpha = \frac{3}{5}\) D. \(\cos \alpha = \frac{5}{3}\) Câu 2: Miền nghiệm của bất phương trình \(x + y > 2\) là phần không tô đậm trong hình vẽ nào? Câu 3: Cho \(A,\,\,B,\,\,C\) là ba góc của một tam giác. Hãy chọn hệ thức đúng trong các hệ thức sau. A. \(\sin 2A + \sin 2B + \sin 2C\) \( = 4\cos A\cos B\cos C\) B. \(\sin 2A + \sin 2B + \sin 2C\)\( = 4\sin A\sin B\sin C\) C. \(\sin 2A + \sin 2B + \sin 2C\) \( = - 4\sin A\sin B\sin C\) D. \(\sin 2A + \sin 2B + \sin 2C\)\( = 1 - 4\sin A\sin B\sin C\) Câu 4: Cho elip có phương trình:\(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1.\) Khi đó tọa độ tiêu điểm của elip là: A. \({F_1}\left( { - 4;\,\,0} \right),\,\,{F_2}\left( {4;\,\,0} \right)\) B. \({F_1}\left( { - 3;\,\,0} \right),\,\,{F_2}\left( {3;\,\,0} \right)\) C. \({F_1}\left( { - 16;\,\,0} \right),\,\,{F_2}\left( {16;\,\,0} \right)\) D. \({F_1}\left( { - 5;\,\,0} \right),\,\,{F_2}\left( {5;\,\,0} \right)\) Câu 5: Người ta dùng 100m rào để rào một mảnh vườn hình chữ nhật để thả gia súc. Diện tích lớn nhất của mảnh vườn có thể rào được là: A. \(10\,000{m^2}\) B. \(600\,{m^2}\) C. \(625\,{m^2}\) D. \(500\,{m^2}\) Câu 6: Khoảng cách từ điểm \(M\left( {0;\,\,1} \right)\) đến đường thẳng \(d:\,\,5x - 12y - 1 = 0\) là: A. \(\frac{{11}}{{13}}\) B. \(\frac{{13}}{{17}}\) C. \( - 1\) D. \(1\) Câu 7: Tập nghiệm của bất phương trình \(\frac{{x + 1}}{{3 - 2x}} \le 0\) là: A. \(\left[ { - 1;\,\,\frac{3}{2}} \right]\) B. \(\left( { - \infty ; - 1} \right] \cup \left[ {\frac{3}{2}; + \infty } \right)\) C. \(\left( { - \infty ; - 1} \right] \cup \left( {\frac{3}{2}; + \infty } \right)\) D. \(\left[ { - 1;\,\,\frac{3}{2}} \right)\) Câu 8: Cho bất phương trình: \(\frac{8}{{2 - x}} > 1\,\,\,\left( 1 \right).\) Một học sinh giải như sau: \(\left( 1 \right)\mathop \Leftrightarrow \limits^{\left( I \right)} \frac{1}{{2 - x}} > \frac{1}{8}\mathop \Leftrightarrow \limits^{\left( {II} \right)} \left\{ \begin{array}{l}x \ne 2\\2 - x < 8\end{array} \right.\\\mathop \Leftrightarrow \limits^{\left( {III} \right)} \left\{ \begin{array}{l}x \ne 2\\x > 6\end{array} \right..\) Hỏi học sinh này giải sai từ bước nào? A. \(\left( {II} \right)\) B. \(\left( {III} \right)\) C. \(\left( I \right)\) D. Không sai Câu 9: Rút gọn biểu thức \(P\) (với điều kiện của \(x\) để \(P\) có nghĩa) \(P = \frac{{\sin 2x\cos x}}{{\left( {1 + \cos 2x} \right)\left( {1 + \cos x} \right)}}.\) A. \(P = \tan x\) B. \(P = - \tan \frac{x}{2}\) C. \(P = \cot \frac{x}{2}\) D. \(P = \tan \frac{x}{2}\) Câu 10: Phương trình nào sau đây là phương trình đường tròn? A. \({x^2} + 2{y^2} - 4x + 6y - 1 = 0\) B. \({x^2} + {y^2} - 4x - 8y + 1 = 0\) C. \({x^2} + {y^2} - 2x - 8y + 20 = 0\) D. \({x^2} + {y^2} - 10xy + 4y - 2 = 0\) Câu 11: Cho đường thẳng \({d_1}:\,\,2x + y + 15 = 0\) và \({d_2}:\,\,x - 2y - 3 = 0.\) Khẳng định nào sau đây đúng? A. \({d_1}\) và \({d_2}\) vuông góc với nhau B. \({d_1}\) và \({d_2}\) cắt nhau và không vuông góc với nhau C. \({d_1}\) và \({d_2}\) trùng nhau D. \({d_1}\) và \({d_2}\) song song với nhau Câu 12: Biểu thức \(\frac{{{{\cos }^3}x\sin x - {{\sin }^3}x\cos x}}{{\sin 4x}}\) không phụ thuộc \(x\) và bằng: A. \(4\) B. \(1\) C. \(\frac{1}{4}\) D. \(\frac{3}{4}\) Câu 13: Tìm tập nghiệm \(S\) của bất phương trình: \( - 2{x^2} - 3x + 2 > 0.\) A. \(S = \left( { - \frac{1}{2};\,\,2} \right)\) B. \(S = \left( { - 2;\,\,\frac{1}{2}} \right)\) C. \(S = \left( { - \infty ; - 2} \right) \cup \left( {\frac{1}{2}; + \infty } \right)\) D. \(S = \left( { - \infty ; - \frac{1}{2}} \right) \cup \left( {2; + \infty } \right)\) Câu 14: Cung nào sau đây có điểm đầu là \(A\) điểm cuối trùng với \(B\) hoặc \(B'?\)
A. \(\alpha = - {90^0} + k{180^0}\,\,\,\left( {k \in \mathbb{Z}} \right)\) B. \(\alpha = {90^0} + k{360^0}\,\,\,\left( {k \in \mathbb{Z}} \right)\) C. \(\alpha = - {90^0} + k{\pi ^0}\,\,\,\left( {k \in \mathbb{Z}} \right)\) D. \(\alpha = - \frac{\pi }{2} + k2\pi \,\,\,\,\left( {k \in \mathbb{Z}} \right)\) Câu 15: Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \sqrt {{x^2} - 2mx - 2m + 3} \) có tập xác định là \(\mathbb{R}?\) A. 6 B. 3 C. 5 D. 4 Câu 16: Cho \(\Delta ABC.\) Khẳng định nào sau đây là sai? A. \(\sin \frac{{A + C}}{2} = \cos \frac{B}{2}\) B. \(\cos \left( {A + B} \right) = \cos C\) C. \(\sin \frac{{A + B + 3C}}{2} = \cos C\) D. \(\sin \left( {A + B} \right) = \sin C\) Câu 17: Giá trị biểu thức \(\frac{{\sin \frac{\pi }{{15}}\cos \frac{\pi }{{10}} + \sin \frac{\pi }{{10}}\cos \frac{\pi }{{15}}}}{{\cos \frac{{2\pi }}{{15}}\cos \frac{\pi }{5} - \sin \frac{{2\pi }}{{15}}\sin \frac{\pi }{5}}}\) là: A. \( - \frac{3}{2}\) B. \( - 1\) C. \(1\) D. \(\frac{{\sqrt 3 }}{2}\) Câu 18: Cho hai điểm \(A\left( { - 2;\,0} \right)\) và \(B\left( {4;\,\,0} \right).\) Tìm tọa độ điểm \(M\) thuộc trục \(Oy\) sao cho \(\Delta MAB\) có diện tích bằng \(3.\) A. \(M\left( {0; - 2} \right),\,\,M\left( {0;\,\,2} \right)\) B. \(M\left( {0; - 1} \right),\,\,M\left( {0;\,\,1} \right)\) C. \(M\left( {0; - 3} \right),\,\,M\left( {0;\,\,3} \right)\) D. \(M\left( { - 1;\,\,0} \right),\,\,M\left( {1;\,\,0} \right)\) Câu 19: Cho \(\frac{\pi }{4} < \frac{a}{2} < \frac{\pi }{2}.\) Khẳng định đúng là: A. \(\sin a > 0,\,\,\,\cos a > 0\) B. \(\sin a > 0,\,\,\,\cos a < 0\) C. \(\sin a < 0,\,\,\,\cos a > 0\) D. \(\sin a < 0,\,\,\,\cos a < 0\) Câu 20: Số nghiệm nguyên của bất phương trình: \(\left| {2x - 3} \right| \le 5\) là: A. 7 B. 4 C. 6 D. 5 Lời giải chi tiết I. Phần tự luận (5 điểm) Câu 1 (VD) Phương pháp: a) Đặt điều kiện để bất phương trình có nghĩa. Biến đổi bất phương trình. Lập bảng xét dấu để giải bất phương trình. b) Đặt điều kiện, biến đổi, giải bất phương trình chứa căn thức bậc hai. \(\sqrt {f\left( x \right)} \ge \sqrt {g\left( x \right)} + a\,\,\,\,\left( {a > 0} \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) \ge 0\\f\left( x \right) \ge {\left( {g\left( x \right) + a} \right)^2}\end{array} \right..\) Cách giải: a) \(\frac{1}{{{x^2} - 4}} \le \frac{3}{{3{x^2} + x - 4}}\,\,\,\,\left( * \right)\) Điều kiện:\(\left\{ \begin{array}{l}{x^2} - 4 \ne 0\\3{x^2} + x - 4 \ne 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ne \pm 2\\x \ne 1\\x \ne - \frac{4}{3}\end{array} \right..\) \(\begin{array}{l}\left( * \right) \Leftrightarrow \frac{1}{{{x^2} - 4}} - \frac{3}{{3{x^2} + x - 4}} \le 0\\ \Leftrightarrow \frac{{3{x^2} + x - 4 - 3\left( {{x^2} - 4} \right)}}{{\left( {{x^2} - 4} \right)\left( {3{x^2} + x - 4} \right)}} \le 0\\ \Leftrightarrow \frac{{x + 8}}{{\left( {{x^2} - 4} \right)\left( {3{x^2} + x - 4} \right)}} \le 0\end{array}\) Đặt \(f\left( x \right) = \frac{{x + 8}}{{\left( {{x^2} - 4} \right)\left( {3{x^2} + x - 4} \right)}}\) Ta có bảng xét dấu:
\( \Rightarrow f\left( x \right) \le 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 8\\ - 2 < x < - \frac{4}{3}\\1 < x < x\end{array} \right..\) Vậy tập nghiệm của bất phương trình đã cho là: \(S = \left( { - \infty ; - 8} \right] \cup \left( { - 2; - \frac{4}{3}} \right) \cup \left( {1;\,\,2} \right).\) b) \(\sqrt {x + 1} - \sqrt {x - 7} \ge 2\) \(\begin{array}{l} \Leftrightarrow \sqrt {x + 1} \ge 2 + \sqrt {x - 7} \\ \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\x - 7 \ge 0\\x + 1 \ge {\left( {2 + \sqrt {x - 7} } \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\x \ge 7\\x + 1 \ge 4 + 4\sqrt {x - 7} + x - 7\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 7\\4\sqrt {x - 7} \le 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 7\\\sqrt {x - 7} \le 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 7\\x - 7 \le 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 7\\x \le 8\end{array} \right.\\ \Leftrightarrow 7 \le x \le 8.\end{array}\) Vậy tập nghiệm của bất phương trình đã cho là: \(S = \left[ {7;\,\,8} \right].\) Câu 2 (VD) Phương pháp: Sử dụng các công thức: \(\left\{ \begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\\\sin a.\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\\\sin 2a = 2\sin a\cos a\end{array} \right..\) Cách giải: \(\begin{array}{l}E = \sin 6x - 2\sin x\left( {\cos 3x + \cos 5x} \right)\\\,\,\,\,\, = \sin 6x - 2\sin x.2.\cos 4x.\cos \left( { - x} \right)\\\,\,\,\,\, = \sin 6x - 4\sin x.\cos 4x.\cos x\\\,\,\,\,\, = \sin 6x - 2\sin 2x.\cos 4x\\\,\,\,\,\, = \sin 6x - \left( {\sin 6x + \sin \left( { - 2x} \right)} \right)\\\,\,\,\,\, = \sin 6x - \sin 6x + \sin 2x\\\,\,\,\,\, = \sin 2x.\end{array}\) Vậy \(E = \sin 2x.\) Câu 3 (VD) Phương pháp: a) Đường tròn \(\left( C \right):\,\,\,{x^2} + {y^2} - 2ax - 2by + c = 0\) có tâm \(I\left( {a;\,\,b} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} .\) Đường thẳng \(\Delta //d \Rightarrow \overrightarrow {{n_d}} \) chính là VTPT của \(\Delta .\) Phương trình đường thẳng \(d\) đi qua \(M\left( {{x_0};\,\,{y_0}} \right)\) và có VTPT \(\overrightarrow n = \left( {A;\,\,B} \right)\) có dạng: \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) = 0.\) b) Giả sử đường thẳng \(d\) cắt đường tròn \(\left( C \right)\) có tâm \(I\) và bán kính \(R\) theo dây cung \(AB.\) Khi đó áp dụng định lý Pitago ta có: \({R^2} = {d^2}\left( {I;\,\,d} \right) + {\left( {\frac{{AB}}{2}} \right)^2}.\) Cách giải: Cho đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 2x + 4y - 4 = 0\) và đường thẳng \(d:\,\,\,3x - 4y + 4 = 0.\) a) Xác định tâm và bán kính đường tròn \(\left( C \right).\) Viết phương trình đường thẳng \(\Delta \) song song với đường thẳng \(d\) và tiếp xúc với \(\left( C \right).\) Xét phương trình đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 2x + 4y - 4 = 0\) ta có: \(a = 1,\,\,b = - 2,\,\,x = - 4\) \( \Rightarrow \left( C \right)\) có tâm \(I\left( {1; - 2} \right)\) và bán kính \(R = \sqrt {{1^2} + {{\left( { - 2} \right)}^2} + 4} = 3.\) Ta có:\(d:\,\,\,3x - 4y + 4 = 0\) có VTPT \(\overrightarrow {{n_d}} = \left( {3;\,\, - 4} \right).\) \( \Rightarrow \) Đường thẳng \(\Delta //d\) có phương trình : \(3x - 4y + c = 0\,\,\,\,\left( {c \ne 4} \right).\) \(\Delta \) tiếp xúc với \(\left( C \right) \Rightarrow d\left( {I;\,\,\Delta } \right) = R = 3\) \(\begin{array}{l} \Leftrightarrow \frac{{\left| {3.1 - 4.\left( { - 2} \right) + c} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 3\\ \Leftrightarrow \left| {11 + c} \right| = 15\\ \Leftrightarrow \left[ \begin{array}{l}11 + c = 15\\11 + c = - 15\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}c = 4\,\,\,\,\left( {ktm} \right)\\c = - 26\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy \(\Delta :\,\,\,3x - 4y - 26 = 0.\) b) Viết phương trình đường thẳng đi qua điểm \(A\left( {0; - 1} \right)\) cắt \(\left( C \right)\) tại hai điểm \(M,\,\,N\) sao cho độ dài dây cung \(MN\) là ngắn nhất. Ta có: \(\overrightarrow {AI} = \left( {1; - 1} \right) \Rightarrow AI = \sqrt 2 < R\) \( \Rightarrow A\) nằm trong đường tròn \(\left( C \right).\) Gọi \(H\) là trung điểm của \(MN \Rightarrow IH \bot MN\) hay \(d\left( {I;\,\,MN} \right) = IH\) và \(MN = 2MH.\) \( \Rightarrow MN\) ngắn nhất \( \Leftrightarrow MH\) ngắn nhất. Lại có: \(MH = \sqrt {{R^2} - I{H^2}} \) \( \Rightarrow MH\) ngắn nhất \( \Leftrightarrow IH\) lớn nhất \( \Leftrightarrow d\left( {I;\,\,MN} \right) = IA.\) \( \Rightarrow d'\) đi qua điểm \(A\left( {0; - 1} \right)\) và có VTPT là: \(\overrightarrow {AI} = \left( {1; - 1} \right)\) \( \Rightarrow d':\,\,\,x - y + 1 = 0.\) II. Phần trắc nghiệm (5 điểm)
Câu 1 (TH) Phương pháp: Với \({90^0} < \alpha < {180^0}\) thì \(\sin \alpha > 0,\,\,\,\cos \alpha < 0.\) Sử dụng công thức: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1.\) Cách giải: Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) \( \Leftrightarrow {\cos ^2}\alpha = 1 - {\left( {\frac{4}{5}} \right)^2} = \frac{9}{{25}}.\) Lại có: \({90^0} < \alpha < {180^0}\) thì \(\sin \alpha > 0,\,\,\,\cos \alpha < 0.\) \( \Rightarrow \cos \alpha = - \sqrt {\frac{9}{{25}}} = - \frac{3}{5}.\) Chọn A. Câu 2 (TH) Phương pháp: Sử dụng quy tắc thực hành biểu diễn hình học tâp nghiệm (hay biểu diễn miền nghiệm) của bất phương trình \(x + y \ge 2\) trên mặt phẳng tọa độ. Cách giải: Trên mặt phẳng \(Oxy,\) vẽ đồ thị hàm số \(d:\,\,\,x + y = 2 \Rightarrow \)loại đáp án C, D. Ta thấy điểm \(O\left( {0;\,\,0} \right)\) không thuộc đường thẳng \(d:\,\,\,x + y = 2.\) Khi đó ta có:\(0 + 0 = 0 < 2 \Rightarrow O\left( {0;\,\,0} \right)\) không thuộc miền nghiệm của bất phương trình \(x + y \ge 2.\) Chọn A. Câu 3 (TH) Phương pháp: Ta có: \(A,\,\,B,\,\,C\) là ba góc của một tam giác \( \Rightarrow A + B + C = {180^0}.\) Sử dụng công thức: \(\left\{ \begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos \left( {{{180}^0} - x} \right) = - \cos x\\\cos \left( {{{90}^0} - x} \right) = \sin x\end{array} \right..\) Cách giải: Ta có: \(\sin 2A + \sin 2B + \sin 2C\) \(\begin{array}{l} = \sin 2A + 2\sin \frac{{2B + 2C}}{2}\cos \frac{{2B - 2C}}{2}\\ = 2\sin A\cos A + 2\sin \left( {B + C} \right)\cos \left( {B - C} \right)\\ = 2\sin A\cos A + 2\sin \left( {{{180}^0} - A} \right)\cos \left( {B - C} \right)\\ = 2\sin A\cos A + 2\sin A\cos \left( {B - C} \right)\\ = 2\sin A\left[ {\cos A + \cos \left( {B - C} \right)} \right]\\ = 2\sin A.2\cos \frac{{A + B - C}}{2}.\cos \frac{{A - B + C}}{2}\\ = 4\sin A.\cos \frac{{{{180}^0} - 2C}}{2}.\cos \frac{{{{180}^0} - 2B}}{2}\\ = 4\sin A.\cos \left( {{{90}^0} - C} \right).\cos \left( {{{90}^0} - B} \right)\\ = 4\sin A\sin B\sin C.\end{array}\) Chọn B. Câu 4 (TH) Phương pháp: Cho elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) thì tọa độ tiêu điểm là: \({F_1}\left( { - c;\,\,0} \right)\) và \({F_2}\left( {c;\,\,0} \right)\) với \({c^2} = {a^2} - {b^2}.\) Cách giải: Ta có: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1 \Rightarrow \left\{ \begin{array}{l}{a^2} = 25\\{b^2} = 9\end{array} \right.\) \( \Rightarrow {c^2} = 25 - 9 = 16 \Rightarrow c = 4\) \( \Rightarrow \) Tọa độ các tiêu điểm của elip là: \({F_1}\left( { - 4;\,\,0} \right)\) và \({F_2}\left( {4;\,\,0} \right).\) Chọn A. Câu 5 (VD) Phương pháp: Gọi chiều dài của mảnh vườn là \(x\,\,\left( m \right)\,\,\,\left( {0 < x < 50} \right).\) Dựa vào công thức tính diện tích của hình chữ nhật để lập biểu thức của \(x\) rồi tìm giá trị lớn nhất theo \(x.\) Cách giải: Nửa chu vi của mảnh vườn là: \(100:2 = 50\,\,m.\) Gọi chiều dài của mảnh vườn là \(x\,\,\left( m \right)\,\,\,\left( {0 < x < 50} \right).\) Khi đó chiều rộng của mảnh vườn là: \(50 - x\,\,\left( m \right).\) Khi đó diện tích của mảnh vườn là: \(S = x\left( {50 - x} \right) = - {x^2} + 50x\) \( = - {\left( {x - 25} \right)^2} + 625 \le 625\) Vậy diện tích lớn nhất của mảnh vườn là \(625\,{m^2}.\) Chọn C. Câu 6 (TH) Phương pháp: Cho điểm \(M\left( {{x_0};\,\,{y_0}} \right)\) và đường thẳng \(d:\,\,\,ax + by + c = 0\) ta có: \(d\left( {M;\,\,d} \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\) Cách giải: Ta có: \(d\left( {M;\,\,d} \right) = \frac{{\left| {5.0 - 12.1 - 1} \right|}}{{\sqrt {{5^2} + {{12}^2}} }}\) \( = \frac{{13}}{{13}} = 1.\) Chọn D. Câu 7 (TH) Phương pháp: Giải bất phương trình bậc nhất 1 ẩn: \(\frac{A}{B} \le 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}A \le 0\\B > 0\end{array} \right.\\\left\{ \begin{array}{l}A \ge 0\\B < 0\end{array} \right.\end{array} \right..\) Cách giải: \(\begin{array}{l}\frac{{x + 1}}{{3 - 2x}} \le 0\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x + 1 \ge 0\\3 - 2x < 0\end{array} \right.\\\left\{ \begin{array}{l}x + 1 \le 0\\3 - 2x > 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge - 1\\x > \frac{3}{2}\end{array} \right.\\\left\{ \begin{array}{l}x \le - 1\\x < \frac{3}{2}\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x > \frac{3}{2}\\x \le - 1\end{array} \right..\end{array}\) Vậy tập nghiệm của bất phương trình là: \(S = \left( { - \infty ; - 1} \right] \cup \left( {\frac{3}{2}; + \infty } \right).\) Chọn C. Câu 8 (TH) Phương pháp: Chuyển vế, đổi dấu và giải bất phương trình bậc nhất một ẩn. Cách giải: \(\begin{array}{l}\frac{8}{{2 - x}} > 1\,\, \Leftrightarrow \frac{1}{{2 - x}} > \frac{1}{8}\\ \Leftrightarrow \frac{1}{{2 - x}} - \frac{1}{8} > 0\\ \Leftrightarrow \left\{ \begin{array}{l}2 - x \ne 0\\\frac{{8 - 2 + x}}{{8\left( {2 - x} \right)}} > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\\frac{{x - 6}}{{2 - x}} > 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 6 > 0\\2 - x > 0\end{array} \right.\\\left\{ \begin{array}{l}x - 6 < 0\\2 - x < 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 6\\x < 2\end{array} \right.\\\left\{ \begin{array}{l}x < 6\\x > 2\end{array} \right.\end{array} \right.\\ \Leftrightarrow 2 < x < 6.\end{array}\) Như vậy bạn học sinh đã sai từ bước II. Chọn A. Câu 9 (TH) Phương pháp: Sử dụng các công thức: \(\left\{ \begin{array}{l}\sin 2x = 2\sin x\cos x\\\tan x = \frac{{\sin x}}{{\cos x}}\\1 + \cos 2x = 2{\cos ^2}x\end{array} \right..\) Cách giải: \(\begin{array}{l}P = \frac{{\sin 2x\cos x}}{{\left( {1 + \cos 2x} \right)\left( {1 + \cos x} \right)}}\\ = \frac{{2\sin x{{\cos }^2}x}}{{2{{\cos }^2}x\left( {1 + \cos x} \right)}}\\ = \frac{{\sin x}}{{2{{\cos }^2}\frac{x}{2}}} = \frac{{2\sin \frac{x}{2}\cos \frac{x}{2}}}{{2{{\cos }^2}\frac{x}{2}}}\\ = \frac{{\sin \frac{x}{2}}}{{\cos \frac{x}{2}}} = \tan \frac{x}{2}.\end{array}\) Chọn D. Câu 10 (TH) Phương pháp: Phương trình \({x^2} + 2{y^2} - 2ax - 2by + c = 0\) là phương trình đường tròn \( \Leftrightarrow {a^2} + {b^2} - c > 0.\) Phương trình đường tròn có hệ số của \({x^2}\) và \({y^2}\) bằng nhau và \({a^2} + {b^2} - c > 0.\) Cách giải: +) Xét đáp án A: \({x^2} + 2{y^2} - 4x + 6y - 1 = 0\) không là phương trình đường tròn vì hệ số của \({x^2}\) và \({y^2}\) khác nhau. +) Xét đáp án B: \({x^2} + {y^2} - 4x - 8y + 1 = 0\) có \(a = 2,\,\,b = 4,\,\,c = 1\) \( \Rightarrow {a^2} + {b^2} - c\) \( = {2^2} + {4^2} - 1 = 19 > 0\) \( \Rightarrow \) đây là phương trình đường tròn. Chọn B. Câu 11 (NB) Phương pháp: Xét hai đường thẳng: \({d_1}:\,\,\,ax + by + c = 0\) và \({d_2}:\,\,a'x + b'y + c' = 0\) ta có: +) \({d_1} \bot {d_2} \Leftrightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0.\) +) \({d_1}//{d_2} \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {{n_1}} = k\overrightarrow {{n_2}} \\c \ne c'\end{array} \right.\) \( \Leftrightarrow \frac{a}{{a'}} = \frac{b}{{b'}} \ne \frac{c}{{c'}}.\) +) \({d_1}\) cắt \({d_2} \Leftrightarrow \overrightarrow {{n_1}} \) không cùng phương với \(\overrightarrow {{n_2}} \Leftrightarrow \frac{a}{{a'}} \ne \frac{b}{{b'}}.\) +) \({d_1}\) trùng với \({d_2} \Leftrightarrow \frac{a}{{a'}} = \frac{b}{{b'}} = \frac{c}{{c'}}.\) Cách giải: Xét hai đường thẳng \({d_1}:\,\,2x + y + 15 = 0\) và \({d_2}:\,\,x - 2y - 3 = 0\) ta có: \(\overrightarrow {{n_1}} = \left( {2;\,\,1} \right),\,\,\,\overrightarrow {{n_2}} = \left( {1; - 2} \right)\) \(\begin{array}{l} \Rightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 2.1 + 1.\left( { - 2} \right) = 0\\ \Rightarrow {d_1} \bot {d_2}.\end{array}\) Chọn A. Câu 12 (TH) Phương pháp: Sử dụng các công thức: \(\left\{ \begin{array}{l}\sin 2x = 2\sin x\cos x\\{\cos ^2}x - {\sin ^2}x = \cos 2x\end{array} \right..\) Cách giải: \(\begin{array}{l}\frac{{{{\cos }^3}x\sin x - {{\sin }^3}x\cos x}}{{\sin 4x}}\\ = \frac{{\sin x\cos x\left( {{{\cos }^2}x - {{\sin }^2}x} \right)}}{{2\sin 2x\cos 2x}}\\ = \frac{{\frac{1}{2}\sin 2x.\cos 2x}}{{2\sin 2x\cos 2x}} = \frac{1}{4}\end{array}\) \( \Rightarrow \frac{{{{\cos }^3}x\sin x - {{\sin }^3}x\cos x}}{{\sin 4x}}\) là biểu thức không phụ thuộc vào \(x.\) Chọn C. Câu 13 (TH) Phương pháp: Giải bất phương trình bậc hai một ẩn nhờ quy tắc xét dấu của tam thức bậc hai: “Trong khác, ngoài cùng”. Cách giải: Ta có: \( - 2{x^2} - 3x + 2 > 0\) \( \Leftrightarrow 2{x^2} + 3x - 2 < 0\) \(\begin{array}{l} \Leftrightarrow \left( {x + 2} \right)\left( {2x - 1} \right) < 0\\ \Leftrightarrow - 2 < x < \frac{1}{2}.\end{array}\) Chọn B. Câu 14 (VD) Phương pháp: Dựa vào hình vẽ ta có điểm A có cung biểu diễn là: \(\varphi = k2\pi = k{360^0}\,\,\,\left( {k \in \mathbb{Z}} \right).\) Cách giải: Dựa vào hình vẽ ta có điểm B có cung biểu diễn là: \({\varphi _B} = \frac{\pi }{2} + k2\pi \) \( = {90^0} + k{360^0}\,\,\,\left( {k \in \mathbb{Z}} \right).\) Dựa vào hình vẽ ta có điểm B’ có cung biểu diễn là: \({\varphi _{B'}} = - \frac{\pi }{2} + k2\pi \) \( = - {90^0} + k{360^0}\,\,\,\left( {k \in \mathbb{Z}} \right).\) \( \Rightarrow \) Cung biểu diễn điểm B và B’ là: \(\alpha = \frac{\pi }{2} + k\pi \) \( = {90^0} + k{180^0}\,\,\,\left( {k \in \mathbb{Z}} \right).\) Chọn A. Câu 15 (VD) Phương pháp: Hàm số \(y = \sqrt {f\left( x \right)} \) xác định trên \(\mathbb{R}\) \( \Leftrightarrow f\left( x \right) \ge 0\,\,\,\forall x.\) Tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\,\, \ge 0,\) \(\forall x\,\,\,\left( {a > 0} \right)\) \( \Leftrightarrow \Delta \le 0\) Cách giải: Hàm số \(y = \sqrt {{x^2} - 2mx - 2m + 3} \) có tập xác định là \(\mathbb{R}\) \(\begin{array}{l} \Leftrightarrow {x^2} - 2mx - 2m + 3 \ge 0\,\,\,\forall x\\ \Leftrightarrow \Delta ' \le 0\,\,\\ \Leftrightarrow {m^2} + 2m - 3 \le 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 3} \right) \le 0\\ \Leftrightarrow - 3 \le m \le 1.\end{array}\) Lại có: \(m \in \mathbb{Z}\) \( \Rightarrow m \in \left\{ { - 3;\, - 2; - 1;\,\,0;\,\,1} \right\}.\) Vậy có 5 giá trị nguyên của \(m\) thỏa mãn bài toán. Chọn C. Câu 16 (TH) Phương pháp: Ta có: \(A,\,\,B,\,\,C\) là ba góc của một tam giác \( \Rightarrow A + B + C = {180^0}.\) Sử dụng công thức: \(\left\{ \begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos \left( {{{180}^0} - x} \right) = - \cos x\\\cos \left( {{{90}^0} - x} \right) = \sin x\\\sin \left( {{{90}^0} - x} \right) = \cos x\end{array} \right..\) Cách giải: +) Xét đáp án A ta có: \(\sin \frac{{A + C}}{2} = \sin \frac{{{{180}^0} - B}}{2}\)\( = \sin \left( {{{90}^0} - \frac{B}{2}} \right) = \cos \frac{B}{2}\)\( \Rightarrow \) đáp án A đúng. +) Xét đáp án B ta có: \(\cos \left( {A + B} \right) = \cos \left( {{{180}^0} - C} \right)\)\( = - \cos C \ne \cos C\) \( \Rightarrow \) đáp án B sai. Chọn B. Câu 17 (TH) Phương pháp: Sử dụng công thức: \(\left\{ \begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b\\\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b\end{array} \right..\) Cách giải: \(\begin{array}{l}\frac{{\sin \frac{\pi }{{15}}\cos \frac{\pi }{{10}} + \sin \frac{\pi }{{10}}\cos \frac{\pi }{{15}}}}{{\cos \frac{{2\pi }}{{15}}\cos \frac{\pi }{5} - \sin \frac{{2\pi }}{{15}}\sin \frac{\pi }{5}}}\\ = \frac{{\sin \frac{\pi }{{15}}\cos \frac{\pi }{{10}} + \cos \frac{\pi }{{15}}\sin \frac{\pi }{{10}}}}{{\cos \frac{{2\pi }}{{15}}\cos \frac{\pi }{5} - \sin \frac{{2\pi }}{{15}}\sin \frac{\pi }{5}}}\\ = \frac{{\sin \left( {\frac{\pi }{{15}} + \frac{\pi }{{10}}} \right)}}{{\cos \left( {\frac{{2\pi }}{{15}} + \frac{\pi }{5}} \right)}} = \frac{{\sin \frac{\pi }{6}}}{{\cos \frac{\pi }{3}}} = 1.\end{array}\) Chọn C. Câu 18 (VD) Phương pháp: Ta có: \(M\) thuộc trục \(Oy \Rightarrow M\left( {0;\,\,m} \right).\) \({S_{MAB}} = \frac{1}{2}d\left( {M;\,\,AB} \right).AB\) \( \Rightarrow {S_{MAB}} = 3 \Rightarrow m\) Cách giải: Ta có: \(M\) thuộc trục \(Oy \Rightarrow M\left( {0;\,\,m} \right).\) \(A\left( { - 2;\,0} \right)\) và \(B\left( {4;\,\,0} \right)\) \( \Rightarrow AB = \sqrt {{{\left( {4 + 2} \right)}^2}} = 6\) Phương trình đường thẳng \(AB\) đi qua \(A\left( { - 2;\,0} \right)\) và \(B\left( {4;\,\,0} \right)\) là: \(y = 0.\) \(\begin{array}{l} \Rightarrow d\left( {M;\,\,AB} \right) = \frac{{\left| m \right|}}{1} = \left| m \right|.\\ \Rightarrow {S_{MAB}} = \frac{1}{2}d\left( {M;\,\,AB} \right).AB\\ = \frac{1}{2}\left| m \right|.6 = 3\\ \Leftrightarrow \left| m \right| = 1 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 1\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}M\left( {0;\,\,1} \right)\\M\left( {0; - 1} \right)\end{array} \right..\end{array}\) Chọn B. Câu 19 (TH) Phương pháp: Ta có: \(\frac{\pi }{2} < x < \pi \Rightarrow \left\{ \begin{array}{l}\sin x > 0\\\cos x < 0\end{array} \right..\) Cách giải: Ta có: \(\frac{\pi }{4} < \frac{a}{2} < \frac{\pi }{2} \Leftrightarrow \frac{\pi }{2} < a < \pi \) \( \Rightarrow \left\{ \begin{array}{l}\sin a > 0\\\cos a < 0\end{array} \right..\) Chọn B. Câu 20 (VD) Phương pháp: Giải bất phương trình có chứa dấu giá trị tuyệt đối:\(\left| {f\left( x \right)} \right| \le A\,\,\,\left( {A \ge 0} \right)\) \( \Leftrightarrow - A \le f\left( x \right) \le A\) Cách giải: \(\left| {2x - 3} \right| \le 5\)\( \Leftrightarrow - 5 \le 2x - 3 \le 5\) \( \Leftrightarrow - 2 \le 2x \le 8\)\( \Leftrightarrow - 1 \le x \le 4\) Lại có: \(x \in \mathbb{Z} \Rightarrow x \in \left\{ { - 1;\,\,0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}.\) Chọn C. Nguồn: Sưu tầm HocTot.XYZ
|