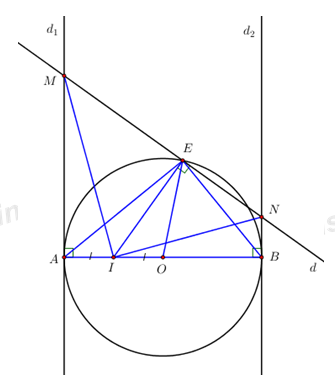
Đề số 39 - Đề thi vào lớp 10 môn ToánĐề thi vào lớp 10 môn Toán - Đề số 39 có đáp án và lời giải chi tiết Đề bài Câu I: (2,0 điểm) 1) Giải phương trình: \({x^2} + 8x + 7 = 0\) 2) Giải hệ phương trình: \(\left\{ \begin{array}{l}2x - y = - 6\\5x + y = 20\end{array} \right.\) Câu II: (2,0 điểm) Cho biểu thức \(A = \dfrac{{\sqrt x + 1}}{{x + 4\sqrt x + 4}}:\left( {\dfrac{x}{{x + 2\sqrt x }} + \dfrac{x}{{\sqrt x + 2}}} \right),\) với \(x > 0\) 1. Rút gọn biểu thức A. 2. Tìm tất cả các giá trị của x để \(A \ge \dfrac{1}{{3\sqrt x }}\) Câu III: (2,0 điểm) 1. Cho đường thẳng \(\left( d \right):\,\,y = ax + b\) . Tìm \(a,b\) để đường thẳng (d) song song với đường thẳng \(\left( {d'} \right):\,\,y = 2x + 3\) và đi qua điểm \(A\left( {1; - 1} \right)\) 2. Cho phương trình \({x^2} - \left( {m - 2} \right)x - 3 = 0\) (m là tham số). Chứng minh phương trình luôn có hai nghiệm phân biệt \({x_1};{x_2}\) với mọi m. Tìm m để các nghiệm đó thỏa mãn hệ thức: \(\sqrt {x_1^2 + 2018} - {x_1} = \sqrt {x_2^2 + 2018} + {x_2}\) Bài IV: (3,0 điểm) Cho đường tròn tâm \(\left( O \right)\), đường kính \(AB = 2R\). Gọi \({d_1};{d_2}\) lần lượt là các tiếp tuyến của đường tròn \(\left( O \right)\) tại A và B, I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn \(\left( O \right)\) sao cho E không trùng với A và B. Đường thẳng d đi qua E và vuông góc với đường thẳng EI cắt \({d_1};{d_2}\) lần lượt tại M, N. 1. Chứng minh AMEI là tứ giác nội tiếp. 2. Chứng minh \(IB.NE = 3IE.NB\) 3. Khi điểm E thay đổi, chứng minh tích \(AM.BN\) có giá trị không đổi và tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R. Câu V: (1,0 điểm) Cho \(a,b,c\) là các số thực dương thỏa mãn: \(a + b + c = 1\) . Chứng minh \(\dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{abc}} \ge 30.\) Lời giải chi tiết Câu I. 1) Giải phương trình: \({x^2} + 8x + 7 = 0\) Ta có: \(a - b + c = 1 - 8 + 7 = 0\) nên phương trình đã cho luôn có một nghiệm là \(x = - 1\) và nghiệm còn lại là: \(x = - \dfrac{c}{a} = - 7\) Vậy tập nghiệm của phương trình là \(S = \left\{ { - 1; - 7} \right\}\). 2) Giải hệ phương trình: \(\left\{ \begin{array}{l}2x - y = - 6\\5x + y = 20\end{array} \right.\) \(\left\{ \begin{array}{l}2x - y = - 6\\5x + y = 20\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = 14\\y = 20 - 5x\end{array} \right.\) \(\Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 20 - 5.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 10\end{array} \right.\) Vậy hệ phương trình đã cho có nghiệm là: \(\left( {x;y} \right) = \left( {2;10} \right)\) Câu II. Cho biểu thức \(A = \dfrac{{\sqrt x + 1}}{{x + 4\sqrt x + 4}}:\left( {\dfrac{x}{{x + 2\sqrt x }} + \dfrac{x}{{\sqrt x + 2}}} \right),\) với \(x > 0\) 1. Rút gọn biểu thức A. \(\begin{array}{l}A = \dfrac{{\sqrt x + 1}}{{x + 4\sqrt x + 4}}:\left( {\dfrac{x}{{x + 2\sqrt x }} + \dfrac{x}{{\sqrt x + 2}}} \right)\\ = \dfrac{{\sqrt x + 1}}{{{{\left( {\sqrt x + 2} \right)}^2}}}:\left( {\dfrac{x}{{\sqrt x \left( {\sqrt x + 2} \right)}} + \dfrac{x}{{\sqrt x + 2}}} \right)\\ = \dfrac{{\sqrt x + 1}}{{{{\left( {\sqrt x + 2} \right)}^2}}}:\left( {\dfrac{{\sqrt x }}{{\sqrt x + 2}} + \dfrac{x}{{\sqrt x + 2}}} \right)\\ = \dfrac{{\sqrt x + 1}}{{{{\left( {\sqrt x + 2} \right)}^2}}}.\dfrac{{\sqrt x + 2}}{{\sqrt x \left( {\sqrt x + 1} \right)}}\\ = \dfrac{1}{{\sqrt x \left( {\sqrt x + 2} \right)}}\end{array}\) Vậy với \(x > 0\) thì \(\) 2. Tìm tất cả các giá trị của x để \(A \ge \dfrac{1}{{3\sqrt x }}\) \(\begin{array}{l}A \ge \dfrac{1}{{3\sqrt x }} \Leftrightarrow \dfrac{1}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge \dfrac{1}{{3\sqrt x }}\\ \Leftrightarrow \dfrac{{3 - \left( {\sqrt x + 2} \right)}}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge 0\\ \Leftrightarrow \dfrac{{1 - \sqrt x }}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge 0\end{array}\) Với \(x > 0\) ta có: \(\sqrt x \left( {\sqrt x + 2} \right) > 0\) khi đó \(\dfrac{{1 - \sqrt x }}{{\sqrt x \left( {\sqrt x + 2} \right)}} \ge 0 \) \(\Leftrightarrow 1 - \sqrt x \ge 0 \Leftrightarrow x \le 1\) Kết hợp với điều kiện ta được: \(0 < x \le 1\) thỏa mãn yêu cầu bài toán. Câu III. 1. Cho đường thẳng \(\left( d \right):\,\,y = ax + b\) . Tìm \(a,b\) để đường thẳng (d) song song với đường thẳng \(\left( {d'} \right):\,\,y = 2x + 3\) và đi qua điểm \(A\left( {1; - 1} \right)\) Đường thẳng (d) song song với đường thẳng (d’) khi và chỉ khi: \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b \ne 3\end{array} \right.\) Khi đó (d) trở thành: \(y = 2x + b\left( {b \ne 3} \right)\) Đường thẳng (d’) đi qua điểm \(A\left( {1; - 1} \right)\) nên ta có: \( - 1 = 2.1 + b \Leftrightarrow b = - 3\left( {tm} \right)\) Vậy đường thẳng (d) cần tìm là: \(y = 2x - 3\) 2. Cho phương trình \({x^2} - \left( {m - 2} \right)x - 3 = 0\) (m là tham số). Chứng minh phương trình luôn có hai nghiệm phân biệt \({x_1};{x_2}\) với mọi m. Tìm m để các nghiệm đó thỏa mãn hệ thức: \(\sqrt {x_1^2 + 2018} - {x_1} = \sqrt {x_2^2 + 2018} + {x_2}\) Xét biệt thức \(\Delta = {\left( {m - 2} \right)^2} + 12 \ge 12 > 0,\forall m\) Vậy phương trình \({x^2} - \left( {m - 2} \right)x - 3 = 0\) luôn có hai nghiệm phân biệt \({x_1};{x_2}\) với mọi m. Giả sử \({x_1} > {x_2}\) Theo hệ thức Viet ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m - 2\\{x_1}{x_2} = - 3\end{array} \right.\) Theo đề ra ta có: \(\begin{array}{l}\sqrt {x_1^2 + 2018} - {x_1} = \sqrt {x_2^2 + 2018} + {x_2}\\ \Leftrightarrow \sqrt {x_1^2 + 2018} - \sqrt {x_2^2 + 2018} = {x_1} + {x_2}\\ \Leftrightarrow x_1^2 + 2018 + x_2^2 + 2018 - 2\sqrt {\left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right)} = x_1^2 + x_2^2 + 2{x_1}{x_2}\\\,\,\left( {Do\,\,{x_1} - {x_2} > 0} \right)\\ \Leftrightarrow 4036 - 2\sqrt {\left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right)} = 2{x_1}{x_2}\\ \Leftrightarrow \sqrt {\left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right)} = 2018 - {x_1}{x_2}\\ \Leftrightarrow \left( {x_1^2 + 2018} \right).\left( {x_2^2 + 2018} \right) = {2018^2} - 4036{x_1}{x_2} + x_1^2x_2^2\\ \Leftrightarrow x_1^2x_2^2 + 2018\left( {x_1^2 + x_2^2} \right) + {2018^2} = {2018^2} - 4036{x_1}{x_2} + x_1^2x_2^2\\ \Leftrightarrow \left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] = - 2{x_1}{x_2}\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} = 0\\ \Leftrightarrow {\left( {m - 2} \right)^2} = 0\\ \Leftrightarrow m = 2\end{array}\) Vậy m = 2 thỏa mãn yêu cầu bài toán. Bài IV. Cho đường tròn tâm \(\left( O \right)\), đường kính \(AB = 2R\). Gọi \({d_1};{d_2}\) lần lượt là các tiếp tuyến của đường tròn \(\left( O \right)\) tại A và B, I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn \(\left( O \right)\) sao cho E không trùng với A và B. Đường thẳng d đi qua E và vuông góc với đường thẳng EI cắt \({d_1};{d_2}\) lần lượt tại M, N.
1. Chứng minh AMEI là tứ giác nội tiếp. Ta có: MA là tiếp tuyến của (O) tại A nên \(\angle IAM = {90^0}\) Xét tứ giác \(AMEI\) có \(\angle IAM + \angle IEM = {90^0} + {90^0} = {180^0}\) \( \Rightarrow \) Tứ giác \(AMEI\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800) 2. Chứng minh \(IB.NE = 3IE.NB\) Ta có \(\angle IEA + \angle IEB = \angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn); \(\angle NEB + \angle IEB = \angle NEI = {90^0}\,\,\left( {gt} \right)\); \( \Rightarrow \angle IEA = \angle NEB\) Xét \(\Delta IEA\) và \(\Delta NEB\) có: \(\angle IEA = \angle NEB\,\,\left( {cmt} \right)\); \(\angle IAE = \angle BAE = \angle NBE\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BE); \( \Rightarrow \Delta IEA \sim \Delta NEB\,\,\left( {g.g} \right) \) \(\Rightarrow \dfrac{{IE}}{{IA}} = \dfrac{{NE}}{{NB}}\) \(\Rightarrow IA.NE = IE.NB\) \(\Rightarrow 3IA.NE = 3IE.NB\) Do I là trung điểm của OA \( \Rightarrow IA = \dfrac{1}{2}OA = \dfrac{1}{2}.\dfrac{1}{2}AB = \dfrac{1}{4}AB \) \(\Rightarrow IA = \dfrac{1}{3}IB\) hay \(IB = 3IA\). \( \Rightarrow IB.NE = 3IE.NB\,\,\left( {dpcm} \right)\). 3. Khi điểm E thay đổi chứng minh tích \(AM.BN\) có giá trị không đổi và tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R. +) Chứng minh tích \(AM.BN\) có giá trị không đổi Xét tứ giác \(BNEI\) có \(\angle IBN + \angle IEN = {90^0} + {90^0} = {180^0}\) \( \Rightarrow \) Tứ giác \(BNEI\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800) \( \Rightarrow \angle NEB = \angle NIB\) (hai góc nội tiếp cùng chắn cung NB) Ta có \(\angle AMI = \angle AEI\) (hai góc nội tiếp cùng chắn cung AI) ; Mà \(\angle AEI = \angle NEB\,\,\left( {cmt} \right)\) \( \Rightarrow \angle AMI = \angle NIB\). Xét \(\Delta AMI\) và \(\Delta BIN\) có: \(\begin{array}{l}\angle AMI = \angle NIB\,\,\left( {cmt} \right);\\\angle MAI = \angle IBN = {90^0}\,\,\left( {gt} \right);\\ \Rightarrow \Delta AMI \sim \Delta BIN\,\,\left( {g.g} \right)\\ \Rightarrow \dfrac{{AM}}{{BI}} = \dfrac{{AI}}{{BN}}\\ \Rightarrow AM.BN = AI.BI\end{array}\) Ta có \(AI = \dfrac{1}{4}AB = \dfrac{1}{4}.2R = \dfrac{R}{2};\) \(BI = \dfrac{3}{4}AB = \dfrac{3}{4}.2R = \dfrac{{3R}}{2}\) \( \Rightarrow AM.BN = \dfrac{R}{2}.\dfrac{{3R}}{2} = \dfrac{{3{R^2}}}{4} = const\). +) Tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R. Tứ giác BNEI là tứ giác nội tiếp (cmt) \( \Rightarrow \angle ENI = \angle EBI\) (hai góc nội tiếp cùng chắn cung EI) Do tứ giác \(AMEI\) nội tiếp (cmt) \( \Rightarrow \angle IME = \angle IAE\) (hai góc nội tiếp cùng chắn cung IE) \( \Rightarrow \angle ENI = \angle IME = \angle EBI + \angle IAE = {90^0}\) (\(\Delta ABE\) vuông tại E) \( \Rightarrow \angle MIN = {90^0} \Rightarrow \Delta IMN\) vuông tại I \( \Rightarrow {S_{IMN}} = \dfrac{1}{2}IM.IN\) Đặt \(\angle AIM = \alpha \) \( \Rightarrow \angle BNI = \alpha \,\,\left( {{0^0} < \alpha < {{90}^0}} \right)\) \(\left( {Do\,\,\Delta AMI \sim \Delta BIN} \right)\). Xét tam giác vuông AIM có \(\cos \angle AIM = \cos \alpha = \dfrac{{AI}}{{MI}}\) \(\Rightarrow MI = \dfrac{{AI}}{{\cos \alpha }} = \dfrac{{\dfrac{R}{2}}}{{\cos \alpha }} = \dfrac{R}{{2\cos \alpha }}\) Xét tam giác vuông BIN có : \(\sin \angle BNI = \sin \alpha = \dfrac{{BI}}{{IN}}\) \( \Rightarrow IN = \dfrac{{BI}}{{\sin \alpha }} = \dfrac{{\dfrac{{3R}}{2}}}{{\sin \alpha }} = \dfrac{{3R}}{{2\sin \alpha }}\) \( \Rightarrow {S_{IMN}} = \dfrac{1}{2}IM.IN = \dfrac{1}{2}.\dfrac{R}{{2\cos \alpha }}.\dfrac{{3R}}{{2\sin \alpha }} = \dfrac{{3{R^2}}}{{8\sin \alpha \cos \alpha }}\) Do \({0^0} < \alpha < {90^0}\) \( \Rightarrow \sin \alpha > 0,\,\,\cos \alpha > 0\) và \(\cos \alpha = \sqrt {1 - {{\sin }^2}\alpha } \). \(\begin{array}{l} \Rightarrow \sin \alpha .\cos \alpha = \sin \alpha .\sqrt {1 - {{\sin }^2}\alpha } \mathop \le \limits^{Cauchy} \dfrac{{{{\sin }^2}\alpha + 1 - {{\sin }^2}\alpha }}{2} = \dfrac{1}{2}\\ \Rightarrow {S_{IMN}} \ge \dfrac{{3{R^2}}}{{8.\dfrac{1}{2}}} = \dfrac{{3{R^2}}}{4}\end{array}\) Dấu bằng xảy ra \( \Leftrightarrow \sin \alpha = \sqrt {1 - {{\sin }^2}\alpha }\) \( \Leftrightarrow 2{\sin ^2}\alpha = 1 \) \(\Leftrightarrow \sin \alpha = \dfrac{1}{{\sqrt 2 }} \Leftrightarrow \alpha = {45^0}\) Vậy \({S_{IMN\,\,\min }} = \dfrac{{3{R^2}}}{4} \Leftrightarrow \angle AIM = {45^0}\) Câu V. Ta có: \(\begin{array}{l}\dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{abc}} = \dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{9abc}} + \dfrac{8}{{9abc}}\\ \ge \dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{3{{\left( {bc + ac + ab} \right)}^2}}} + \dfrac{8}{{9\dfrac{{{{\left( {a + b + c} \right)}^3}}}{{27}}}}\\ \ge 2\sqrt {\dfrac{1}{{{a^2} + {b^2} + {c^2}}}.\dfrac{1}{{3{{\left( {bc + ac + ab} \right)}^2}}}} + 24\\ \ge 2\sqrt {\dfrac{1}{{3\dfrac{{{{\left( {{a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ac} \right)}^2}}}{{27}}}}} + 24 = 30\end{array}\) HocTot.XYZ
|