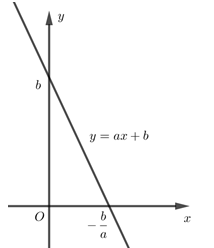
Đề số 6 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10Đáp án và lời giải chi tiết Đề số 6 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 10 Đề bài PHẦN 1. PHẦN TRẮC NGHIỆM (3,0 điểm) Chọn đáp án đúng trong mỗi câu sau: Câu 1 (NB). Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 - 5t\end{array} \right.\,\,\,\,\left( {t \in \mathbb{R}} \right)\) A. \(\overrightarrow u = \left( {3;\,1} \right)\). B. \(\overrightarrow u = \left( { - 5;\,\,2} \right)\). C. \(\overrightarrow u = \left( {1;\,3} \right).\) D. \(\overrightarrow u = \left( {2;\, - 5} \right).\) Câu 2 (TH). Trong mặt phẳng tọa độ Oxy, cho đường elip \(\left( E \right):\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{2^2}}} = 1\) có 2 tiêu điểm là \({F_1},{F_2}\). M là điểm thuộc elip \(\left( E \right)\). Giá trị của biểu thức \(M{F_1} + M{F_2}\) bằng: A. \(5\). B. \(6.\) C. \(3.\) D. \(2.\). Câu 3 (TH). Cho \(\pi < \alpha < \frac{{3\pi }}{2}\). Phát biểu nào sau đây là đúng? A. \(\sin \alpha < 0,\cos \alpha < 0.\) B. \(\sin \alpha < 0,\cos \alpha > 0.\) C. \(\sin \alpha > 0,\cos \alpha < 0.\) D. \(\sin \alpha > 0,\cos \alpha > 0.\) Câu 4 (TH). Tập nghiệm của bất phương trình \({x^2} - 7x + 6 > 0\) là: A. \(\left( { - \infty ;1} \right) \cap \left( {6; + \infty } \right).\) B. \(\left( { - 6, - 1} \right).\) C. \(\left( {1;6} \right).\) D. \(\left( { - \infty ;1} \right) \cup \left( {6; + \infty } \right).\) Câu 5 (VD). Biểu thức \(\frac{1}{2}\sin \alpha + \frac{{\sqrt 3 }}{2}\cos \alpha \) bằng A. \(\cos \left( {\alpha - \frac{\pi }{3}} \right).\) B. \(\sin \left( {\alpha + \frac{\pi }{3}} \right).\) C. \(\cos \left( {\alpha + \frac{\pi }{3}} \right).\) D. \(\sin \left( {\alpha - \frac{\pi }{3}} \right).\) Câu 6 (NB). Biểu thức \(\sin \left( { - \alpha } \right)\) bằng A. \( - \sin \alpha .\) B. \(\sin \alpha .\) C. \(\cos \alpha .\) D. \( - \cos \alpha .\) Câu 7 (TH). Trong mặt phẳng tọa độ Oxy, tâm của đường tròn \(\left( C \right):{x^2} + {y^2} - 4x + 6y - 1 = 0\) có tọa độ là: A. \(\left( {2;\,3} \right).\) B. \(\left( {2; - 3} \right).\) C. \(\left( { - 2;\,3} \right).\) D. \(\left( { - 2; - 3} \right).\) Câu 8 (VD). Cho đồ thị của hàm số \(y = ax + b\) có đồ thị là hình bên. Tập nghiệm của bất phương trình \(ax + b > 0\) là:
A. \(\left( { - \frac{b}{a}; + \infty } \right).\) B. \(\left( { - \infty ;\frac{b}{a}} \right).\) C. \(\left( { - \infty ; - \frac{b}{a}} \right).\) D. \(\left( {\frac{b}{a}; + \infty } \right).\) Câu 9 (TH). Vectơ nào sau đây không là vectơ pháp tuyến của đường thẳng \(2x - 4y + 1 = 0\) ? A. \(\overrightarrow n = \left( {1; - 2} \right).\) B. \(\overrightarrow n = \left( {2; - 4} \right).\) C. \(\overrightarrow n = \left( {2;4} \right).\) D. \(\overrightarrow n = \left( { - 1;2} \right).\) Câu 10 (TH). Biểu thức \(\cos \left( {\alpha + 2\pi } \right)\) bằng: A. \( - \sin \alpha .\) B. \(\sin \alpha .\) C. \(\cos \alpha .\) D. \( - \cos \alpha .\) Câu 11 (VD). Tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - 6 < 0\\3x + 15 > 0\end{array} \right.\) là: A. \(\left( { - 5; - 3} \right).\) B. \(\left( { - 3;5} \right).\) C. \(\left( {3;5} \right).\) D. \(\left( { - 5;3} \right).\) Câu 12 (NB). Số giầy bán được trong một quý của một cửa hàng bán giầy được thống kê trong bảng sau đây
Mốt của bảng trên là: A. \(39.\) B. \(93.\) C. \(639.\) D. \(35.\) PHẦN 2. PHẦN TỰ LUẬN ( 5 điểm) Câu 1 (VD) (3,5 điểm). 1) Tìm m thỏa mãn bất phương trình \({x^2} + 2mx - m + 2 > 0\) nghiệm đúng với \(\forall x \in \mathbb{R}\). 2) Giải bất phương trình \(\sqrt {x + 9} < x + 3\) 3) Cho các góc \(\alpha ,\beta \) thỏa mãn \(0 < \alpha < \frac{\pi }{2} < \beta < \pi \) và \(\sin \alpha = \frac{1}{3},\sin \beta = \frac{2}{3}\). Tính \(\sin \left( {\alpha + \beta } \right)\) Câu 2 (VD) (3,0 điểm). 1) Trong mặt phẳng tọa độ Oxy, cho hai điểm \(A\left( { - 1;2} \right)\) và \(B\left( {1;5} \right)\). Lập phương trình tham số và phương trình tổng quát của đường thẳng AB. 2) Trong mặt phẳng tọa độ Oxy, cho điểm \(I\left( {2;3} \right)\) và đường thẳng \(\Delta :3x - 4y - 4 = 0\). Tính khoảng cách từ điểm I đến đường thẳng \(\Delta \) và lập phương trình đường tròn tâm I tiếp xúc với đường thẳng \(\Delta \). 3) Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng \({\Delta _1}:x - y - 1 = 0\) và \({\Delta _2}:x + my + 2 = 0\). Xác định giá trị của m biết rằng góc giữa hai đường thẳng đã cho bằng \({45^o}\). Câu 3 (VDC) (0,5 điểm). Cho x thỏa mãn \({\left( {{{\cos }^4}x - {{\sin }^4}x} \right)^2} = \frac{1}{3}\). Tính giá trị của biểu thức \(\cos 8x\). Lời giải chi tiết PHẦN 1. PHẦN TRẮC NGHIỆM
Câu 1: Phương pháp: Đường thẳng \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\) nhận \(\overrightarrow u = \left( {a;\,b} \right)\) làm VTCP Cách giải: Vectơ \(\overrightarrow u = \left( {2; - 5} \right)\) là một vectơ chỉ phương của đường thẳng \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 - 5t\end{array} \right.\,\,\,\,\left( {t \in \mathbb{R}} \right)\) Chọn D. Câu 2: Phương pháp: Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có 2 tiêu điểm là \({F_1},{F_2}\) là tập hợp các điểm M sao cho \(M{F_1} + M{F_2} = 2a\) Cách giải: Ta có: \(M{F_1} + M{F_2} = 2a = 2.3 = 6.\) Chọn B. Câu 3: Phương pháp: Dựa vào đường tròn đơn vị. Cách giải: Với \(\pi < \alpha < \frac{{3\pi }}{2} \Rightarrow \) Điểm biểu diễn góc \(\alpha \) thuộc góc phần tư thứ III \( \Rightarrow \sin \alpha < 0,\cos \alpha < 0\) Chọn A. Câu 4: Phương pháp: Sử dụng quy tắc xét dấu của tam thức bậc hai: Trong trái, ngoài cùng. Cách giải: \(\begin{array}{l}{x^2} - 7x + 6 > 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 6} \right) > 0\\ \Leftrightarrow \left[ \begin{array}{l}x > 6\\x < 1\end{array} \right.\end{array}\) Vậy tập nghiệm của BPT là \(\left( { - \infty ;1} \right) \cup \left( {6; + \infty } \right).\) Chọn D. Câu 5: Phương pháp: Sử dụng công thức: \(\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b.\) Cách giải: Ta có: \(\begin{array}{l}\frac{1}{2}\sin \alpha + \frac{{\sqrt 3 }}{2}\cos \alpha \\ = \sin \alpha .\cos \frac{\pi }{3} + \cos \alpha .\sin \frac{\pi }{3}\\ = \sin \left( {\alpha + \frac{\pi }{3}} \right)\end{array}\) Chọn B. Câu 6: Phương pháp: Cos đối, sin bù, phụ chéo, khác pi tan. Cách giải: Ta có: \(\sin \left( { - \alpha } \right) = - \sin \alpha \) Chọn A. Câu 7: Phương pháp: Phương trình đường tròn \({x^2} + {y^2} - 2ax - 2by + c = 0\) có tâm \(I\left( {a;\,b} \right)\) Cách giải: Đường tròn \(\left( C \right):{x^2} + {y^2} - 4x + 6y - 1 = 0\) có tâm \(I\left( {2; - 3} \right)\) Chọn B. Câu 8: Phương pháp: Nhìn đồ thị xét dấu của a,b từ đó áp dụng quy tắc xét dấu của nhị thức bậc nhất: “Phải cùng, trái khác”. Cách giải: Dựa vào đồ thị hàm số ta thấy đồ thị hàm số cắt trục Oy tại một điểm có tung độ dương \( \Rightarrow b > 0.\) Và đồ thị hàm số cắt trục hoành tại điểm có hoành độ dương \( \Rightarrow - \frac{b}{a} > 0 \Leftrightarrow \frac{b}{a} < 0 \Leftrightarrow a < 0.\) \( \Rightarrow ax + b > 0 \Leftrightarrow ax > - b \Leftrightarrow x < \frac{{ - b}}{a}.\) Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - \frac{b}{a}} \right).\) Chọn C. Câu 9: Phương pháp: Đường thẳng \(ax + by + c = 0\) nhận \(\overrightarrow n = \left( {a,b} \right)\) làm VTPT. \(\overrightarrow n = k\overrightarrow {n'} \) thì \(\overrightarrow n //\overrightarrow {n'} \) Cách giải: Đường thẳng \(2x - 4y + 1 = 0\) nhận \(\overrightarrow {{n_1}} = \left( {2; - 4} \right)\) làm VTPT \(\begin{array}{l} Do đó các véc tơ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} ,\overrightarrow {{n_3}} \) đều là VTPT của đường thẳng. Vậy chỉ có vecto \(\overrightarrow n = \left( {2;\,4} \right)\) không là VTPT của đường thẳng đã cho. Chọn C. Câu 10: Phương pháp: Góc quét một số chẵn lần \(\pi \) sẽ trở về điểm ban đầu. Cách giải: Ta có: \(\cos \left( {\alpha + 2\pi } \right) = \cos \alpha \) Chọn C. Câu 11: Phương pháp: Giải từng BPT sau đó kết hợp nghiệm của hệ. Cách giải: \(\left\{ \begin{array}{l}2x - 6 < 0\\3x + 15 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 3\\x > - 5\end{array} \right.\)\( \Leftrightarrow - 5 < x < 3\) Tập nghiệm của bất phương trình là \(\left( { - 5;3} \right).\) Chọn D. Câu 12: Phương pháp: Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng tần số. Cách giải: Dựa vào bảng số liệu ta thấy Mốt là 39. Chọn A. PHẦN 2. PHẦN TỰ LUẬN Câu 1. Phương pháp: 1) Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\) - Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta = 0\)thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\,{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\,{x_2}} \right).\) 2) \(\sqrt {f\left( x \right)} < g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) > 0\\f\left( x \right) < {g^2}\left( x \right)\end{array} \right.\) 3) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) để tính \(\cos \alpha ,\cos \beta \), từ đó tính \(\sin \left( {\alpha + \beta } \right)\) bằng công thức cộng. Cách giải: 1) Tìm m thỏa mãn bất phương trình \({x^2} + 2mx - m + 2 > 0\) nghiệm đúng với \(\forall x \in \mathbb{R}\). Ta có: \(\Delta ' = {m^2} + m - 2\) Bất phương trình \({x^2} + 2mx - m + 2 > 0\) nghiệm đúng với mọi \(x \in \mathbb{R}\). \(\begin{array}{l} \Leftrightarrow \Delta ' < 0\\ \Leftrightarrow {m^2} + m - 2 < 0\\ \Leftrightarrow \left( {m + 2} \right)\left( {m - 1} \right) < 0\\ \Leftrightarrow - 2 < m < 1\end{array}\) Vậy với \( - 2 < m < 1\) thỏa mãn yêu cầu đề bài. 2) Giải bất phương trình \(\sqrt {x + 9} < x + 3\) \(\begin{array}{l}\sqrt {x + 9} < x + 3\\ \Leftrightarrow \left\{ \begin{array}{l}x + 9 \ge 0\\x + 3 > 0\\x + 9 < {x^2} + 6x + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 9\\x > - 3\\{x^2} + 5x > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > - 3\\\left[ \begin{array}{l}x > 0\\x < - 5\end{array} \right.\end{array} \right. \Leftrightarrow x > 0\end{array}\) Vậy tập nghiệm của BPT là \(\left( {0; + \infty } \right).\) 3) Cho các góc \(\alpha ,\beta \) thỏa mãn \(0 < \alpha < \frac{\pi }{2} < \beta < \pi \) và \(\sin \alpha = \frac{1}{3},\sin \beta = \frac{2}{3}\). Tính \(\sin \left( {\alpha + \beta } \right)\) Ta có \(\sin \alpha = \frac{1}{3} \Rightarrow {\sin ^2}\alpha = \frac{1}{9}\) \( \Rightarrow {\cos ^2}\alpha = 1 - \frac{1}{9} = \frac{8}{9}\) Do \(0 < \alpha < \frac{\pi }{2}\) \( \Rightarrow \cos \alpha > 0\) \( \Rightarrow \cos \alpha = \frac{{2\sqrt 2 }}{3}\) Ta có \(\sin \beta = \frac{2}{3} \Rightarrow {\sin ^2}\beta = \frac{4}{9}\) \( \Rightarrow {\cos ^2}\beta = 1 - \frac{4}{9} = \frac{5}{9}\) Do \(\frac{\pi }{2} < \beta < \pi \) \( \Rightarrow \cos \beta < 0 \Rightarrow \cos \beta = - \frac{{\sqrt 5 }}{3}\) Vậy \(\begin{array}{l}\sin \left( {\alpha + \beta } \right)\\ = \sin \alpha \cos \beta + \cos \alpha \sin \beta \\ = \frac{1}{3}.\left( { - \frac{{\sqrt 5 }}{3}} \right) + \frac{{2\sqrt 2 }}{3}.\frac{2}{3}\\ = \frac{{4\sqrt 2 - \sqrt 5 }}{9}\end{array}\) Câu 2. Phương pháp: 1) Xác định VTCP để viết phương trình tham số, VTPT để viết phương trình tổng quát 2) Cho đường thẳng \(\Delta :ax + by + c = 0\) và điểm \({M_0}\left( {{x_0};{y_0}} \right)\) \( \Rightarrow {d_{\left( {{M_0};\Delta } \right)}} = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) Đường thẳng \(\Delta \) là tiếp tuyến của đường tròn \(\left( {O,R} \right) \Leftrightarrow d\left( {O,\Delta } \right) = R\) Phương trình đường tròn tâm \(I\left( {a;\,b} \right),\,\,\) bán kính \(R:\,\,{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}.\) 3) Góc giữa hai đường thẳng bằng góc giữa 2 VTPT (VTCP) của 2 đường thẳng đó \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \frac{{\left| {\overrightarrow a .\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\) Cách giải: 1) Trong mặt phẳng tọa độ Oxy, cho hai điểm \(A\left( { - 1;2} \right)\) và \(B\left( {1;5} \right)\). Lập phương trình tham số và phương trình tổng quát của đường thẳng AB. Ta có: \(\overrightarrow {AB} = \left( {2;3} \right)\) là một VTCP của đường thẳng AB. \( \Rightarrow \overrightarrow n = \left( {3; - 2} \right)\) là một VTPT của đường thẳng AB. Ta có: \(A\left( { - 1;2} \right) \in AB\) \( \Rightarrow \) Phương trình tham số của đường thẳng AB: \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 + 3t\end{array} \right.\,\,\,\,\left( {t \in \mathbb{R}} \right)\) Phương trình tổng quát của đường thẳng AB: \(3\left( {x + 1} \right) - 2\left( {y - 2} \right) = 0\) \( \Leftrightarrow 3x - 2y + 7 = 0\) 2) Trong mặt phẳng tọa độ Oxy, cho điểm \(I\left( {2;3} \right)\) và đường thẳng \(\Delta :3x - 4y - 4 = 0\). Tính khoảng cách từ điểm I đến đường thẳng \(\Delta \) và lập phương trình đường tròn tâm I tiếp xúc với đường thẳng \(\Delta \). Ta có: \(d\left( {I,\Delta } \right) = \frac{{\left| {3.2 - 4.3 - 4} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{10}}{5} = 2\) Đường thẳng \(\Delta \) tiếp xúc đường tròn \(\left( {I,R} \right) \Leftrightarrow R = d\left( {I,\Delta } \right) = 2\) Vậy phương trình đường tròn cần tìm là \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 4.\) 3) Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng \({\Delta _1}:x - y - 1 = 0\) và \({\Delta _2}:x + my + 2 = 0\). Xác định giá trị của m biết rằng góc giữa hai đường thẳng đã cho bằng \({45^o}\). Ta có: \({\Delta _1}\) nhận \(\overrightarrow {{n_1}} = \left( {1; - 1} \right)\) là một VTPT \({\Delta _2}\) nhận \(\overrightarrow {{n_2}} = \left( {1;m} \right)\) là một VTPT Góc giữa hai đường thẳng đã cho bằng \({45^o}\)\( \Leftrightarrow \) \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos {45^o} = \frac{{\sqrt 2 }}{2}\) \(\begin{array}{l}\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \frac{{\left| {1.1 + \left( { - 1} \right).m} \right|}}{{\sqrt {1 + 1} .\sqrt {1 + {m^2}} }} = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \frac{{\left| {1 - m} \right|}}{{\sqrt 2 .\sqrt {1 + {m^2}} }} = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \left| {1 - m} \right| = \sqrt {1 + {m^2}} \\ \Leftrightarrow 1 - 2m + {m^2} = 1 + {m^2}\\ \Leftrightarrow 2m = 0 \Leftrightarrow m = 0.\end{array}\) Vậy với \(m = 0\) thỏa mãn yêu cầu đề bài. Câu 3. Phương pháp: Từ dữ kiện đề bài tính \(\cos 2x\) từ đó áp dụng công thức góc nhân đôi để tính \(\cos 8x\) Cách giải: Cho x thỏa mãn \({\left( {{{\cos }^4}x - {{\sin }^4}x} \right)^2} = \frac{1}{3}\). Tính giá trị của biểu thức \(\cos 8x\). Ta có: \(\begin{array}{l}\frac{1}{3} = {\left( {{{\cos }^4}x - {{\sin }^4}x} \right)^2}\\ = {\left[ {\left( {{{\cos }^2}x - {{\sin }^2}x} \right)\left( {{{\cos }^2}x + {{\sin }^2}x} \right)} \right]^2}\\ = {\left( {\cos 2x.1} \right)^2}\\ = {\cos ^2}2x\\ \Rightarrow {\cos ^2}2x = \frac{1}{3}\end{array}\) \(\begin{array}{l}\cos 8x = 2{\cos ^2}4x - 1\\ = 2{\left( {2{{\cos }^2}2x - 1} \right)^2} - 1\\ = 2{\left( {2.\frac{1}{3} - 1} \right)^2} - 1\\ = 2{\left( { - \frac{1}{3}} \right)^2} - 1 = - \frac{7}{9}\end{array}\) Vậy \(\cos 8x = - \frac{7}{9}.\) Nguồn: Sưu tầm HocTot.XYZ
|