Đề số 7 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10Đáp án và lời giải chi tiết Đề số 7 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 10 Đề bài PHẦN 1 – TRẮC NGHIỆM (6 điểm) Câu 1: (VD) Giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{x}{2} + \frac{2}{{x - 1}}\) với \(x\; > \;1\) là: A. \(2\sqrt 2 \) B. \(\;2\) C. \(\frac{5}{2}\) D. 4 Câu 2: (VD) Số nghiệm nguyên của hệ bất phương trình \(\left\{ \begin{array}{l}2x + 1 > 3x - 2\\ - x - 3 < 0\end{array} \right.\) là: A. \(9\) B. \(7\) C. \(5\) D. vô số Câu 3: (VD) Khoảng cách từ điểm \(M\left( {0;1} \right)\) đến đường thẳng \(\Delta :5x - 12y - 1 = 0\) là: A. \(\sqrt {13} \) B. \(1\) C. \(3\) D. \(\frac{{11}}{{13}}\) Câu 4: (NB) Biết \(A,B,C\) là các góc của tam giác \(ABC\), mệnh đề nào sau đây đúng: A. \(\cos \left( {A + C} \right) = \cos B\) B. \(\tan \left( {A + C} \right) = - \tan B\) C. \(\cot \left( {A + C} \right) = \cot B\) D. \(\sin \left( {A + C} \right) = - \sin B\) Câu 5: (VDC) Cho ba điểm \(A\left( { - 6;3} \right)\), \(B\left( {0; - 1} \right)\), \(C\left( {3;2} \right)\). \(M(a;b)\)là điểm nằm trên đường thẳng \(d :2x - y + 3 = 0\) sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) nhỏ nhất. Đẳng thức nào sau đây đúng? A. \(5(a + b) = 28\) B. \(5(a + b) = - 28\) C. \(5(a + b) = 2\) D. \(5(a + b) = - 2\) Câu 6: (TH) Thống kê điểm kiểm tra 15’ môn Toán của một lớp 10 trường THPT M.V. Lômônôxốp được ghi lại như sau:
Số trung vị của mẫu số liệu trên là: A. 8 B. 6 C. 7 D. 9 Câu 7: (VD) Tìm côsin góc giữa \(2\) đường thẳng \({\Delta _1}:x + 2y - 7 = 0\) và \({\Delta _2}:2x - 4y + 9 = 0.\) A. \(\frac{2}{{\sqrt 5 }}\) B. \( - \frac{3}{5}\) C. \( - \frac{2}{{\sqrt 5 }}\) D. \(\frac{3}{5}\) Câu 8: (TH) Cho elip \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\), khẳng định nào sau đây sai ? A. Tiêu cự của elip bằng \(2\) B. Tâm sai của elip là \(e = \frac{1}{5}\) C. Độ dài trục lớn bằng \(2\sqrt 5 \) D. Độ dài trục bé bằng \(4\) Câu 9: (TH) Đường tròn tâm \(I(3; - 1)\) và bán kính \(R = 2\) có phương trình là: A. \({(x + 3)^2} + {(y - 1)^2} = 4\) B. \({(x - 3)^2} + {(y + 1)^2} = 2\) C. \({(x - 3)^2} + {(y + 1)^2} = 4\) D. \({(x + 3)^2} + {(y - 1)^2} = 2\) Câu 10: (VD) Cho hai điểm \(A(1;2),B( - 3;1)\), đường tròn (C) có tâm nằm trên trục Oy và đi qua hai điểm A, B có bán kính bằng: A. \(\sqrt {17} \) B. \(\frac{{\sqrt {85} }}{2}\) C. \(\frac{{85}}{4}\) D. \(17\) Câu 11: (VD) Cho đường tròn \((C):\,\,{(x - 2)^2} + {(y + 3)^2} = 25.\) Phương trình tiếp tuyến của \((C)\) tại điểm \(B\left( { - 1;1} \right)\) là: A. \(x - 2y - 3 = 0\) B. \(3x - 4y - 7 = 0\) C. \(x - 2y + 3 = 0\) D. \(3x-4y + 7 = 0\) Câu 12: (VD) Phương trình tổng quát của đường thẳng đi qua hai điểm \(A\left( {3; - 1} \right)\) và \(B\left( { - 6;2} \right)\)là: A. \(x + 3y = 0\) B. \(x + 3y - 6 = 0\) C. \(3x - y = 0\) D. \(3x - y - 10 = 0\) Câu 13: (VD) Phương trình tham số của đường thẳng qua \(M\left( {-2;3} \right)\) và song song với đường thẳng \(\frac{{x - 7}}{{ - 1}} = \frac{{y + 5}}{5}\) là: A. \(\left\{ \begin{array}{l}x = - 2 - t\\y = 3 + 5t\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = - 1 - 2t\\y = 5 + 3t\end{array} \right.\) C. \(\left\{ \begin{array}{l}x = 3 - t\\y = 2 + 5t\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = 3 + 5t\\y = 2 - t\end{array} \right.\) Câu 14: (TH) Miền nghiệm của bất phương trình \(5\left( {x + 2} \right) - 9 < 2x - 2y + 7\) không chứa điểm nào trong các điểm sau? A. \(\left( {2;3} \right)\) B. \(\left( { - 2;1} \right)\) C. \(\left( {2; - 1} \right)\) D. \(\left( {0;0} \right)\) Câu 15: (VD) Tập nghiệm của bất phương trình \(\frac{{x - 1}}{{x - 3}} > 1\) là: A. \(\emptyset \) B. \(\mathbb{R}\) C. \(\left( {3; + \infty } \right)\) D. \(\left( { - \infty ;5} \right)\) Câu 16: (TH) Giá trị của \(x\) thỏa mãn bất phương trình \(1 - \sqrt {13 + 3{x^2}} > 2x\) là: A. \(x = \frac{3}{2}\) B. \(x = - \frac{3}{2}\) C. \(x = \frac{7}{2}\) D. \(x = - \frac{7}{2}\) Câu 17: (VD) Cho ba số \(a,b,c\)dương. Mệnh đề nào sau đây sai ? A. \(\frac{1}{{1 + {a^2}}} + \frac{1}{{1 + {b^2}}} + \frac{1}{{1 + {c^2}}} \ge \frac{1}{2}\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)\) B. \((1 + 2b)(2b + 3a)(3a + 1) \ge 48ab\) C. \((1 + 2a)(2a + 3b)(3b + 1) \ge 48ab\) D. \(\left( {\frac{a}{b} + 1} \right)\left( {\frac{b}{c} + 1} \right)\left( {\frac{c}{a} + 1} \right) \ge 8\) Câu 18: (VD) Giải bất phương trình\(\left| {2x + 5} \right| \le {x^2} + 2x + 4\) được các giá trị \(x\) thỏa mãn: A. \(x \le - 1\) hoặc \(x \ge 1\) B. \( - 1 \le x \le 1\) C. \(x \le 1\) D. \(x \ge 1\) Câu 19: (TH) Điều tra về số tiền mua đồ dùng học tập trong một tháng của 40 học sinh, ta có mẫu số liệu như sau (đơn vị: nghìn đồng):
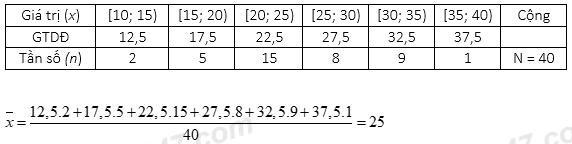
Số trung bình của mẫu số liệu là: A. 22,5 B. 25 C. 25,5 D. 27 Câu 20: (VD) Bất phương trình \(\frac{{x - 1}}{{{x^2} + 4x + 3}} \le 0\) có tập nghiệm là: A. \(\left[ { - 3; - 1} \right] \cup \left[ {1; + \infty } \right)\) B. \(\left( { - \infty ; - 3} \right) \cup \left( { - 1;1} \right]\) C. \(\left( { - \infty ; - 3} \right] \cup \left[ { - 1;1} \right]\) D. \(\left( { - 3; - 1} \right) \cup \left[ {1; + \infty } \right)\) Câu 21: (VD) Cho \(\tan \alpha = 3.\) Giá trị của biểu thức \(A = \frac{{3\sin \alpha + \cos \alpha }}{{\sin \alpha - \cos \alpha }}\) là: A. \(\frac{7}{3}\) B. \(\frac{5}{3}\) C. \(7\) D. \(5\) Câu 22: (VD) Tam thức \(f(x) = {x^2} - 12x - 13\) nhận giá trị âm khi và chỉ khi: A. \(-1 < x < 13\) B.\(-13 < x < 1\) C. \(x < -1\) hoặc \(x > 13\) D. \(x < -13\) hoặc \(x > 1\) Câu 23: (TH) Cặp bất phương trình nào sau đây không tương đương? A. \(\sqrt {x - 1} \ge x\) và \(\left( {2x + 1} \right)\sqrt {x - 1} \ge x\left( {2x + 1} \right)\). B. \(2x - 1 + \frac{1}{{x - 3}} < \frac{1}{{x - 3}}\)và \(2x - 1 < 0\). C. \({x^2}\left( {x + 2} \right) < 0\)và \(x + 2 < 0\). D. \({x^2}\left( {x + 2} \right) > 0\) và \(\left( {x + 2} \right) > 0\) Câu 24: (NB) Cho đường thẳng \(\left( d \right)\) có phương trình tổng quát: \(3x - 2y + 2019 = 0\). Tìm mệnh đề sai trong các mệnh đề sau: A. \(\left( d \right)\)có vectơ pháp tuyến là \(\overrightarrow n = \left( {3; - 2} \right)\) B. \(\left( d \right)\)có vectơ chỉ phương \(\overrightarrow u = \left( {2;3} \right)\) C. \(\left( d \right)\)song song với đường thẳng \(\frac{{x + 5}}{2} = \frac{{y - 1}}{3}\) D. \(\left( d \right)\)có hệ số góc \(k = - 2\) PHẦN 2 – TỰ LUẬN (4 điểm) Học sinh làm bài ra giấy kiểm tra. Bài 1 (VD): (1,0 điểm) Giải bất phương trình: \(\frac{{3{x^2} - 8x - 3}}{{2x - 1}} \ge 0\). Bài 2 (VD): (1,0 điểm) Tìm m để bất phương trình \(3{x^2} + 2\left( {m - 1} \right)x + m + 5 > 0\) có tập nghiệm là \(\mathbb{R}\). Bài 3 (VD): (0,5 điểm) Cho \(\tan \alpha = - \sqrt 5 \,\,\,\,\left( {\frac{\pi }{2} < \alpha < \pi } \right)\), Tính \(\cos \alpha \) và \(\sin 2\alpha \). Bài 4 (VD): (1,5 điểm) Trong hệ tọa độ Oxy, cho điểm\(A\left( {-1;2} \right)\) và đường thẳng \(\Delta :x + 3y + 5 = 0\). a) (0,5 điểm) Viết phương trình đường thẳng d đi qua A và vuông góc với \(\Delta \). b) (0,5 điểm) Viết phương trình đường tròn tâm \(A\left( {-1;2} \right)\) và tiếp xúc với \(\Delta \). c) (0,5 điểm) Tìm điểm M trên đường thẳng \(\Delta \) sao cho tam giác OAM có diện tích bằng 4 (đvdt). Lời giải chi tiết I. PHẦN TRẮC NGHIỆM
Câu 1: Phương pháp: Biến đổi hàm số để sử dụng BĐT Cô-si làm mất x Cách giải: Ta có : \(f\left( x \right) = \frac{x}{2} + \frac{2}{{x - 1}}\)\( = \frac{{x - 1}}{2} + \frac{2}{{x - 1}} + \frac{1}{2}\) Có: \(x > 1 \Rightarrow x - 1 > 0\). Áp dụng bất đẳng thức Cô-si cho 2 số không âm \(\frac{{x - 1}}{2}\) và \(\frac{2}{{x - 1}}\) ta được: \(\begin{array}{l}\frac{{x - 1}}{2} + \frac{2}{{x - 1}}\\ \ge 2.\sqrt {\frac{{x - 1}}{2}.\frac{2}{{x - 1}}} = 2\\ \Rightarrow f\left( x \right) \ge 2 + \frac{1}{2} = \frac{5}{2}\end{array}\) Chọn C. Câu 2: Phương pháp: Giải hệ BPT, đếm số nghiệm nguyên. Cách giải: \(\left\{ \begin{array}{l}2x + 1 > 3x - 2\\ - x - 3 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x < 3\\x > - 3\end{array} \right.\) \( \Rightarrow - 3 < x < 3\) Lại có \(x \in \mathbb{Z} \Rightarrow x \in \left\{ { - 2;\,\, - 1;\,\,0;\,\,1;\,\,2} \right\}.\) Vậy có 5 nghiệm nguyên của hệ BPT Chọn C. Câu 3: Phương pháp: Cho đường thẳng \(\Delta :ax + by + c = 0\) và điểm \({M_0}\left( {{x_0};{y_0}} \right)\) \( \Rightarrow d\left( {{M_0};\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) Cách giải: \(d\left( {M;\Delta } \right) = \frac{{\left| {5.0 - 12.1 - 1} \right|}}{{\sqrt {{5^2} + {{12}^2}} }} = \frac{{13}}{{13}} = 1\) Chọn B. Câu 4: Phương pháp: Cos đối, sin bù, phụ chéo, khác pi tan. Cách giải: Ta có \(\Delta ABC\) \( \Rightarrow A + B + C = {180^o}\) \(\begin{array}{l} \Rightarrow \tan \left( {A + C} \right)\\ = - \tan \left( {{{180}^0} - A - C} \right)\\ = - \tan B\end{array}\) Vậy B đúng Chọn B. Câu 5: Phương pháp: Biến đổi hệ BPT và biện luận. Cách giải: Gọi G là trọng tâm tam giác ABC \( \Rightarrow G\left( { - 1;\frac{4}{3}} \right)\) \( \Rightarrow \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \left| {3\overrightarrow {MG} } \right| \)\(= 3MG\) Để \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) nhỏ nhất \( \Leftrightarrow MG\) nhỏ nhất \( \Leftrightarrow \) M là hình chiếu của G trên d Gọi \(d'\) là đường thẳng qua G vuông góc với d \( \Rightarrow d \cap d' = \left\{ M \right\}\) d nhận \(\overrightarrow n = \left( {2; - 1} \right)\) là VTPT \( \Rightarrow \overrightarrow {n'} = \left( {1;2} \right)\) là VTPT của \(d'\) \( \Rightarrow \) Phương trình \(d':\left( {x + 1} \right) + 2\left( {y - \frac{4}{3}} \right) = 0\) \( \Leftrightarrow x + 2y - \frac{5}{3} = 0\) Tọa độ điểm M là nghiệm của hệ : \(\left\{ \begin{array}{l}2x - y + 3 = 0\\x + 2y - \frac{5}{3} = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{{13}}{{15}} = a\\y = \frac{{19}}{{15}} = b\end{array} \right.\) \( \Rightarrow 5\left( {a + b} \right) = 5\left( { - \frac{{13}}{{15}} + \frac{{19}}{{15}}} \right) = 2\) Chọn C. Câu 6: Phương pháp: Sắp xếp các số liệu thống kê thành dãy không tăng hoặc không giảm. Số trung vị \({M_e}\) là số đứng giữa dãy nếu số phần tử là lẻ và là trung bình cộng của hai số đứng giữa nếu dãy số phần tử là chẵn. Cách giải: Có 7 phần tử là điểm cuả các em học sinh nên \({M_e} = {x_4} = 6.\) Chọn B. Câu 7: Phương pháp: \(\cos \left( {{\Delta _1};{\Delta _2}} \right) = \cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right) = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|\left| {\overrightarrow {{n_2}} } \right|}}\) trong đó \(\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} \) lần lượt là VTPT hoặc VTCP của \({\Delta _1};{\Delta _2}\) Cách giải: Ta có: \(\overrightarrow {{n_1}} = \left( {1;2} \right)\) là VTPT của \({\Delta _1}\) ; \(\overrightarrow {{n_2}} = \left( {2; - 4} \right)\) là VTPT của \({\Delta _2}\) \(\begin{array}{l} \Rightarrow \cos \left( {{\Delta _1};{\Delta _2}} \right)\\ = \cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right) = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|\left| {\overrightarrow {{n_2}} } \right|}}\\ = \frac{{\left| {1.2 - 2.4} \right|}}{{\sqrt {1 + 4} + \sqrt {4 + 16} }}\\ = \frac{6}{{\sqrt 5 .2\sqrt 5 }} = \frac{3}{5}\end{array}\) Chọn D. Câu 8: Phương pháp: Phương trình chính tắc của Elip có dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \({a^2} - {b^2} = {c^2}\) Trong đó: trục lớn \({A_1}{A_2} = 2a\); trục nhỏ \({B_1}{B_2} = 2b\); tiêu cự \({F_1}{F_2} = 2c\) ; tân sai \(e = \frac{c}{a}\) Cách giải: Elip \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\) có tâm sai: \(e = \frac{c}{a} = \frac{{\sqrt {{a^2} - {b^2}} }}{a}\) \( = \frac{{\sqrt {5 - 4} }}{{\sqrt 5 }} = \frac{1}{{\sqrt 5 }}\) Vậy B sai Chọn B. Câu 9: Phương pháp: Đường tròn \(\left( C \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = c\) có tâm \(I\left( {a;b} \right)\), bán kính \(R = \sqrt c \) Cách giải: Đường tròn tâm \(I(3; - 1)\) và bán kính \(R = 2\) có phương trình là: \({(x - 3)^2} + {(y + 1)^2} = 4\) Chọn C. Câu 10: Phương pháp: Đường tròn \(\left( C \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = c\) có tâm \(I\left( {a;b} \right)\), bán kính \(R = \sqrt c \) Cách giải: Đường tròn \(\left( C \right)\) có tâm nằm trên trục Oy\( \Rightarrow I\left( {0;\,\,b} \right)\) là tâm của đường tròn. \( \Rightarrow \left( C \right)\) có phương trình dạng: \({x^2} + {\left( {y - b} \right)^2} = c\) Vì \(A,B \in \left( C \right)\) ta có hệ: \(\left\{ \begin{array}{l}1 + {\left( {2 - b} \right)^2} = c\\9 + {\left( {1 - b} \right)^2} = c\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}1 + {\left( {2 - b} \right)^2} = c\\9 + {\left( {1 - b} \right)^2} = 1 + {\left( {2 - b} \right)^2}\end{array} \right.\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}1 + {\left( {2 - b} \right)^2} = c\\\left( {1 - b - 2 + b} \right)\left( {1 - b + 2 - b} \right) + 8 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}1 + {\left( {2 - b} \right)^2} = c\\ - 3 + 2b + 8 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}c = \frac{{85}}{4}\\b = - \frac{5}{2}\end{array} \right.\\ \Rightarrow R = \sqrt c = \frac{{\sqrt {85} }}{2}.\end{array}\) Chọn B. Câu 11: Phương pháp: Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( {O,R} \right)\) tại \(A \in \left( {O,R} \right) \Leftrightarrow OA \bot \Delta \) tại A Cách giải: Đường tròn \(\left( C \right)\) có tâm \(I\left( {2; - 3} \right) \Rightarrow \overrightarrow {IB} = \left( { - 3;4} \right)\) d là tiếp tuyến của \(\left( C \right)\) tại B \( \Rightarrow IB \bot d \Rightarrow \overrightarrow {IB} \) là 1 VTPT của d \( \Rightarrow \) Phương trình d: \( - 3\left( {x + 1} \right) + 4\left( {y - 1} \right) = 0\) \( \Leftrightarrow 3x - 4y + 7 = 0\) Chọn D. Câu 12: Phương pháp: Đường thẳng \(d\) đi qua \(A\left( {{x_0};\,\,{y_0}} \right)\) và có VTPT \(\overrightarrow n = \left( {a;\,\,b} \right)\) có phương trình tổng quát: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0.\) Cách giải: Ta có: \(\overrightarrow {AB} = \left( { - 9;3} \right) \Rightarrow \overrightarrow n = \left( {3;9} \right)\) là VTPT của đường thẳng AB \( \Rightarrow AB:3\left( {x - 3} \right) + 9\left( {y + 1} \right) = 0\) \( \Leftrightarrow 3x + 9y = 0\) \( \Leftrightarrow x + 3y = 0\) Chọn A. Câu 13: Phương pháp: Đường thẳng \(d\) đi qua \(A\left( {{x_0};\,\,{y_0}} \right)\) và có VTCP \(\overrightarrow u = \left( {a;\,\,b} \right)\) có phương trình tham số: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right..\) Cách giải: Ta có đường thẳng \(\frac{{x - 7}}{{ - 1}} = \frac{{y + 5}}{5}\) có VTCP là \(\overrightarrow u = \left( { - 1;5} \right)\) Đường thẳng cần tìm song song với đường thẳng trên nên nhận \(\overrightarrow u = \left( { - 1;5} \right)\) là VTCP. Phương trình tham số của đường thẳng qua \(M\left( {--2;3} \right)\) và song song với đường thẳng \(\frac{{x - 7}}{{ - 1}} = \frac{{y + 5}}{5}\) là: \(\left\{ \begin{array}{l}x = - 2 - t\\y = 3 + 5t\end{array} \right.\) Chọn A. Câu 14: Phương pháp: Rút gọn và thay tọa độ các điểm để kiểm chứng Cách giải: \(\begin{array}{l}5\left( {x + 2} \right) - 9 < 2x - 2y + 7\\ \Leftrightarrow 5x + 10 - 9 < 2x - 2y + 7\\ \Leftrightarrow 3x + 2y - 6 < 0\end{array}\) Ta có: \(3.2 + 2.3 - 6 = 6 > 0\) nên điểm \(\left( {2;3} \right)\) không thuộc miền nghiệm của BPT trên Chọn A. Câu 15: Phương pháp: Giải bất phương trình. Cách giải: Ta có: \(\begin{array}{l}\frac{{x - 1}}{{x - 3}} > 1\\ \Leftrightarrow \frac{{x - 1 - x + 3}}{{x - 3}} > 0\\ \Leftrightarrow \frac{2}{{x - 3}} > 0\\ \Leftrightarrow x - 3 > 0\\ \Leftrightarrow x > 3\end{array}\) Vậy tập nghiệm của BPT là \(\left( {3; + \infty } \right)\) Chọn C. Câu 16: Phương pháp: Thay giá trị của x vào BPT để kiểm chứng Cách giải: Ta có: \(1 - \sqrt {13 + 3.{{\left( { - \frac{7}{2}} \right)}^2}} \) \( \approx - 6,05 > 2.\left( { - \frac{7}{2}} \right) = - 7\) Vậy \(x = - \frac{7}{2}\) thỏa mãn bất phương trình \(1 - \sqrt {13 + 3{x^2}} > 2x\) Chọn D. Chú ý khi giải: HS có thể giải bất phương trình bằng cách đặt điều kiện sau đó bình phương hai vế. \(\begin{array}{l}1 - \sqrt {13 + 3{x^2}} > 2x\\ \Leftrightarrow 1 - 2x > \sqrt {13 + 3{x^2}} \\ \Leftrightarrow \left\{ \begin{array}{l}1 - 2x > 0\\1 - 4x + 4{x^2} > 13 + 3{x^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x < \frac{1}{2}\\{x^2} - 4x - 12 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x < \frac{1}{2}\\\left[ \begin{array}{l}x > 6\\x < - 2\end{array} \right.\end{array} \right. \Leftrightarrow x < - 2\\ \Rightarrow x = - \frac{7}{2}\,\,\left( {tm} \right)\end{array}\) Câu 17: Phương pháp: Thay giá trị a,b,c bất kỳ để kiểm chứng Cách giải: Thay \(a = 1;b = 2;c = 3\) vào BPT \(\frac{1}{{1 + {a^2}}} + \frac{1}{{1 + {b^2}}} + \frac{1}{{1 + {c^2}}}\)\( \ge \frac{1}{2}\left( {\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} \right)\) \( \Rightarrow \frac{4}{5} \ge \frac{{11}}{{12}}\) vô lý Vậy A sai. Chọn A. Câu 18: Phương pháp: \(\left| {f\left( x \right)} \right| \le g\left( x \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\ - g\left( x \right) \le f\left( x \right) \le g\left( x \right)\end{array} \right.\) Cách giải: \(\begin{array}{l}\left| {2x + 5} \right| \le {x^2} + 2x + 4\\ \Leftrightarrow \left\{ \begin{array}{l} - {x^2} - 2x - 4 \le 2x + 5\\2x + 5 \le {x^2} + 2x + 4\end{array} \right.\\\left( {{x^2} + 2x + 4 = {{\left( {x + 1} \right)}^2} + 3 > 0,\forall x} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 4x + 9 \ge 0\\{x^2} - 1 \ge 0\end{array} \right.\,\\\left( {do\,{x^2} + 4x + 9 = {{\left( {x + 2} \right)}^2} + 5 > 0,\forall x} \right)\\ \Leftrightarrow {x^2} - 1 \ge 0 \Leftrightarrow {x^2} \ge 1\\ \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x \le - 1\end{array} \right.\end{array}\) Chọn A. Câu 19: Phương pháp: Tìm giá trị đại diện của từng lớp và tính số trung bình Cách giải:
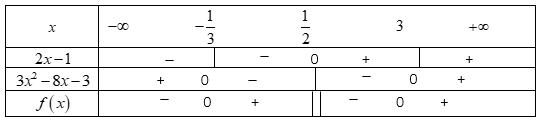
Chọn B. Câu 20: Phương pháp: Lập bảng xét dấu giải BPT. Cách giải: \(\begin{array}{l}\frac{{x - 1}}{{{x^2} + 4x + 3}} \le 0\\ \Leftrightarrow \frac{{x - 1}}{{\left( {x + 1} \right)\left( {x + 3} \right)}} \le 0\end{array}\) ĐKXĐ: \({x^2} + 4x + 3 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne - 1\\x \ne - 3\end{array} \right.\) Đặt \(f\left( x \right) = \frac{{x - 1}}{{{x^2} + 4x + 3}}\) . Ta có bảng:
Vậy \(f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \infty ; - 3} \right) \cup \left( { - 1;1} \right]\) Chọn B. Câu 21: Phương pháp: Chia cả tử và mẫu của P cho \(\cos x \ne 0\) Cách giải: Ta có \(\tan \alpha = 3 \Rightarrow \cos x \ne 0\) Chia cả tử và mẫu của P cho \(\cos x \ne 0\) ta được: \(\begin{array}{l}P = \frac{{3\sin \alpha + \cos \alpha }}{{\sin \alpha - \cos \alpha }}\\ = \frac{{\frac{{3\sin \alpha + \cos \alpha }}{{\cos \alpha }}}}{{\frac{{\sin \alpha - \cos \alpha }}{{\cos \alpha }}}}\\ = \frac{{3\tan \alpha + 1}}{{\tan \alpha - 1}}\\ = \frac{{3.3 + 1}}{{3 - 1}} = \frac{{10}}{2} = 5\end{array}\) Chọn D. Câu 22: Phương pháp: Giải bất phương trình \(f\left( x \right) < 0.\) Cách giải: \(\begin{array}{l}f(x) = {x^2} - 12x - 13 < 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 13} \right) < 0\\ \Leftrightarrow - 1 < x < 13\end{array}\) Chọn A. Câu 23: Phương pháp: Lưu ý cách biến đổi BPT. Cách giải: Ta có: \({x^2}\left( {x + 2} \right) > 0\) và \(\left( {x + 2} \right) > 0\) không tương đương vì \(x = 0\) ta có \(x + 2 > 0\) nhưng \({x^2}\left( {x + 2} \right) = 0\) Chọn D. Câu 24: Phương pháp: Phương trình đường thẳng d có hệ số góc là k có dạng \(y = kx + b\) Cách giải: Đường thẳng \(\left( d \right)\) có phương trình tổng quát: \(3x - 2y + 2019 = 0\)\( \Leftrightarrow y = \frac{3}{2}x + \frac{{2019}}{2}\) có hệ số góc \(k = \frac{3}{2}.\) Chọn D. II. TỰ LUẬN Bài 1. Phương pháp: Lập bảng xét dấu giải BPT Cách giải: Giải bất phương trình: \(\frac{{3{x^2} - 8x - 3}}{{2x - 1}} \ge 0\). ĐKXĐ : \(2x - 1 \ne 0 \Leftrightarrow x \ne \frac{1}{2}\) Đặt \(f\left( x \right) = \frac{{3{x^2} - 8x - 3}}{{2x - 1}} = \frac{{\left( {3x + 1} \right)\left( {x - 3} \right)}}{{2x - 1}}\) . Ta có bảng:
Vậy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \left[ { - \frac{1}{3};\frac{1}{2}} \right) \cup \left[ {3; + \infty } \right)\) Bài 2. Phương pháp: Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có biệt thức \(\Delta = {b^2} - 4ac\) - Nếu \(\Delta < 0\) thì với mọi \(x,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta = 0\)thì \(f\left( x \right)\) có nghiệm kép \(x = - \frac{b}{{2a}}\), với mọi \(x \ne - \frac{b}{{2a}},\,\,f\left( x \right)\) có cùng dấu với hệ số a. - Nếu \(\Delta > 0\),\(f\left( x \right)\)có 2 nghiệm \({x_1},{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) và luôn cùng dấu với hệ số a với mọi x ngoài khoảng \(\left( {{x_1};\,\,{x_2}} \right)\) và luôn trái dấu với hệ số a với mọi x trong khoảng \(\left( {{x_1};\,\,{x_2}} \right).\) Cách giải: Tìm m để bất phương trình \(3{x^2} + 2\left( {m - 1} \right)x + m + 5 > 0\) có tập nghiệm là \(\mathbb{R}\). Để bất phương trình \(3{x^2} + 2\left( {m - 1} \right)x + m + 5 > 0\) có tập nghiệm là \(\mathbb{R}\) \(\begin{array}{l} \Leftrightarrow \Delta ' = {\left( {m - 1} \right)^2} - 3.\left( {m + 5} \right) < 0\\ \Leftrightarrow {m^2} - 5m - 14 < 0\\ \Leftrightarrow - 2 < m < 7\end{array}\) Vậy với \( - 2 < m < 7\) thỏa mãn yêu cầu đề bài. Bài 3. Phương pháp: \(\begin{array}{l}1 + {\tan ^2}x = \frac{1}{{{{\cos }^2}x}}\\{\sin ^2}x + {\cos ^2}x = 1\\\sin 2x = 2\sin x\cos x\end{array}\) Cách giải: Cho \(\tan \alpha = - \sqrt 5 \,\,\,\,\left( {\frac{\pi }{2} < \alpha < \pi } \right)\). Tính \(\cos \alpha \) và \(\sin 2\alpha \). Do \(\frac{\pi }{2} < \alpha < \pi \Rightarrow \cos \alpha < 0\) Ta có: \(\frac{1}{{{{\cos }^2}\alpha }} = 1 + {\tan ^2}\alpha = 6\) \( \Rightarrow \cos \alpha = \frac{{ - \sqrt 6 }}{6}\) \(\begin{array}{l}\sin \alpha = \cos \alpha .\tan \alpha = \frac{{\sqrt {30} }}{6}\\ \Rightarrow \sin 2\alpha = 2\sin \alpha \cos \alpha = - \frac{{\sqrt 5 }}{3}\end{array}\) Bài 4. Phương pháp: a) Xác định VTPT và điểm đi qua. b) Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( C \right)\) tâm I bán kính R \( \Leftrightarrow d\left( {I;\Delta } \right) = R\) c) Gọi tọa độ điểm \(M\left( { - 3t - 5;t} \right) \in \Delta \). Tính OA. Từ giả thiết tính \(d\left( {M;OA} \right)\) theo m. Lập phương trình tìm m từ đó suy ra tọa độ điểm M. Cách giải: Trong hệ tọa độ Oxy, cho điểm\(A\left( {--1;2} \right)\) và đường thẳng \(\Delta :x + 3y + 5 = 0\). a) Viết phương trình đường thẳng d đi qua A và vuông góc với \(\Delta \). Vì \(d \bot \Delta \Rightarrow \overrightarrow {{n_d}} = \overrightarrow {{u_\Delta }} = \left( {3; - 1} \right)\) Phương trình đường thẳng \(d:3\left( {x + 1} \right) - \left( {y - 2} \right) = 0\) \( \Leftrightarrow 3x - y + 5 = 0\) b) Viết phương trình đường tròn \(\left( C \right)\) tâm \(A\left( {--1;2} \right)\) và tiếp xúc với \(\Delta \). Ta có: \(\left( C \right)\) tiếp xúc với \(\Delta \) nên \(R = d\left( {A;\Delta } \right) = \frac{{\left| { - 1 + 3.2 + 5} \right|}}{{\sqrt {{1^2} + {3^2}} }} = \sqrt {10} \) Vậy phương trình đường tròn \(\left( C \right)\): \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 10.\) c) Tìm điểm M trên đường thẳng \(\Delta \) sao cho tam giác OAM có diện tích bằng 4 (đvdt). Gọi tọa độ điểm \(M\left( { - 3t - 5;t} \right) \in \Delta \) Ta có: \(\overrightarrow {OA} = \left( { - 1;2} \right) \Rightarrow OA = \sqrt 5 ;\) \(\overrightarrow {{n_{OA}}} = \left( {2;1} \right)\) Phương trình đường thẳng OA: \(2x + y = 0\) Ta có: \({S_{OAM}} = \frac{1}{2}OA.d\left( {M;OA} \right) = 4\) \( \Leftrightarrow d\left( {M;OA} \right) = \frac{8}{{\sqrt 5 }}\) \(\begin{array}{l} \Leftrightarrow \frac{{\left| {2\left( { - 3t - 5} \right) + t} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \frac{8}{{\sqrt 5 }}\\ \Leftrightarrow \left| { - 5t - 10} \right| = 8\\ \Leftrightarrow \left[ \begin{array}{l} - 5t - 10 = 8\\ - 5t - 10 = - 8\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = - \frac{{18}}{5}\\t = - \frac{2}{5}\end{array} \right.\end{array}\) Vậy \(M\left( {\frac{{29}}{5}; - \frac{{18}}{5}} \right)\) hoặc \(M\left( { - \frac{{19}}{5}; - \frac{2}{5}} \right)\). Nguồn: Sưu tầm HocTot.XYZ
|