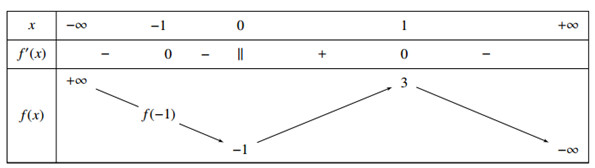
Đề số 83 - Đề thi thử THPT Quốc gia môn ToánĐáp án và lời giải chi tiết Đề số 83 - Đề thi thử THPT Quốc gia môn Toán đề trắc nghiệm Đề bài Câu 1. Cho hàm số \(y = f\left( x \right)\) liên tục trên R và có bảng biến thiên dưới đây
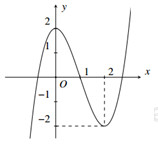
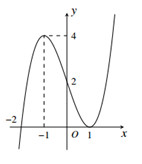
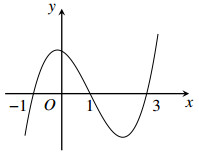
Có bao nhiêu giá trị nguyên của m để phương trình \(f\left( x \right) - 2 - m = 0\) có ba nghiệm phân biệt A. 5 B. 4 C. 3 D. 2 Câu 2. Đường cong ở hình bên là của đồ thị hàm số nào dưới đây ? A. \(y = {x^3} - 3{x^2} + 2\) B. \(y = {x^3} + 3{x^2} + 2\) C. \(y = - {x^3} + 3{x^2} + 2\) D. \(y = {x^3} - 3{x^2} + 1\) Câu 3. Trong không gian Oxyz cho các điểm \(A\left( {3;3;0} \right);\,\,B\left( {3;0;3} \right);\,\,C\left( {0;3;3} \right)\). Tìm tọa độ điểm I là tâm đường tròn ngoại tiếp tam giác ABC A. \(I\left( {2;3;2} \right)\) B. \(I\left( {2;2;0} \right)\) C. \(I\left( {2;2;2} \right)\) D. \(I\left( {0;2;2} \right)\) Câu 4 : Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên R. Đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ . Số điểm cực trị của hàm số \(g\left( x \right) = f\left( x \right) - 4x\) là : A.2 B.3 C.1 D.4 Câu 5 : \(\mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{\sqrt x - 1}}{{x + 1}}\) bằng A.0 B. \(\dfrac{1}{3}\) C. \( + \infty \) D. \( - \infty \) Câu 6. Hình tứ diện đều có bao nhiêu tâm đối xứng? A.1 B. 4 C.2 D.0 Câu 7. tìm phần thực , phần ảo của số phức sau : \(\) \(z = \dfrac{{3 - i}}{{1 + i}} + \dfrac{{2 + i}}{i}\) A. Phần thực là 2; phần ảo là -4 B. Phần thực là 2; phần ảo là 4i C. Phần thực là 2; phần ảo là 4 C. Phần thực là 2;phần ảo là -4i Câu 8: Cho hàm số \(y = f\left( x \right)\) liên tục trên R và có bảng biến thiên như hình vẽ :
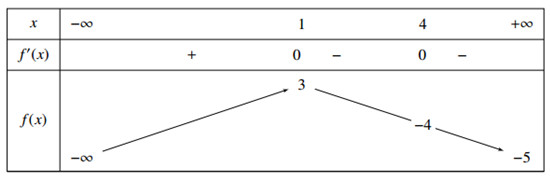
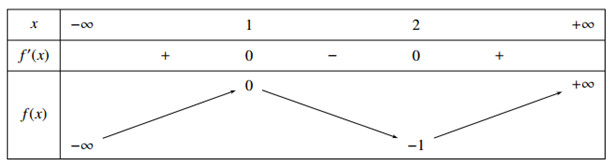
Phát biểu nào sau đây đúng ? A. \(f\left( x \right)\) có đúng 3 cực trị B. \(f\left( x \right)\) có đúng một cực tiểu C. \(f\left( x \right)\) có đúng một cực đại và không có cực tiểu D. \(f\left( x \right)\) có đúng hai điểm cực trị Câu 9. Trong không gian Oxyz , cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} + 2x + 4y + 2z - 5 = 0\). Tính bán kính r của mặt cầu trên A. \(\sqrt 3 \) B.1 C. \(\sqrt {11} \) D. \(3\sqrt 3 \) Câu 10. Một người vay vốn ngân hàng với số tiền 100 triệu đồng. Người đó dự định sau 5 năm thì trả hết nợ . Để trả hết nợ ngân hàng trong đúng 5 năm thì người đó phải đều đặn trả hàng tháng số tiền là a đồng. Biết lãi suất hàng tháng là 1,2%. Hỏi giá trị a gần nhất với số nào trong các số sau ? A. 2150600 đồng B. 2120600 đồng C. 2347600 đồng D. 2435600 đồng Câu 11. Cho các mệnh đề : (I) Số phức \(z = 2i\) là số thuần ảo (II) Nếu số phức z có phần thức là a , số phức z’ có phần thực là a’ thì z.z’ có phần thực là a.a’ (III) Tích của hai số phức z = a + bi và z’ = a’ + b’i \(\left( {a,b,a',b' \in R} \right)\) là số phức có phần ảo là \(ab' + a'b\) Số mệnh đề đúng trong 3 mệnh đề trên là A. 0 B. 3 C. 2 D. 1 Câu 12. Biết \(\int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{4\sin x - 2\cos x}}{{\sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right)\left( {\cos 2x + 1} \right)}}dx} = a + b\ln 2\), với a,b là các số nguyên. Tính \(S = ab\)? A. \(S = 10\) B. \(S = - 6\) C. \(S = 6\) D. \(S = 4\) Câu 13. Cho tam giác ABC vuông tại A, AH vuông góc với BC tại H , HB = 3,6 cm, HC = 6,4 cm. Quay miền tam giác ABC quanh đường thẳng AH ta thu được khối nón có thể tích bao nhiêu A. 205,89\(c{m^3}\) B. 65,54 \(c{m^3}\) C. 617,66\(c{m^3}\) D. 65,14\(c{m^3}\) Câu 14. Gọi S là tập hợp tất cả các số phức thỏa mãn \(\left\{ \begin{array}{l}|\overline z - 2 + 5i| = 2\\|z - 5 - i| = 3\end{array} \right.\). Hỏi tập S có bao nhiêu phần tử A. 0 B. 2 C. Vô số D. 1 Câu 15 : Nguyên hàm của hàm số \(f\left( x \right) = {3^x}\) là A. \(\int {f\left( x \right)dx = {3^x} + C} \) B. \(\int {f\left( x \right)dx} = {3^x}\ln 3 + C\)\(\) C. \(\int {f\left( x \right)dx} = \dfrac{{{3^{x + 1}}}}{{x + 1}} + C\) D. \(\int {f\left( x \right)dx} = \dfrac{{{3^x}}}{{\ln 3}} + C\) Câu 16. Tập nghiệm của bất phương trình \({\left( {\dfrac{1}{2}} \right)^{x - 2}} > {\left( {\dfrac{1}{2}} \right)^{2x - 5}}\) là A. \(\left( { - \infty ; - 3} \right)\) B. \(\left( {3; + \infty } \right)\) C. \(\left( { - 3; + \infty } \right)\) D. \(\left( { - \infty ;3} \right)\) Câu 17. Cho hàm số \(y = \dfrac{{{x^2} - 2x - 3}}{{{x^2} - 1}}\). Mệnh đề nào sau đây đúng A. Đồ thị hàm số có 1 tiệm cận đứng và 2 tiệm cận ngang B. Đồ thị hàm số có 2 tiệm cận đứng và 2 tiệm cận ngang C. Đồ thị hàm số có 2 tiệm cận đứng và 1 tiệm cận ngang D. Đồ thị hàm số có 1 tiệm cận đứng và 1 tiệm cận ngang Câu 18. Cho a > 0 , khác 1 ; x,y là các số thực dương. Mệnh đề nào sau đây đúng A.\({\log _a}\dfrac{x}{{{y^2}}} = \dfrac{{{{\log }_a}x}}{{2{{\log }_a}y}}\) B. \({\log _a}\dfrac{x}{{{y^2}}} = {\log _a}x - \dfrac{1}{2}{\log _a}y\) C. \({\log _a}\dfrac{x}{{{y^2}}} = \dfrac{1}{2}\left( {{{\log }_a}x - {{\log }_a}y} \right)\) D. \({\log _a}\dfrac{x}{{{y^2}}} = {\log _a}x - 2{\log _a}y\) Câu 19. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng 1, biết \(SO = \sqrt 2 \) và vuông góc với mặt đáy . Tính khoảng cách giữa hai đường thẳng SC và AB A. \(\dfrac{{\sqrt 5 }}{3}\) B. \(\dfrac{{\sqrt 2 }}{3}\) C. \(\sqrt 2 \) D .\(\dfrac{{2\sqrt 2 }}{3}\) Câu 20. Viết công thức tính thể tích V của phần vật thể nằm giữa hai mặt phẳng x = 0 và x = ln4, biết khi cắt vật thể bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x \(\left( {0 \le x \le \ln 4} \right)\) , ta được thiết diện là một hình vuông có độ dài cạnh là \(\sqrt {x.{e^x}} \) A. \(V = \int\limits_0^{\ln 4} {x{e^x}dx} \) B. \(V = \pi \int\limits_0^{\ln 4} {x{e^x}dx} \) C. \(V = \pi \int\limits_0^{\ln 4} {{{(x{e^x})}^2}dx} \) D. \(V = \int\limits_0^{\ln 4} {\sqrt {x{e^x}} dx} \) Câu 21. Trong không gian Oxyz , cho điểm \(A\left( {0;1;2} \right)\) và hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = 1 + t\\y = - 1 - 2t\\z = 2 + t\end{array} \right.;{d_2}:\dfrac{x}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z + 1}}{{ - 1}}\) . Viết phương trình mặt phẳng \(\left( \alpha \right)\) đi qua A và song song với hai đường thẳng \({d_1};{d_2}\) A. \(x + 3y - 5z - 13 = 0\) B. \(3x + y + z + 13 = 0\) C. \(x + 2y + z - 13 = 0\) D. \(x + 3y + 5z - 13 = 0\) \(\) \(\) Câu 22. Trong không gian Oxyz , cho đường thẳng \(d:\dfrac{{x - 2}}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z + 3}}{{ - 1}}\). Một vector chỉ phương của đường thẳng là A. \(\overrightarrow u = \left( {2;3;1} \right)\) B. \(\overrightarrow u = \left( { - 2; - 1;3} \right)\) C. \(\overrightarrow u = \left( {2;1; - 1} \right)\) D. \(\overrightarrow u = \left( { - 2;1; - 3} \right)\) Câu 23. Tính tích phân \(I = \int\limits_0^1 {{8^x}dx} \) A. \(I = 8\) B. \(I = \dfrac{8}{{3\ln 2}}\) C.\(I = \dfrac{7}{{3\ln 2}}\) D.\(I = 7\) Câu 24. Cho đa giác đều có 2n đỉnh , lấy ngẫu nhiên một đường chéo của đa giác này thì xác suất để đường chéo được chọn có độ dài lớn nhất bằng\(\dfrac{1}{9}\). Tìm n A. \(n = 4\) B. \(n = 6\) C. \(n = 10\) D. \(n = 5\) Câu 25. Trong không gian Oxyz , cho các điểm \(A\left( {2;1;0} \right);B\left( { - 2;3;2} \right)\) và đường thẳng \(d:\dfrac{{x - 1}}{2} = \dfrac{y}{1} = \dfrac{z}{{ - 2}}\). Gọi (S) là mặt cầu có tâm thuộc đường thẳng d và đi qua hai điểm A, B . Tìm tọa độ tâm I của mặt cầu (S) A. \(I\left( {1;1;2} \right)\) B.\(I\left( { - 1; - 1;2} \right)\) C.\(I\left( {2;1; - 1} \right)\) D.\(I\left( {0;2;1} \right)\) \(\) \(\) Câu 26. Tìm tập xác định của hàm số \(y = \dfrac{{\cot x}}{{1 - {{\sin }^2}x}} + \sin 3x\) A. \(R\backslash \left\{ {\dfrac{{k\pi }}{2};k \in Z} \right\}\) B.\(R\backslash \left\{ {k\pi ;k \in Z} \right\}\) C.\(R\backslash \left\{ {\dfrac{\pi }{2} + k2\pi ;k \in Z} \right\}\) D.\(R\backslash \left\{ {\dfrac{{ - \pi }}{2} + k2\pi ;k \in Z} \right\}\) \(\) \(\) Câu 27 . Hồng muốn qua nhà Hoa để cùng Hoa đến nhà Bình. Từ nhà Hồng đến nhà Hoa có 3 con đường đi , từ nhà Hoa tới nhà Bình có 2 con đường đi. Hỏi Hồng có bao nhiêu cách đi tới nhà Bình? A. 5 B. 6 C. 2 D. 4 Câu 28. Tính đạo hàm của hàm số \(y = {\sin ^2}x\) A. sin2x B. 2sinx C. – sin2x D. cos2x Câu 29. Trong không gian Oxyz , cho điểm\(A\left( { - 4; - 2;4} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = - 3 + 2t\\y = 1 - t\\z = - 1 + 4t\end{array} \right.\). Viết phương trình đường thẳng đi qua A và vuông góc với đường thẳng d A. \(\left\{ \begin{array}{l}x = - 4 + 3t\\y = - 2 + 2t\\z = 4 - t\end{array} \right.\) B.\(\left\{ \begin{array}{l}x = - 4 + 3t\\y = - 2 - t\\z = 4 - t\end{array} \right.\) C.\(\left\{ \begin{array}{l}x = - 4 - 3t\\y = - 2 + 2t\\z = 4 - t\end{array} \right.\) D.\(\left\{ \begin{array}{l}x = - 4 + t\\y = - 2 + t\\z = 4 + t\end{array} \right.\) \(\) Câu 30. Hình lăng trụ có 2018 đỉnh . Hỏi lăng trụ đó có bao nhiêu mặt bên ? A.2019 B.2018 C.1009 D.2020 Câu 31. Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ . Hàm số \(g\left( x \right) = f\left( {{x^2} - 1} \right)\) đồng biến trên khoảng nào dưới đây ? A. \(\left( {1; + \infty } \right)\) B.\(\left( {1;2} \right)\) C.\(\left( {0;1} \right)\) D.\(\left( { - 2; - 1} \right)\) Câu 32. Trong không gian Oxyz , cho mặt phẳng (P) : \(2x + 3y + z - 11 = 0\) và mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 4y - 2z - 8 = 8\) tiếp xúc với nhau tại điểm \(H\left( {{x_o};{y_o};{z_o}} \right)\). Tính tổng \(T = {x_o} + {y_o} + {z_0}\) A. \(T = 2\) B. \(T = 0\) C. \(T = 6\) D. \(T = 4\) Câu 33. Đồ thị hàm số \(y = \dfrac{{\ln \left( {x + 1} \right)}}{{{x^2}}}\) có bao nhiêu tiệm cận đứng ? A. 3 B. 1 C. 0 D. 2 Câu 34. Gọi d là tiếp tuyến của đồ thị \(\left( C \right):y = {x^3} + 3{x^2} + 1\) tại điểm \(A\left( {1;5} \right)\) và B là giao điểm thứ hai của tiếp tuyến với đồ thị hàm số. Khi đó diện tích tam giác OAB bằng A. \(S = 15\) B. \(S = 12\) C. \(S = 24\) D. \(S = 6\) Câu 35. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng \({60^o}\).Gọi M,N lần lượt là trung điểm các cạnh AB,BC. Tính cosin góc tạo bởi (SMN) và (ABC) A. \(\dfrac{1}{3}\) B.\(\dfrac{{\sqrt 3 }}{{12}}\) C.\(\dfrac{{12}}{{\sqrt {147} }}\) D.\(\dfrac{1}{7}\) Câu 36. Cho hai số thực a,b lớn hơn 1 thay đổi và thỏa mãn a + b = 10. Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình \(\left( {{{\log }_a}x} \right).\left( {{{\log }_b}x} \right) - 2{\log _a}x - 3{\log _b}x - 1 = 0\). Tìm giá trị lớn nhất của biểu thức \(S = {x_1}.{x_2}\) A. \(\dfrac{{4000}}{{27}}\) B.3456 C.\(\dfrac{{16875}}{{16}}\) D.15625 \(\) \(\) Câu 37. Một đa giác đều có 24 đỉnh , tất cả các cạnh của đa giác sơn màu xanh và tất cả các đường chéo của đa giác đó son màu đỏ. Gọi X là tập hợp tất cả các tam giác có 3 đỉnh là các đỉnh của đa giác đều trên. Người ta chọn ngẫu nhiên từ X một tam giác. Tính xác suất để chọn được tam giác có 3 cạnh cùng màu A. \(\dfrac{{27}}{{1290}}\) B.\(\dfrac{1}{{24}}\) C.\(\dfrac{{190}}{{253}}\) D.\(\dfrac{{24}}{{115}}\) Câu 38. Tìm hệ số chứa \({x^5}\) trong khai triển \({\left( {{x^3} + \dfrac{1}{x} + 2} \right)^6}\) A.356 B.210 C.735 D.480 Câu 39. Gọi S là tập hợp các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\dfrac{{{x^2} - mx + 2m}}{{x - 2}}} \right|\)trên [ -1 ; 1 ] bằng 3. Tính tổng tất cả các phần tử trong tập S A.5 B. \(\dfrac{{ - 8}}{3}\) C. - 1 D.\(\dfrac{5}{3}\)\(\) \(\) \(\) Câu 40. Trong không gian Oxyz , cho các điểm \(A\left( {1;0;0} \right);B\left( {0;2;0} \right);C\left( {0;0;4} \right)\). Viết phương trình đường thẳng đi qua trực tâm H của tam giác ABC và cuông góc với mặt phẳng (ABC) A.\(\dfrac{{x - 1}}{{ - 4}} = \dfrac{y}{2} = \dfrac{z}{1}\) B.\(\dfrac{{x - 1}}{4} = \dfrac{{y - 1}}{2} = \dfrac{z}{{ - 1}}\) C.\(\dfrac{x}{4} = \dfrac{y}{2} = \dfrac{z}{1}\) D.\(\dfrac{x}{4} = \dfrac{{y - 1}}{{ - 2}} = \dfrac{{z + 1}}{1}\) Câu 41. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của phần thực số phức \({\rm{w}} = {z^3} + \dfrac{1}{{{z^3}}}\). Trong đó z là số phức có |z| = 1 . Tính \(P = {M^2} + {m^2}\) A. \(P = 8\) B. \(P = 5\) C. \(P = 29\) D. \(P = 10\) Câu 42. Cho hàm số \(y = f\left( x \right)\) xác định trên R và có bảng biến thiên như sau :
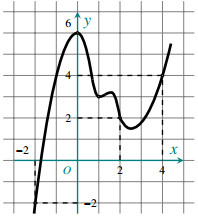
Tìm tất cả các giá trị của tham số m để đồ thị hàm số \(y = |f\left( {|x|} \right) + m|\) có 11 điểm cực trị A.\(m \ge 0\) B. \(m \le 0\) C. \(0 \le m \le 1\) D. 0 < m < 1 Câu 43. Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y = - 2{x^3} - mx + \dfrac{1}{{3{x^2}}}\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) A.3 B.6 C.4 D.5 Câu 44. Cho tứ diện ABCD thỏa mãn \(AB = CD = \sqrt {34} \) , \(BC = AD = \sqrt {41} \), \(AC = BD = 5\). Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD A.\(r = 5\sqrt 2 \) B.\(r = \dfrac{{5\sqrt 2 }}{2}\) C.\(r = \dfrac{1}{{\sqrt {10} }}\) D.\(r = \sqrt {10} \) Câu 45. Cho hình lăng trụ đứng ABCA’B’C’ có đáy là tam giác vuông can , AB = AC = a; AA’ = 2a. Tính khoảng cách giữa hai đường thẳng AB’ và BC’ A.\(\dfrac{{2a}}{{\sqrt {21} }}\) B.\(\dfrac{a}{{\sqrt 3 }}\) C.\(\dfrac{a}{{\sqrt {21} }}\) D.\(\dfrac{{2a}}{{\sqrt {17} }}\) Câu 46. Cho hình chóp S.ABC có AB = AC = 5a; BC = 6a và các mặt bên cùng tạo với đáy một góc \({60^o}\). Biết hình chiếu của S lên đáy là H và thuộc miền trong tam giác ABC. Tính thể tích V của khối chóp đã cho theo a A.\(V = 8{a^3}\) B.\(V = 6\sqrt 3 {a^3}\) C.\(V = \sqrt 3 {a^3}\) D.\(V = \dfrac{2}{{\sqrt 3 }}{a^3}\) Câu 47. Cho hàm số \(y = \dfrac{{x - 2}}{{x + 1}}\) có đồ thị (C) . Tiếp tuyến d của đồ thị (C) tạo với hai tiệm cận một tam giác có bán kính đường tròn nội tiếp lớn nhất. Khi đó khoảng cách từ I(-1;1) đến d bằng A.\(\sqrt 3 \) B.\(\sqrt 6 \) C.\(2\sqrt 3 \) D.\(2\sqrt 6 \) Câu 48. Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn\({u_1} = 3;{u_{n + 1}} = u_n^2 - 3{u_n} + 4,\forall n \in {N^*}\) . Biết dãy số \(\left( {{u_n}} \right)\) tăng và không bị chặn trên. Đặt \({v_n} = \dfrac{1}{{{u_1} - 1}} + \dfrac{1}{{{u_2} - 1}} + ... + \dfrac{1}{{{u_n} - 1}},n \in {N^*}\). Tính \(\mathop {\lim }\limits_{n \to + \infty } {v_n}\) A. \( - \infty \) B.\( + \infty \) C.1 D.0 Câu 49. Cho các số thực x,y,z không âm thỏa mãn \(0 < {\left( {x + y} \right)^2} + {\left( {y + z} \right)^2} + {\left( {z + x} \right)^2} \le 2\) . Biết giá trị lớn nhất của biểu thức \(P = {4^x} + {4^y} + {4^z} + \ln \left( {{x^4} + {y^4} + {z^4}} \right) \)\(\,- \dfrac{3}{4}{\left( {x + y + z} \right)^4}\) là \(\dfrac{a}{b}\) với a,b nguyên dương và \(\dfrac{a}{b}\) tối giản . Tính \(S = 2a + 3b\) A. \(S = 42\) B. \(S = 13\) C. \(S = 71\) D. \(S = 54\) Câu 50. Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên R. Đồ thị hàm số \(y = f\left( x \right)\)như hình vẽ. Khi đó giá trị của biểu thức \(\int\limits_0^4 {f'\left( {x - 2} \right)dx} + \int\limits_0^2 {f'\left( {x + 2} \right)dx} \) bằng bao nhiêu? A.6 B.2 C.-2 D.10 Lời giải chi tiết
Xem thêm: Lời giải chi tiết Đề thi thử THPT Quốc gia môn Toán tại HocTot.XYZ
HocTot.XYZ
|