Đề số 9 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 10Đáp án và lời giải chi tiết Đề số 9 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 10 Đề bài PHẦN 1 – TRẮC NGHIỆM (3 điểm, 15 câu hỏi, 30 phút) Câu 1: Trong mặt phẳng tọa độ \(Oxy,\)cho đường thẳng \(d:2x + 3y - 4 = 0.\) Vectơ nào sau đây là vectơ pháp tuyến của đường thẳng \(d?\) A.\(\overrightarrow {{n_1}} = \left( {3;2} \right)\) B.\(\overrightarrow {{n_2}} = \left( { - 4; - 6} \right)\) C. \(\overrightarrow {{n_3}} = \left( {2; - 3} \right)\) D. \(\overrightarrow {{n_4}} = \left( { - 2;3} \right)\) Câu 2: Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\,\,\,\left( {a \ne 0} \right).\) Điều kiện cần và đủ để \(f\left( x \right) < 0\,\,\forall \,x \in \mathbb{R}\) là: A.\(\left\{ \begin{array}{l}a > 0\\\Delta \ge 0\end{array} \right.\) B.\(\left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\) C.\(\left\{ \begin{array}{l}a < 0\\\Delta > 0\end{array} \right.\) D.\(\left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right.\) Câu 3: Tìm phương trình chính tắc của elip biết elip có độ dài trục lớn gấp đôi độ dài trục bé và có tiêu cự bằng \(4\sqrt 3 ?\) A. \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\) B. \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{24}} = 1\) C. \(\frac{{{x^2}}}{{24}} + \frac{{{y^2}}}{{16}} = 1\) D. \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\) Câu 4: Đường thẳng đi qua hai điểm \(A\left( {3;3} \right)\) và \(B\left( {5;5} \right)\) có phương trình tham số là: A. \(\left\{ \begin{array}{l}x = 3 + 2t\\y = 3 - 2t\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = 5 + t\\y = 5 - 2t\end{array} \right.\) C. \(\left\{ \begin{array}{l}x = 5 + 2t\\y = 2t\end{array} \right.\) D. \(\left\{ \begin{array}{l}x = t\\y = t\end{array} \right.\) Câu 5: Trên đường tròn định hướng có bán kính bằng \(4\) lấy một cung có số đo bằng \(\frac{\pi }{3}\) rad. Độ dài của cung tròn đó là: A. \(\frac{{4\pi }}{3}\) B. \(\frac{{3\pi }}{2}\) C. \(12\pi \) D. \(\frac{{2\pi }}{3}\) Câu 6: Tiêu cự của elip \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{4} = 1\) bằng: A. \(4\) B. \(2\) C. \(6\) D. \(1\) Câu 7: Tìm số nguyên lớn nhất của \(x\) để \(f\left( x \right) = \frac{{x + 4}}{{{x^2} - 9}} - \frac{2}{{x + 3}} - \frac{{4x}}{{3x - {x^2}}}\) nhận giá trị âm. A. \(x = - 2\) B. \(x = - 1\) C. \(x = 2\) D. \(x = 1\) Câu 8: Trong tam giác \(ABC,\) nếu có \({a^2} = b.c\) thì: A.\(\frac{1}{{h_a^2}} = \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}}\) B. \(\frac{1}{{h_a^2}} = \frac{2}{{{h_b}}} + \frac{2}{{{h_c}}}\) C. \(\frac{1}{{h_a^2}} = \frac{1}{{{h_b}}} - \frac{1}{{{h_c}}}\) D. \(h_a^2 = {h_b}.{h_c}\) Câu 9: Với giá trị nào của \(a\) thì hệ bất phương trình \(\left\{ \begin{array}{l}\left( { - {a^2} - 3} \right)x + a - 3 < 0\\\left( {{a^2} + 1} \right)x - a + 2 < 0\end{array} \right.\) có nghiệm? A. \(\left[ \begin{array}{l}a > 1\\a < - 3\end{array} \right.\) B. \( - 3 < a < 1\) C. \(\left[ \begin{array}{l}a > - 1\\a < - 3\end{array} \right.\) D. \( - 3 < a < - 1\) Câu 10: Đường tròn nào dưới đây đi qua điểm \(A\left( {4; - 2} \right)?\) A. \({x^2} + {y^2} - 6x - 2y + 9 = 0\) B. \({x^2} + {y^2} + 2x - 20 = 0\) C. \({x^2} + {y^2} - 2x + 6y = 0\) D. \({x^2} + {y^2} - 4x + 7y - 8 = 0\) Câu 11:(TH) Tập nghiệm của bất phương trình \( - {x^2} + 6x + 7 \ge 0\) là: A. \(\left[ { - 7;1} \right]\) B. \(\left[ { - 1;7} \right]\) C. \(\left( { - \infty ; - 7} \right] \cup \left[ {1; + \infty } \right)\) D. \(\left( { - \infty ; - 1} \right] \cup \left[ {7; + \infty } \right)\) Câu 12: Cho nhị thức bậc nhất \(f\left( x \right) = 23x - 20.\) Khẳng định nào sau đây đúng? A.\(f\left( x \right) > 0\) với \(\forall x \in \mathbb{R}\) B. \(f\left( x \right) > 0\) với \(\forall x \in \left( { - \infty ;\frac{{20}}{{23}}} \right)\) C. \(f\left( x \right) > 0\) với \(x > - \frac{5}{2}\) D. \(f\left( x \right) > 0\) với \(\forall x \in \left( {\frac{{20}}{{23}}; + \infty } \right)\) Câu 13: Biểu thức rút gọn của: \(A = {\cos ^2}a + {\cos ^2}\left( {a + b} \right) \)\(- 2\cos a.\cos b.\cos \left( {a + b} \right)\) bằng: A. \({\cos ^2}b\) B. \({\sin ^2}a\) C. \({\sin ^2}b\) D. \({\cos ^2}a\) Câu 14: Từ điểm \(A\left( {6;2} \right)\) ta kẻ hai tiếp tuyến với đường tròn \(\left( C \right):{x^2} + {y^2} = 4,\) tiếp xúc với \(\left( C \right)\) lần lượt tại \(P\) và \(Q.\) Tâm \(I\) của đường tròn ngoại tiếp tam giác \(APQ\) có tọa độ là: A. \(\left( {2;0} \right)\) B. \(\left( {1;1} \right)\) C. \(\left( {3;1} \right)\) D. \(\left( {4;1} \right)\) Câu 15: Tính \(B = \frac{{1 + 5\sin \alpha \cos \alpha }}{{3 - 2{{\cos }^2}\alpha }},\) biết \(\tan \alpha = 2.\) A. \(\frac{{15}}{{13}}\) B. \(\frac{{13}}{{14}}\) C. \(\frac{{ - 15}}{{13}}\) D. \(1\) PHẦN 2 – TỰ LUẬN (7 điểm, 3 bài, 60 phút) Bài 1: (2,0 điểm) Giải các bất phương trình sau: a) \(\frac{{2{x^2} + x - 1}}{{2 - x}} \ge 2\) b)\(x - \sqrt { - {x^2} - 4x + 21} \ge - 3\) Bài 2: (2,5 điểm) a) Cho \(\sin x = \frac{3}{5}\left( {\frac{\pi }{2} < x < \pi } \right).\) Tính \(\sin 2x,\,\,\cot x,\,\,\tan \left( {x - \frac{\pi }{4}} \right).\) b) Chứng minh rằng: \({\sin ^6}x + {\cos ^6}x = \frac{5}{8} + \frac{3}{8}\cos 4x.\) c) Cho tam giác \(ABC\) có các góc \(A,\,\,B,\,\,C\) thỏa mãn hệ thức: \(\sin A + \sin B + \sin C \)\(= \sin 2A + \sin 2B + \sin 2C\) Chứng minh tam giác \(ABC\) là tam giác đều. Bài 3: (2,5 điểm) Trong mặt phẳng với hệ tọa độ \(Oxy,\)cho hai điểm \(M\left( {1;3} \right),\,\,\,N\left( { - 1;2} \right)\) và đường thẳng \(d:3x - 4y - 6 = 0.\) a) Viết phương trình đường thẳng đi qua hai điểm \(M,\,N.\) b) Viết phương trình đường tròn tâm \(M\) và tiếp xúc với đường thẳng \(d.\) c) Cho đường tròn \(\left( C \right)\) có phương trình: \({x^2} + {y^2} - 6x - 4y - 3 = 0.\) Viết phương trình đường thẳng \(d'\) qua \(M\) cắt đường tròn \(\left( C \right)\) tại hai điểm \(A,\,B\) sao cho \(AB\) có độ dài nhỏ nhất. Lời giải chi tiết I. PHẦN TRẮC NGHIỆM
Câu 1 (NB) Phương pháp: Phương trình đường thẳng \(d:ax + by + c = 0\) có VTPT \(\overrightarrow n = k\left( {a;b} \right)\) Cách giải: Đường thẳng \(d:2x + 3y - 4 = 0\) có vectơ pháp tuyến \(\overrightarrow n = k\left( {2;3} \right)\) \( \Rightarrow \overrightarrow n = - 2\left( {2;3} \right) = \left( { - 4; - 6} \right)\) với \(k = - 2\) Chọn B. Câu 2 (NB) Phương pháp: Cho tam thức bậc hai:\(f\left( x \right) = a{x^2} + bx + c\,\,\,\left( {a \ne 0} \right).\) Khi đó \(f\left( x \right) < 0\,\,\forall x \in \mathbb{R}\) \( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right..\) Cách giải: Cho tam thức bậc hai:\(f\left( x \right) = a{x^2} + bx + c\,\,\,\left( {a \ne 0} \right).\) Khi đó \(f\left( x \right) > 0\,\,\forall x \in \mathbb{R}\) \( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right..\) Chọn D. Câu 3 (TH) Phương pháp: Sử dụng công thức \({b^2} = {a^2} - {c^2}\) với \(2c\) là tiêu cự, \(2a,\,2b\) là độ dài trục lớn và trục nhỏ của elip. Sau khi tìm \({a^2},{b^2}\), ta viết phương trình elip: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) Cách giải: Tiêu cự \(2c = 4\sqrt 3 \Rightarrow c = 2\sqrt 3 \) Độ dài trục lớn gấp đôi trục bé nên \(2a = 2\left( {2b} \right) \Rightarrow a = 2b\) Ta có: \({b^2} = {a^2} - {c^2}\)\( \Leftrightarrow {b^2} = {\left( {2b} \right)^2} - {\left( {2\sqrt 3 } \right)^2}\) \( \Leftrightarrow {b^2} = 4{b^2} - 12\) \(\begin{array}{l} \Leftrightarrow 3{b^2} = 12 \Leftrightarrow {b^2} = 4\\ \Rightarrow {a^2} = {\left( {2b} \right)^2} = 4{b^2} = 4.4 = 16\end{array}\) Khi đó ta có phương trình elip thỏa mãn bài toán là: \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\) Chọn A. Câu 4 (TH) Phương pháp: Đường thẳng \(d\) đi qua hai điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) và \(B\left( {{x_B};\,\,{y_B}} \right)\) nhận VTCP là \(\overrightarrow {AB} = \left( {a;\,\,b} \right)\) và có phương trình tham số là: \(\left\{ \begin{array}{l}x = {x_A} + at\\y = {y_A} + bt\end{array} \right..\) Cách giải: Ta có: \(\overrightarrow u = \overrightarrow {AB} = \left( {2;2} \right) = 2\left( {1;\,\,1} \right)\) \( \Rightarrow \) Phương trình tham số của đường thẳng \(AB\) là: \(\left\{ \begin{array}{l}x = 3 + t\\y = 3 + t\end{array} \right.\) Với \(t = - 3 \Rightarrow \left\{ \begin{array}{l}x = 0\\y = 0\end{array} \right. \Rightarrow AB\) đi qua điểm \(O\left( {0;\,0} \right).\) Khi đó ta có phương trình đường thẳng \(AB:\,\,\,\left\{ \begin{array}{l}x = t\\y = t\end{array} \right..\) Chọn D. Câu 5 (NB) Phương pháp: Sử dụng công thức \(l = R.\alpha \) với \(R\) là bán kính đường tròn, \(\alpha \,\,rad\) là số đo cung. Cách giải: Ta có: \(l = R.\alpha = 4.\frac{\pi }{3} = \frac{{4\pi }}{3}\) Chọn A. Câu 6 (TH) Phương pháp: Sử dụng phương trình elip: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \({b^2} = {a^2} - {c^2}\) trong đó \(2c\) là tiêu cự, \(2a,\,2b\) là độ dài trục lớn và trục nhỏ của elip. Tìm được \(c \Rightarrow 2c\) Cách giải: Ta có \({b^2} = {a^2} - {c^2}\) \(\begin{array}{l} \Leftrightarrow {c^2} = {a^2} - {b^2} = 5 - 4 = 1\\ \Rightarrow c = 1\end{array}\) \( \Rightarrow \) Tiêu cự của elop là: \(2c = 2.\) Chọn B. Câu 7 (VD) Phương pháp: Tìm điều kiện xác định và rút gọn biểu thức \(f\left( x \right).\) Lập bảng xét dấu tìm các khoảng cua \(x\) để \(f\left( x \right) < 0\) rồi tìm giá trị nguyên lớn nhất của \(x.\) Cách giải: Ta có: \(f\left( x \right) = \frac{{x + 4}}{{{x^2} - 9}} - \frac{2}{{x + 3}} - \frac{{4x}}{{3x - {x^2}}}\),\(\left( {x \ne 0,\,\,\,x \ne \pm 3} \right)\) \(\begin{array}{l}f\left( x \right) = \frac{{x + 4}}{{{x^2} - 9}} - \frac{2}{{x + 3}} - \frac{{4x}}{{3x - {x^2}}}\\ = \frac{{x + 4}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} - \frac{2}{{x + 3}} - \frac{{4x}}{{x\left( {3 - x} \right)}}\\ = \frac{{x\left( {x + 4} \right) - 2x\left( {x - 3} \right) + 4x\left( {x + 3} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \frac{{{x^2} + 4x - 2{x^2} + 6x + 4{x^2} + 12x}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}}\\ = \frac{{3{x^2} + 22x}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} = \frac{{3x + 22}}{{{x^2} - 9}}.\end{array}\) Ta có bảng xét dấu:
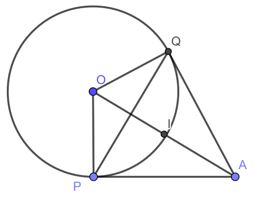
\( \Rightarrow f\left( x \right) = \frac{{x + 4}}{{{x^2} - 9}} - \frac{2}{{x + 3}} - \frac{{4x}}{{3x - {x^2}}}\) nhận giá trị âm khi \(x \in \left( { - \infty ;\frac{{ - 22}}{3}} \right) \cup \left( { - 3;0} \right) \cup \left( {0;3} \right)\) Vậy giá trị nguyên lớn nhất của \(x\) để \(f\left( x \right) = \frac{{x + 4}}{{{x^2} - 9}} - \frac{2}{{x + 3}} - \frac{{4x}}{{3x - {x^2}}}\) nhận giá trị âm là \(x = 2\) Câu 8 (VD) Phương pháp: Sử dụng công thức tính diện tích tam giác \(S = \frac{1}{2}a.{h_a}.\) Cách giải: Ta có: \(S = \frac{1}{2}a.{h_a} \Rightarrow {h_a} = \frac{{2S}}{a}\) \( \Rightarrow h_a^2 = \frac{{4{S^2}}}{{{a^2}}} = \frac{{4{S^2}}}{{b.c}}\)\( = \frac{{2S}}{b}.\frac{{2S}}{c} = {h_b}.{h_c}\) Chọn D. Câu 9 (VD) Phương pháp: Giải hệ bất phương trình bậc nhất một ẩn, lấy giao nghiệm của 2 bất phương trình. Tìm điều kiện để tập nghiệm đó khác rỗng. Cách giải: \(\left\{ \begin{array}{l}\left( { - {a^2} - 3} \right)x + a - 3 < 0\\\left( {{a^2} + 1} \right)x - a + 2 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left( { - {a^2} - 3} \right)x < 3 - a\\\left( {{a^2} + 1} \right)x < a - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x > \frac{{a - 3}}{{{a^2} + 3}}\\x < \frac{{a - 2}}{{{a^2} + 1}}\end{array} \right.\)\( \Leftrightarrow \frac{{a - 3}}{{{a^2} + 3}} < x < \frac{{a - 2}}{{{a^2} + 1}}\) Để hệ bất phương trình có nghiệm thì: \(\begin{array}{l}\frac{{a - 3}}{{{a^2} + 3}} < \frac{{a - 2}}{{{a^2} + 1}}\\ \Leftrightarrow \frac{{\left( {a - 3} \right)\left( {{a^2} + 1} \right) - \left( {a - 2} \right)\left( {{a^2} + 3} \right)}}{{\left( {{a^2} + 3} \right)\left( {{a^2} + 1} \right)}} < 0\\ \Leftrightarrow \left( {a - 3} \right)\left( {{a^2} + 1} \right) - \left( {a - 2} \right)\left( {{a^2} + 3} \right) < 0\\\left( {do\,\,\,\,\,\left( {{a^2} + 3} \right)\left( {{a^2} + 1} \right) > 0} \right)\\ \Leftrightarrow {a^3} - 3{a^2} + a - 3\\ - {a^3} + 2{a^2} - 3a + 6 < 0\,\,\,\\ \Leftrightarrow - {a^2} - 2a + 3 < 0\\ \Leftrightarrow \left[ \begin{array}{l}a > 1\\a < - 3\end{array} \right.\end{array}\) Chọn A. Câu 10 (NB) - Phương trình đường tròn Phương pháp: Thay lần lượt tọa độ điểm \(A\) vào từng phương trình đường tròn ở các đáp án rồi chọn đáp án đúng. Cách giải: Thay tọa độ điểm \(A\left( {4; - 2} \right)\) vào từng phương trình đường tròn ta có: Xét đáp án A: \({4^2} + {\left( { - 2} \right)^2} - 6.4 - 2.\left( { - 2} \right) + 9 = 0\)\( \Leftrightarrow 9 = 0\) (vô lý) Xét đáp án B: \({4^2} + {\left( { - 2} \right)^2} + 2.4 - 20 = 0 \Leftrightarrow 8 = 0\) (vô lý) Xét đáp án C: \({4^2} + {\left( { - 2} \right)^2} - 2.4 + 6.\left( { - 2} \right) = 0\)\( \Leftrightarrow 0 = 0\) (đúng) Xét đáp án D:\({4^2} + {\left( { - 2} \right)^2} - 4.4 + 7.\left( { - 2} \right) - 8 = 0\)\( \Leftrightarrow - 18 = 0\) (vô lý) Chọn C. Câu 11 (TH) Phương pháp: Sử dụng định lý về dấu tam thức bậc hai để giải bất phương trình \(a{x^2} + bx + c \ge 0\,\,\,\left( {a \ne 0} \right)\) Cách giải: \(\begin{array}{l} - {x^2} + 6x + 7 \ge 0\\ \Leftrightarrow {x^2} - 6x - 7 \le 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {x - 7} \right) \le 0\\ \Leftrightarrow - 1 \le x \le 7.\end{array}\) Vậy \( - {x^2} + 6x + 7 \ge 0\)\( \Leftrightarrow x \in \left[ { - 1;7} \right]\) Chọn B. Câu 12 (NB) Phương pháp: Giải bất phương trình bậc nhất 1 ẩn \(ax + b > 0.\) Cách giải: \(f\left( x \right) > 0 \Leftrightarrow 23x - 20 > 0 \Leftrightarrow x > \frac{{20}}{{23}}.\) Vậy \(f\left( x \right) > 0\) với \(\forall x \in \left( {\frac{{20}}{{23}}; + \infty } \right)\) Chọn D. Câu 13 (VD) Phương pháp: Sử dụng các công thức: \(\left\{ \begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}.\cos \frac{{a - b}}{2}\\\sin a.\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\\\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a - {\cos ^2}b\end{array} \right..\) Cách giải: \(\begin{array}{l}A = {\cos ^2}a + {\cos ^2}\left( {a + b} \right)\\ - 2\cos a.\cos b.\cos \left( {a + b} \right)\\ = {\cos ^2}a + {\cos ^2}\left( {a + b} \right)\\ - 2.\frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right].\cos \left( {a + b} \right)\\ = {\cos ^2}a + {\cos ^2}\left( {a + b} \right)\\ - {\cos ^2}\left( {a + b} \right) - \cos \left( {a - b} \right).\cos \left( {a + b} \right)\\ = {\cos ^2}a - \cos \left( {a - b} \right).\cos \left( {a + b} \right)\\ = \frac{{1 + \cos 2a}}{2} - \frac{1}{2}\left( {\cos 2a + \cos 2b} \right)\\ = \frac{1}{2} - \frac{{\cos 2b}}{2} = {\sin ^2}b.\end{array}\) Chọn C. Câu 14 (VD) Phương pháp: Chứng minh tứ giác \(OQPA\) là tứ giác nội tiếp đường tròn đường kính \(OA \Rightarrow I\) là trung điểm của \(OA.\) Cách giải:
Đường tròn \(\left( C \right):\,\,\,{x^2} + {y^2} = 4\) có tâm \(O\left( {0;0} \right)\) và bán kính \(R = 2.\) Ta có: \(A\left( {6;\,\,2} \right) \Rightarrow \overrightarrow {OA} = \left( {6;\,\,2} \right) \) \(\Rightarrow OA = 2\sqrt {10} > R \Rightarrow \) \(A\left( {6;2} \right)\) nằm ngoài đường tròn. Lại có: \(I\) là tâm đường tròn ngoại tiếp \(\Delta APQ\) với \(P,\,Q\) là hai tiếp điểm của hai tiếp tuyến kẻ từ \(A\) đến đường tròn \(\left( C \right).\) Khi đó ta chứng minh được tứ giác \(OPAQ\) là tứ giác nội tiếp. Lại có: \(\angle OQA = \angle OPA \Rightarrow \) Tâm \(I\) của đường tròn ngoại tiếp tứ giác \(OPAQ\) hay đường tròn ngoại tiếp \(\Delta APQ\) là trung điểm \(OA \Rightarrow \)\(I\left( {3;1} \right)\) Chọn C. Câu 15 (VD) Phương pháp: Chia cả tử và mẫu cho \({\cos ^2}\alpha \) rồi tính giá trị của biểu thức. Cách giải: \(\begin{array}{l}B = \frac{{1 + 5\sin \alpha \cos \alpha }}{{3 - 2{{\cos }^2}\alpha }}\\ = \frac{{\frac{1}{{{{\cos }^2}\alpha }} + 5.\frac{{\sin \alpha .\cos \alpha }}{{{{\cos }^2}\alpha }}}}{{3.\frac{1}{{{{\cos }^2}\alpha }} - 2.\frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}}}\\ = \frac{{1 + {{\tan }^2}\alpha + 5\tan \alpha }}{{3\left( {1 + {{\tan }^2}\alpha } \right) - 2}}\\ = \frac{{1 + {2^2} + 5.2}}{{3\left( {1 + {2^2}} \right) - 2}} = \frac{{15}}{{13}}.\end{array}\) Chọn A. II. TỰ LUẬN Bài 1 (VD) Phương pháp: a) Chuyển 2 sang vế trái để có bất phương trình thương bậc hai trên bậc nhất. Dựa vào định lý về dấu tam thức bậc hai, nhị thức bậc nhất để xét dấu vế trái. b) Chuyển bất phương trình về dạng \(\sqrt {f\left( x \right)} \le g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) \ge 0\\f\left( x \right) \le {g^2}\left( x \right)\end{array} \right.\) Cách giải: Giải các bất phương trình sau: a) \(\frac{{2{x^2} + x - 1}}{{2 - x}} \ge 2\,\,\,\,\left( * \right)\) ĐKXĐ: \(x \ne 2\) \(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow \frac{{2{x^2} + x - 1}}{{2 - x}} - 2 \ge 0\\ \Leftrightarrow \frac{{2{x^2} + x - 1 - 4 + 2x}}{{2 - x}} \ge 0\\ \Leftrightarrow \frac{{2{x^2} + 3x - 5}}{{2 - x}} \ge 0\end{array}\) Ta có bảng xét dấu: Vậy tập nghiệm \(S = \left( { - \infty ;\frac{{ - 5}}{2}} \right] \cup \left[ {1;2} \right)\) b)\(x - \sqrt { - {x^2} - 4x + 21} \ge - 3\) Bpt\( \Leftrightarrow \sqrt { - {x^2} - 4x + 21} \le x + 3\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x + 3 \ge 0\\ - {x^2} - 4x + 21 \ge {\rm{0}}\\ - {x^2} - 4x + 21 \le {\left( {x + 3} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\\left( {x + 7} \right)\left( {x - 3} \right) \le 0\\2{x^2} + 10x - 12 \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\ - 7 \le x \le 3\\\left[ \begin{array}{l}x \ge 1\\x \le - 6\end{array} \right.\end{array} \right. \Leftrightarrow 1 \le x \le 3\end{array}\) Vậy tập nghiệm \(S = \left[ {1;3} \right].\)
Bài 2 (VD) Phương pháp: a) Sử dụng công thức \({\sin ^2}x + {\cos ^2}x = 1\) và điều kiện \(\frac{\pi }{2} < x < \pi \) để tìm được \(\cos x\) Áp dụng các công thức \(\left\{ \begin{array}{l}\sin 2x = 2\sin x\cos x\\\cot x = \frac{{\cos x}}{{\sin x}}\\\,\tan x.\cot x = 1\\\,\,\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a.\tan b}}\,\,\end{array} \right.\) để tính giá trị các biểu thức. b) Áp dụng các công thức \({a^3} + {b^3} = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right)\) và \(\left\{ \begin{array}{l}{\sin ^2}x + {\cos ^2}x = 1\\2\sin x\cos x = \sin 2x\\{\sin ^2}x = \frac{{1 - \cos 2x}}{2}\end{array} \right.\) để biến đổi vế trái bằng vế phải. c) Áp dụng công thức \(\sin 2A + \sin 2B = 2\sin \left( {A + B} \right)\cos \left( {A - B} \right)\) để chứng minh \(VP \le VT\). Dấu bằng xảy ra \( \Leftrightarrow A = B = C\) Cách giải: a) Cho \(\sin x = \frac{3}{5}\left( {\frac{\pi }{2} < x < \pi } \right).\) Tính \(\sin 2x,\,\,\cot x,\,\,\tan \left( {x - \frac{\pi }{4}} \right).\) Ta có: \({\sin ^2}x + {\cos ^2}x = 1\) \(\begin{array}{l} \Leftrightarrow {\left( {\frac{3}{5}} \right)^2} + {\cos ^2}x = 1\\ \Rightarrow \cos x = \pm \frac{4}{5}\end{array}\) Kết hợp \(\frac{\pi }{2} < x < \pi \)\( \Rightarrow \cos x < 0 \Rightarrow \cos x = - \frac{4}{5}\) \(\begin{array}{l}\sin 2x = 2\sin x\cos x\\ = 2.\frac{3}{5}.\frac{{ - 4}}{5} = \frac{{ - 24}}{{25}}\\\cot x = \frac{{\cos x}}{{\sin x}} = \frac{{ - \frac{4}{5}}}{{\frac{3}{5}}} = \frac{{ - 4}}{3}\\ \Rightarrow \tan x = \frac{1}{{\cot x}} = \frac{{ - 3}}{4}\\\tan \left( {x - \frac{\pi }{4}} \right) = \frac{{\tan x - \tan \frac{\pi }{4}}}{{1 + \tan x.\tan \frac{\pi }{4}}}\\ = \frac{{\frac{{ - 3}}{4} - 1}}{{1 - \frac{3}{4}.1}} = - 7\end{array}\) b) Chứng minh rằng: \({\sin ^6}x + {\cos ^6}x = \frac{5}{8} + \frac{3}{8}\cos 4x.\)
Ta có: \(\begin{array}{l}VT = {\sin ^6}x + {\cos ^6}x\\ = {\left( {{{\sin }^2}x} \right)^3} + {\left( {{{\cos }^2}x} \right)^3}\\ = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^3}\\ - 3{\sin ^2}x.{\cos ^2}x\left( {{{\sin }^2}x + {{\cos }^2}x} \right)\\ = 1 - 3{\sin ^2}x.{\cos ^2}x\\ = 1 - \frac{3}{4}.{\left( {2\sin x\cos x} \right)^2}\\ = 1 - \frac{3}{4}{\sin ^2}2x\\ = 1 - \frac{3}{4}\left( {\frac{{1 - \cos 4x}}{2}} \right)\\ = \frac{5}{8} + \frac{3}{8}\cos 4x = VP\end{array}\) c) Cho tam giác \(ABC\) có các góc \(A,\,\,B,\,\,C\) thỏa mãn hệ thức: \(\sin A + \sin B + \sin C \)\(= \sin 2A + \sin 2B + \sin 2C\) Chứng minh tam giác \(ABC\) là tam giác đều. \(\begin{array}{l}\sin 2A + \sin 2B = 2\sin \left( {A + B} \right)\cos \left( {A - B} \right)\\ = 2\sin \left( {\pi - C} \right)\cos \left( {A - B} \right)\\ = 2\sin C.\cos \left( {A - B} \right)\end{array}\) Ta có: \(\left\{ \begin{array}{l}\sin C \ge 0\\\cos \left( {A - B} \right) \le 1\end{array} \right.\)\( \Rightarrow 2\sin C.\cos \left( {A - B} \right) \le 2\sin C\) Tương tự ta có: \(\left\{ \begin{array}{l}\sin 2B + \sin 2C \le 2\sin A\\\sin 2C + \sin 2A \le 2\sin B\end{array} \right.\) \( \Rightarrow \sin 2A + \sin 2B + \sin 2C\)\( \le \sin A + \sin B + \sin C\) Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}\cos \left( {A - B} \right) = 1\\\cos \left( {B - C} \right) = 1\\\cos \left( {C - A} \right) = 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}A - B = 0\\B - C = 0\\C - A = 0\end{array} \right.\) \( \Leftrightarrow A = B = C \Leftrightarrow \Delta ABC\)đều. Bài 3 (VDC) Phương pháp: a) Viết phương trình tham số của đường thẳng đi qua \(M\) có VTCP là \(\overrightarrow {NM} \) b) Viết phương trình đường tròn tâm \(M\) bán kính \(R = d\left( {M,d} \right)\) c) Chỉ ra \(M\) nằm trong đường tròn đã cho nên đường thẳng \(d'\) đi qua \(M\left( {1;3} \right)\) và cắt \(\left( C \right)\) tại hai điểm \(A,\,B\)sao cho \(AB\) nhỏ nhất \( \Leftrightarrow d' \bot MI\)(với \(I\) là tâm đường tròn \(\left( C \right)\)) Từ đó viết phương trình đường thẳng \(d'\) đi qua \(M\left( {1;3} \right)\) có VTPT \(\overrightarrow {MI} \) Cách giải: Trong mặt phẳng với hệ tọa độ \(Oxy,\)cho hai điểm \(M\left( {1;3} \right),\,N\left( { - 1;2} \right)\) và đường thẳng \(d:3x - 4y - 6 = 0.\) a) Viết phương trình đường thẳng đi qua hai điểm \(M,\,N.\) \(\overrightarrow {NM} = \left( {2;1} \right)\) Đường thẳng \(MN\) đi qua \(M\left( {1;3} \right)\) có VTCP \(\overrightarrow u = \left( {2;1} \right)\) có phương trình là \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + t\end{array} \right.\left( {t \in \mathbb{R}} \right)\) b) Viết phương trình đường tròn tâm \(M\) và tiếp xúc với đường thẳng \(d.\) Vì đường tròn tâm \(M\) bán kính \(R\) tiếp xúc với đường thẳng \(d\) nên \(d\left( {M,d} \right) = R\) \(R = d\left( {M,d} \right) = \frac{{\left| {3.1 - 4.3 - 6} \right|}}{{\sqrt {{3^2} + {{\left( { - 4} \right)}^2}} }} = 3\) Đường tròn tâm \(M\left( {1;3} \right)\) bán kính \(R = 3\) có phương trình là : \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 9\) c) Cho đường tròn \(\left( C \right)\) có phương trình: \({x^2} + {y^2} - 6x - 4y - 3 = 0.\) Viết phương trình đường thẳng \(d'\) qua \(M\) cắt đường tròn \(\left( C \right)\) tại hai điểm \(A,\,B\) sao cho \(AB\) có độ dài nhỏ nhất. Đường tròn \(\left( C \right)\) có tâm \(I\left( {3;2} \right);R = 4\) \(IM = \sqrt {{{\left( {1 - 3} \right)}^2} + {{\left( {3 - 2} \right)}^2}} = \sqrt 5 < R\) \( \Rightarrow M\) nằm trong đường tròn \(d'\) đi qua \(M\left( {1;3} \right)\) và cắt \(\left( C \right)\) tại hai điểm \(A,\,B\)sao cho \(AB\) nhỏ nhất \( \Leftrightarrow d' \bot MI\) \( \Rightarrow \overrightarrow {MI} = \left( {2; - 1} \right)\) là VTPT của \(d'\) Phương trình đường thẳng \(d'\) đi qua \(M\left( {1;3} \right)\) có VTPT \(\overrightarrow n = \left( {2; - 1} \right)\) là \(2\left( {x - 1} \right) - \left( {y - 3} \right) = 0\)\( \Leftrightarrow 2x - y + 1 = 0\). Nguồn: Sưu tầm HocTot.XYZ
|