Đề tham khảo thi vào 10 môn Toán Hà Nội năm 2025 - Đề số 2Tải về Câu 1: (1,5 điểm) 1) Đo chiều cao (đơn vị là cm) của học sinh lớp 9A cho kết quả như sau:
Lựa chọn câu để xem lời giải nhanh hơn
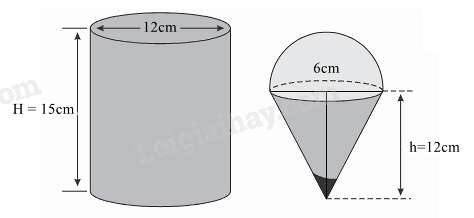
Đề bài Câu 1: (1,5 điểm) 1) Đo chiều cao (đơn vị là cm) của học sinh lớp 9A cho kết quả như sau: 156 157 164 166 166 165 157 156 155 158 160 163 163 161 162 159 159 160 160 160 159 158 160 160 158 163 162 162 162 161 162 161 163 161 163 161 164 166 165 165 Hãy lập bảng tần số ghép nhóm với các nhóm [155; 158), [158; 161), [161; 164), [164;167). Tính tần số tương đối của nhóm [161; 164) 2) Viết ngẫu nhiên một số tự nhiên lẻ có \(2\) chữ số. Xét biến cố A: “Số tự nhiên viết ra là bình phương của một số tự nhiên”. Tính xác suất của biến cố A. Câu 2: (1,5 điểm) Cho hai biểu thức: \(A = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(B = \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{4}{{\sqrt x - 3}} + \frac{{x - 4\sqrt x + 15}}{{9 - x}}\) với \(x > 0{\mkern 1mu} ;{\mkern 1mu} x \ne 9\) 1) Tính giá trị của biểu thức \(A\) khi \(x = 25\). 2) Chứng minh \(B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\). 3) Cho P = A: B. Tìm x nguyên để \(\left| P \right| + P = 0\). Câu 3: (2,5 điểm) 1) Bác Bình An vay ở một ngân hàng 500 triệu đồng để sản xuất trong thời hạn một năm. Lẽ ra đúng một năm sau bác phải trả cả tiền vốn lẫn tiền lãi, song bác đã được ngân hàng cho kéo dài thời hạn thêm 1 năm nữa, số tiền lãi của năm đầu được gộp vào với tiền vốn để tính lãi năm sau và lãi suất vẫn như cũ. Hết hai năm bác Bình An phải trả tất cả 605 triệu đồng. Hỏi lãi suất cho vay của ngân hàng đó là bao nhiêu phần trăm trong một năm? 2) Một người mua hai loại hàng và phải trả tổng cộng 2,17 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức \(10\% \) đối với loại hàng loại hàng thứ nhất và \(8\% \) đối với loại hàng thứ hai. Nếu thuế VAT là \(9\% \) đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng? 3) Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình: \(3{x^2} + 5x - 6 = 0\). Không giải phương trình, tính các giá trị của các biểu thức \({\rm{D = }}\frac{{{x_1}}}{{{x_2} + 2}} + \frac{{{x_2}}}{{{x_1} + 2}}\). Câu 4: (4 điểm) 1) Một hộp kem hình trụ có đường kính \(12{\mkern 1mu} {\rm{cm}}\) và chiều cao \(15{\mkern 1mu} {\rm{cm}}\) đựng đầy kem được đặt trên mặt bàn phẳng. a) Tính thể tích hộp kem. b) Hộp kem chứa kem sẽ được chia vào các bánh ốc quế hình nón có chiều cao \(12{\mkern 1mu} {\rm{cm}}\) và đường kính \(6{\mkern 1mu} {\rm{cm}}\), có hình bán cầu trên đỉnh như hình vẽ. Hãy tìm số que kem có thể chia được.
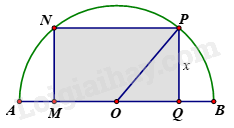
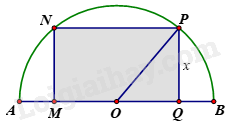
2) Cho đường tròn \(\left( {O{\mkern 1mu} ;{\mkern 1mu} R} \right)\), đường kính AB vuông góc với dây CD tại điểm \(I\) (\(I\) nằm giữa \(A\) và \(O\)). Lấy điểm \(E\) bất kì trên cung nhỏ BC \((\)E khác \(B\) và \(C\)). AE cắt CD tại \(K\). a) Chứng minh bốn điểm K, E, B, I cùng thuộc một đường tròn. b) Chứng minh \(AK.AE = AI.AB\). c) Gọi \(P\) là giao điểm của tia BE và tia DC, \(Q\) là giao điểm của AP và BK. Chứng minh IK là phân giác của \(\widehat {EIQ}\). Chứng minh OQ là tiếp tuyến của đường tròn ngoại tiếp tam giác PQE. Câu 5: (0,5 điểm) Tìm diện tích lớn nhất của hình chữ nhật \(MNPQ\) nội tiếp trong nửa đường tròn \(\left( O \right)\) bán kính \(10cm,\) biết một cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn (như hình vẽ).
-------- Hết -------- Lời giải chi tiết Câu 1: (1,5 điểm) 1) Đo chiều cao (đơn vị là cm) của học sinh lớp 9A cho kết quả như sau; 156 157 164 166 166 165 157 156 155 158 160 163 163 161 162 159 159 160 160 160 159 158 160 160 158 163 162 162 162 161 162 161 163 161 163 161 164 166 165 165 Hãy lập bảng tần số ghép nhóm với các nhóm [155; 158), [158; 161), [161; 164), [164;167). Tính tần số tương đối của nhóm [161; 164) 2) Viết ngẫu nhiên một số tự nhiên lẻ có \(2\) chữ số. Xét biến cố A: “Số tự nhiên viết ra là bình phương của một số tự nhiên”. Tính xác suất của biến cố A. Phương pháp 1) - Xác định tần số cho các nhóm để lập bảng tần số ghép nhóm. - Tần số tương đối của nhóm bằng: tần số của nhóm : tổng . 100%. 2) - Xác định không gian mẫu của phép thử, tính số phần tử của không gian mẫu. - Tính số kết quả thuận lợi của biến cố. - Xác suất của biến cố = số kết quả thuận lợi của biến cố : số phần tử của không gian mẫu. Lời giải 1) Bảng tần số ghép nhóm:
Vì tần số của nhóm [161; 164) là 15 nên tần số tương đối của nhóm [161; 164) là: \(\frac{{15}}{{40}}.100\% = 37,5\% \) 2) - Không gian mẫu của phép thử “Viết ngẫu nhiên một số tự nhiên lẻ có 2 chữ số” là: \(\Omega = \left\{ {11;{\mkern 1mu} {\mkern 1mu} 13;{\mkern 1mu} {\mkern 1mu} 15;{\mkern 1mu} {\mkern 1mu} ...;{\mkern 1mu} {\mkern 1mu} 97;{\mkern 1mu} {\mkern 1mu} 99} \right\}\) - Số phần tử của tập hợp \(\Omega \) là: \(\frac{{99 - 11}}{2} + 1 = 45\) (phần tử) - Các kết quả thuận lợi của biến cố \(A\): “Số tự nhiên viết ra là bình phương của \(1\) số tự nhiên” là: \(\left\{ {25;{\mkern 1mu} {\mkern 1mu} 49;{\mkern 1mu} {\mkern 1mu} 81} \right\}\). Biến cố này gồm \(3\) phần tử. - Xác suất của biến cố A là: \(3:45 = \frac{1}{{15}}\) Câu 2: (1,5 điểm) Cho hai biểu thức: \(A = \frac{{\sqrt x - 1}}{{\sqrt x }}\); \(B = \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{4}{{\sqrt x - 3}} + \frac{{x - 4\sqrt x + 15}}{{9 - x}}\) với \(x > 0{\mkern 1mu} ;{\mkern 1mu} x \ne 9\) 1) Tính giá trị của biểu thức \(A\) khi \(x = 25\). 2) Chứng minh \(B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\). 3) Cho P = A: B. Tìm x nguyên để \(\left| P \right| + P = 0\). Phương pháp 1) Kiểm tra điều kiện của x. Nếu thỏa mãn, thay \(x = 25\) vào biểu thức \(A\). 2) Kết hợp các tính chất của căn thức bậc hai để rút gọn biểu thức. 3) Rút gọn biểu thức P. Lập luận \(P \le 0\). Giải bất phương trình, kết hợp điều kiện ban đầu của \(x\) Lời giải 1) Thay \(x = 25\) (tmđk) vào A ta được \(A = \frac{{\sqrt {25} - 1}}{{\sqrt {25} }} = \frac{4}{5}\) Vậy với \(x = 25\) thì \(A = \frac{4}{5}\) 2) \(B = \frac{{2\sqrt x }}{{\sqrt x + 3}} + \frac{4}{{\sqrt x - 3}} - \frac{{x - 4\sqrt x + 15}}{{x - 9}}\) \( = \frac{{2\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} + \frac{{4\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}} - \frac{{x - 4\sqrt x + 15}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\) \( = \frac{{2x - 6\sqrt x + \left( {4\sqrt x + 12} \right) - \left( {x - 4\sqrt x + 15} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\) \( = \frac{{x + 2\sqrt x - 3}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\) \( = \frac{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right)}}\) \( = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\) Vậy \(B = \frac{{\sqrt x - 1}}{{\sqrt x - 3}}\). 3) \(P\)\( = A:B\)\( = \frac{{\sqrt x - 1}}{{\sqrt x }}:\frac{{\sqrt x - 1}}{{\sqrt x - 3}}\)\( = \frac{{\sqrt x - 1}}{{\sqrt x }}.\frac{{\sqrt x - 3}}{{\sqrt x - 1}}\)\( = \frac{{\sqrt x - 3}}{{\sqrt x }}\) (điều kiện bổ sung: \(x \ne 1\)) Vì \(\left| P \right| + P = 0\) nên \(\left| P \right| = - P\) Do đó \(P \le 0\), suy ra \(\frac{{\sqrt x - 3}}{{\sqrt x }} \le 0\) Vì \(x > 0\) nên \(\sqrt x > 0\), do đó \(\frac{{\sqrt x - 3}}{{\sqrt x }} \le 0\) khi \(\sqrt x - 3 \le 0\) suy ra \(\sqrt x \le 3\) nên \(x \le 9\) Kết hợp với điều kiện \(x > 0{\mkern 1mu} ;{\mkern 1mu} x \ne 9\), ta được \(0 < x < 9;x \ne 1\) Mà \(x \in \mathbb{Z}\) nên \(x \in \left\{ {2;3;4;5;6;7;8} \right\}\). Vậy \(x \in \left\{ {2;3;4;5;6;7;8} \right\}\). Câu 3: (2,5 điểm) 1) Bác Bình An vay ở một ngân hàng 500 triệu đồng để sản xuất trong thời hạn một năm. Lẽ ra đúng một năm sau bác phải trả cả tiền vốn lẫn tiền lãi, song bác đã được ngân hàng cho kéo dài thời hạn thêm 1 năm nữa, số tiền lãi của năm đầu được gộp vào với tiền vốn để tính lãi năm sau và lãi suất vẫn như cũ. Hết hai năm bác Bình An phải trả tất cả 605 triệu đồng. Hỏi lãi suất cho vay của ngân hàng đó là bao nhiêu phần trăm trong một năm? 2) Một người mua hai loại hàng và phải trả tổng cộng 2,17 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức \(10\% \) đối với loại hàng loại hàng thứ nhất và \(8\% \) đối với loại hàng thứ hai. Nếu thuế VAT là \(9\% \) đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng? 3) Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình: \(3{x^2} + 5x - 6 = 0\). Không giải phương trình, tính các giá trị của các biểu thức \({\rm{D = }}\frac{{{x_1}}}{{{x_2} + 2}} + \frac{{{x_2}}}{{{x_1} + 2}}\). Phương pháp 1) Gọi lãi suất của ngân hàng đó là \(x\) (\(x > 0\)) Biểu diễn số tiền phải trả sau năm thứ nhất, sau năm thứ 2 theo công thức: Số tiền phải trả = số tiền gốc + \(x\). số tiền gốc. Ta viết được phương trình biểu diễn số tiền phải trả sau hai năm. Giải phương trình để tìm \(x\), kiểm tra điều kiện và kết luận. 2) Gọi số tiền không kể thuế của loại hàng thứ nhất là \(x\) (triệu đồng), của loại hàng thứ hai là \(y\) (triệu đồng) (\(0 < x,y < 2,17\)). Viết hai phương trình biểu diễn số tiền phải trả khi: + thuế của loại hàng thứ nhất là 10% và thuế của loại hàng thứ hai là 8% + thuế của loại hàng thứ nhất và thuế của loại hàng thứ hai đều là 9% Lập được hệ phương trình, giải hệ để tìm \(x,y\). 3) Kiểm tra sự tồn tại của \({x_1},{x_2}\) theo \(a.c\). Áp dụng định lí Viète và biến đổi. Định lí Viète: \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}{x_2} = \frac{c}{a}\) Lời giải 1) Gọi lãi suất của ngân hàng đó là \(x\) (\(x > 0\)) Số tiền phải trả sau năm thứ nhất là: \(500 + 500x\) (triệu đồng). Số tiền phải trả sau năm thứ hai là: \(500 + 500x + \left( {500 + 500x} \right)x = 500{x^2} + 1000x + 500\) (triệu đồng). Vì sau hai năm bác Bình An phải trả 605 triệu đồng nên ta có phương trình: \(\begin{array}{l}500{x^2} + 1000x + 500 = 605\\500{x^2} + 1000x - 105 = 0\end{array}\) Giải phương trình ta được \({x_1} = 0,1\) (thỏa mãn); \({x_2} = - 2,1\) (loại). Vậy lãi suất mỗi năm của ngân hàng đó là \(0,1 = 10\% \). 2) Gọi số tiền không kể thuế của loại hàng thứ nhất là \(x\) (triệu đồng), của loại hàng thứ hai là \(y\) (triệu đồng) (\(0 < x,y < 2,17\)). Tổng số tiền phải trả là 2,17 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức \(10\% \) đối với loại hàng loạt hàng thứ nhất và \(8\% \) đối với loại hàng thứ hai nên ta có phương trình: \(\begin{array}{l}x + 10\% x + y + 8\% y = 2,17\\1,1x + 1,08y = 2,17\quad (1)\end{array}\) Nếu thuế VAT là \(9\% \) đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng nên ta có phương trình: \(\begin{array}{l}x + 9\% x + y + 9\% y = 2,18\\1,09x + 1,09y = 2,18\quad (2)\end{array}\) Vậy ta có hệ: \(\left\{ \begin{array}{l}1,1x + 1,08y = 2,17\\1,09x + 1,09y = 2,18\end{array} \right.\). Giải hệ phương trình ta được: \(\left\{ \begin{array}{l}x = 0,5\\y = 1,5\end{array} \right.\) (thỏa mãn). Vậy không kể thuế VAT thì loại hàng thứ nhất phải trả 0,5 triệu đồng, loại hàng thứ hai phải trả 1,5 triệu đồng. 3) Phương trình \(3{x^2} + 5x - 6 = 0\) có tích \(ac = 3{\rm{ }}{\rm{. }}\left( { - 6} \right) = - 18 < 0\) nên có nghiệm phân biệt \({x_1}\), \({x_2}\). Theo định lí Viète, ta có:\({x_1} + {x_2} = \frac{{ - 5}}{3}\) và \({x_1}{x_2} = \frac{{ - 6}}{3} = - 2\) (*). Ta có: \(D = \frac{{{x_1}}}{{{x_2} + 2}} + \frac{{{x_2}}}{{{x_1} + 2}}\) (điều kiện: \({x_1} \ne - 2,{x_2} \ne - 2\)) \(D = \frac{{{x_1}\left( {{x_1} + 2} \right) + {x_2}\left( {{x_2} + 2} \right)}}{{\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right)}}\) \(D = \frac{{\left( {x_1^2 + x_2^2} \right) + 2\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}\) \(D = \frac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right)}}{{{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) + 4}}\) Thay (*) vào \(D\), ta được: \(D = \frac{{{{\left( {\frac{{ - 5}}{3}} \right)}^2} - 2{\rm{ }}{\rm{. }}\left( { - 2} \right) + 2{\rm{ }} \cdot {\rm{ }}\left( {\frac{{ - 5}}{3}} \right)}}{{\left( { - 2} \right) + 2{\rm{ }} \cdot {\rm{ }}\left( {\frac{{ - 5}}{3}} \right) + 4}} = \frac{{ - 31}}{{12}}\) Câu 4: (4 điểm) 1) Một hộp kem hình trụ có đường kính \(12{\mkern 1mu} {\rm{cm}}\) và chiều cao \(15{\mkern 1mu} {\rm{cm}}\) đựng đầy kem được đặt trên mặt bàn phẳng. a) Tính thể tích hộp kem. b) Hộp kem chứa kem sẽ được chia vào các bánh ốc quế hình nón có chiều cao \(12{\mkern 1mu} {\rm{cm}}\) và đường kính \(6{\mkern 1mu} {\rm{cm}}\), có hình bán cầu trên đỉnh như hình vẽ. Hãy tìm số que kem có thể chia được.
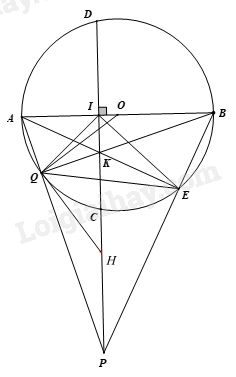
2) Cho đường tròn \(\left( {O{\mkern 1mu} ;{\mkern 1mu} R} \right)\), đường kính AB vuông góc với dây CD tại điểm \(I\) (\(I\) nằm giữa \(A\) và \(O\)). Lấy điểm \(E\) bất kì trên cung nhỏ BC\((\)E khác \(B\) và \(C\)). AE cắt CD tại \(K\). a) Chứng minh bốn điểm K, E, B, I cùng thuộc một đường tròn. b) Chứng minh \(AK.AE = AI.AB\). c) Gọi \(P\) là giao điểm của tia BE và tia DC, \(Q\) là giao điểm của AP và BK. Chứng minh IK là phân giác của \(\widehat {EIQ}\). Chứng minh OQ là tiếp tuyến của đường tròn ngoại tiếp tam giác PQE. Phương pháp 1) a) Tính thể tích kem trong hộp hình trụ: \({V_T} = \pi R_T^2.{h_T}\) b) Tính thể tích kem trong hộp = thể tích hình nón + thể tích hình bán cầu. + Thể tích hình nón: \({V_N} = \frac{1}{3}\pi R_N^2.{h_N}\) + Thể tích nửa hình cầu: \(\frac{1}{2}{V_C} = \frac{1}{2}.\frac{4}{3}\pi R_C^3\) Số que kem có thể chia được = thể tích kem trong hộp : thể tích kem trong một chiếc bánh ốc quế. 2) a) Chứng minh \(\widehat {KEB} = 90^\circ \) và \(\widehat {KIB} = 90^\circ \) nên \(\Delta KEB\) và \(\Delta KIB\) cùng thuộc đường tròn đường kính KB. Do đó K, E, B, I cùng thuộc một đường tròn. b) Chứng minh $\Delta AKI\backsim \Delta ABE$ suy ra tỉ số giữa hai cặp cạnh tương ứng của hai tam giác. c) * Chứng minh IK là phân giác của \(\widehat {EIQ}\). Chứng minh K là trực tâm của \(\Delta APB\) nên \(BQ \bot AP\left( {Q \in AP} \right)\) Tam giác AQK và tam giác AIK lần lượt vuông tại Q và I nên nội tiếp đường tròn đường kính AK suy ra AIKQ là tứ giác nội tiếp, nên \(\widehat {QAK} = \widehat {QIK}\). Kết hợp với \(\widehat {KIE} = \widehat {KBE}\) và \(\widehat {QAK} = \widehat {KBE}\) suy ra \(\widehat {KIE} = \widehat {KIQ}\) hay IK là phân giác của \(\widehat {EIQ}\) * Chứng minh OQ là tiếp tuyến của đường tròn ngoại tiếp tam giác PQE. Gọi H là trung điểm của PK, khi đó đường tròn (H; HP) ngoại tiếp tam giác PQE. Ta cần chứng minh \(\widehat {OQH} = 90^\circ \) hay \(OQ \bot QH\): + Chứng minh \(\Delta OQB\) là tam giác cân tại \(O\) nên \(\widehat {OQK} = \widehat {OBQ}\) + Chứng minh $\Delta IBK\backsim \Delta QPK$ (g-g) suy ra \(\widehat {OBQ} = \widehat {QPK}\) + Chứng minh \(\widehat {HQP} = \widehat {QPK}\) (tam giác HPQ cân tại H). Ta được \(\widehat {OQK} = \widehat {{\kern 1pt} HQP}\). Sử dụng cộng góc để được \(\widehat {OQH} = \widehat {KQP} = 90^\circ \) nên \(OQ \bot QH\). Lời giải 1) a) Thể tích kem trong hộp hình trụ là: \({V_T} = \pi R_T^2.{h_T}\)\( = \pi {\left( {\frac{{12}}{2}} \right)^2}.15\)\( = 540\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\) b) Thể tích kem trong bánh ốc quế hình nón có hình bán cầu trên đỉnh là \({V_{kem}} = \frac{1}{3}\pi R_N^2.{h_N} + \frac{1}{2}.\frac{4}{3}\pi R_C^3\)\( = \frac{1}{3}\pi {\left( {\frac{6}{2}} \right)^2}.12 + \frac{1}{2}.\frac{4}{3}.\pi .{\left( {\frac{6}{2}} \right)^3}\)\( = 54\pi {\mkern 1mu} {\mkern 1mu} (c{m^3})\) Vậy số que kem có thể chia được là: \(\frac{{540\pi }}{{54\pi }} = 10\) que. 2)
a) Xét \(\left( {O{\mkern 1mu} ;{\mkern 1mu} R} \right)\) có: \(\widehat {AEB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) hay \(\widehat {KEB} = 90^\circ \) Đường kính AB vuông góc với dây CD tại điểm \(I\) nên \(\widehat {KIB} = 90^\circ \) Xét \(\Delta KEB\) vuông tại E có cạnh huyền KB suy ra K, E, B thuộc đường tròn đường kính KB (1) Xét \(\Delta KIB\) vuông tại I có cạnh huyền KB suy ra K, I, B thuộc đường tròn đường kính KB (2) Do đó K, E, B, I cùng thuộc một đường tròn. b) Xét \(\Delta AKI\) và \(\Delta ABE\), ta có: $\widehat{A}$ là góc chung \(\widehat {AIK} = \widehat {AEB} = 90^\circ \) suy ra $\Delta AKI\backsim \Delta ABE$ \(\left( {g - g} \right)\) Do đó \(\frac{{AK}}{{AB}} = \frac{{AI}}{{AE}}\) nên \(AK.AE = AI.AB\) (đpcm) c) * Chứng minh IK là phân giác của \(\widehat {EIQ}\). Xét \(\Delta APB\) có: \(PI \bot AB\left( {I \in AB} \right)\); \(AE \bot PB\left( {E \in PB} \right)\); \(PI\) cắt \(AE\) tại \(K\) nên \(K\) là trực tâm của \(\Delta APB\) Suy ra \(BQ \bot AP\left( {Q \in AP} \right)\) nên \(\widehat {AQB} = 90^\circ \) hay \(\widehat {AQK} = 90^\circ \) Đường kính AB vuông góc với dây CD tại điểm \(I\) nên \(\widehat {AIK} = 90^\circ \) Tam giác AQK và tam giác AIK lần lượt vuông tại Q và I nên nội tiếp đường tròn đường kính AK, do đó bốn điểm A, I, Q, K cùng thuộc đường tròn đường kính AK suy ra AIKQ là tứ giác nội tiếp suy ra \(\widehat {QAK} = \widehat {QIK}\) (hai góc nội tiếp cùng chắn ) Ta có: KEBI là tứ giác nội tiếp (cmt) nên \(\widehat {KIE} = \widehat {KBE}\) (hai góc nội tiếp cùng chắn $\overset\frown{EK}$) Ta có: \(\widehat {AQB} = 90^\circ \) nên \(\Delta AQB\) nội tiếp \(\left( {O;R} \right)\), do đó \(Q \in \left( {O;R} \right)\) Lại có: \(\widehat {QAK} = \widehat {KBE}\) (hai góc nội tiếp cùng chắn $\overset\frown{QE}$) suy ra \(\widehat {KIE} = \widehat {KIQ}\) hay IK là phân giác của \(\widehat {EIQ}\) (đpcm) * Chứng minh OQ là tiếp tuyến của đường tròn ngoại tiếp tam giác PQE. Xét \(\Delta OQB\), ta có: \(OQ = OB = R\) Suy ra \(\Delta OQB\) là tam giác cân tại \(O\) Do đó \(\widehat {OQB} = \widehat {OBQ}\) hay \(\widehat {OQK} = \widehat {OBQ}\) \(\left( 1 \right)\) Xét \(\Delta IBK\) và \(\Delta QPK\), ta có: \(\widehat {IKB} = \widehat {QKP}\) (hai góc đối đỉnh) \(\widehat {KQP} = \widehat {KIB} = 90^\circ \) Suy ra $\Delta IBK\backsim \Delta QPK$ (g-g) Do đó \(\widehat {IBK} = \widehat {QPK}\) (hai góc tương ứng) hay \(\widehat {OBQ} = \widehat {QPK}\) \(\left( 2 \right)\) Xét tam giác KQP và tam giác KEP lần lượt vuông tại Q và E nên nội tiếp đường tròn đường kính PK, suy ra P, Q, K, E thuộc đường tròn đường kính PK và đường tròn (H; HP) ngoại tiếp tam giác PQE. Gọi H là trung điểm của PK, khi đó HP = HQ nên tam giác HPQ cân tại H, do đó \(\widehat {PQH} = \widehat {QPK}\) hay \(\widehat {HQP} = \widehat {QPK}\) (3) Từ (1), (2) và (3) suy ra: \(\widehat {OQK} = \widehat {{\kern 1pt} HQP}\) Mà \(\widehat {HQO} = \widehat {OQK} + \widehat {KQH} = \widehat {HQP} + \widehat {KQH} = \widehat {HQP} = 90^\circ \) Suy ra \(\widehat {OQH} = 90^\circ \) hay \(OQ \bot QH\) Do đó OQ là tiếp tuyến của đường tròn ngoại tiếp tam giác PQE (đpcm). Câu 5: (0,5 điểm) Tìm diện tích lớn nhất của hình chữ nhật \(MNPQ\) nội tiếp trong nửa đường tròn \(\left( O \right)\) bán kính \(10cm,\) biết một cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn (như hình vẽ).
Phương pháp Gọi \(x\left( {cm} \right)\) là độ dài cạnh hình chữ nhật không nằm dọc theo đường kính đường tròn \(\left( {0 < x < 10} \right)\) Khi đó áp dụng định lí Pythagore để tính OQ theo \(x\), ta tính được \(MQ = 2.OQ\). Tính diện tích hình chữ nhật MNPQ theo \(x\). Áp dụng bất đẳng thức Cauchy cho 2 số: \(2\sqrt {ab} \le a + b\). Dấu bằng xảy ra khi \(a = b \ge 0\) Dấu “=” xảy ra khi là diện tích lớn nhất của hình chữ nhật. Lời giải Gọi \(x\left( {cm} \right)\) là độ dài cạnh hình chữ nhật không nằm dọc theo đường kính đường tròn \(\left( {0 < x < 10} \right)\) Áp dụng định lí Pythagore trong tam giác OPQ, ta có: \(OQ = \sqrt {O{P^2} - P{Q^2}} = \sqrt {{{10}^2} - {x^2}} \) Khi đó độ dài cạnh MQ của hình chữ nhật nằm dọc trên đường kính của đường tròn là: \(MQ = 2.OQ = 2\sqrt {{{10}^2} - {x^2}} \left( {cm} \right)\) Diện tích hình chữ nhật MNPQ là: \(S = x.2\sqrt {100 - {x^2}} = 2\sqrt {{x^2}.\left( {100 - {x^2}} \right)} \left( {c{m^2}} \right)\) Áp dụng bất đẳng thức Cauchy cho hai số, ta có: \(2\sqrt {{x^2}.\left( {100 - {x^2}} \right)} \le {x^2} + 100 - {x^2} = 100\). Dấu “=” xảy ra khi \({x^2} = 100 - {x^2}\) Suy ra \(2{x^2} = 100\) \({x^2} = 50\) \(x = 5\sqrt 2 \) (vì \(x > 0\)) Vậy diện tích lớn nhất của hình chữ nhật là \(100c{m^2}\) khi \(x = 5\sqrt 2 \left( {cm} \right)\). Tần số tương đối của nhóm [161; 164) là: \(\frac{{15}}{{40}}.100\% = 37,5\% \)
|