Đề thi vào 10 môn Toán Bạc Liêu năm 2025Tải vềCâu 1 (0,5 điểm). Giải phương trình: \(\left( {2x - 3} \right)\left( {x + 5} \right) = 0\).
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài Câu 1 (0,5 điểm). Giải phương trình: \(\left( {2x - 3} \right)\left( {x + 5} \right) = 0\). Câu 2 (1,5 điểm). a) Tính giá trị của biểu thức: \(A = \sqrt {49} - \sqrt {25} \). b) Cho biểu thức \(B = \frac{{\sqrt x }}{{\sqrt x - 6}} - \frac{6}{{\sqrt x + 6}}\) (với \(x \ge 0;x \ne 36\)). Rút gọn biểu thức B và tính giá trị của biểu thức B khi \(x = 6\). Câu 3 (1,5 điểm). Cho hàm số \(y = \frac{2}{3}{x^2}\). a) Tìm hệ số a của \({x^2}\). b) Vẽ đồ thị của hàm số đã cho. Câu 4 (1,5 điểm). Cho phương trình bậc hai \(2{x^2} + 3x - 2 = 0\) a) Xác định các hệ số \(a,b,c\) của phương trình. b) Giải phương trình đã cho. Câu 5 (1,0 điểm). Gieo đồng thời hai con xúc xắc cân đối và đồng chất. Tính xác suất của biến cố A: “Tổng số chấm xuất hiện trên hai mặt con xúc xắc bằng 5”.
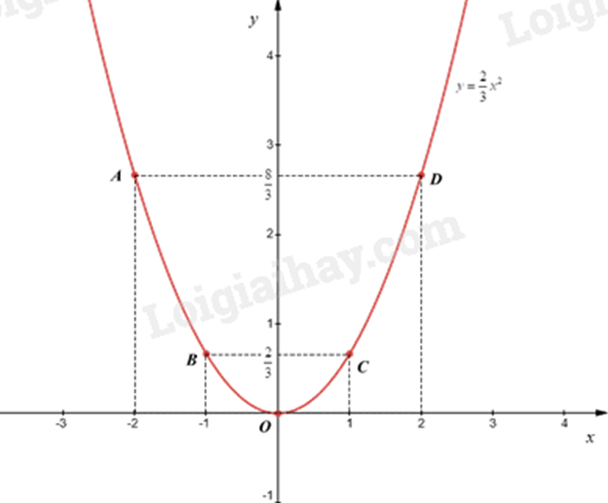
Câu 6 (1,0 điểm). Để chuẩn bị khen thưởng cho học sinh cuối năm học, Trường THCS X cần mua 1400 quyển vở và 700 cây bút ở Nhà sách Y để làm phần thưởng. Nhà trường dự tính mua với giá niêm yết sẽ cần 22 triệu 400 nghìn đồng, nhưng do mua với số lượng lớn nên Nhà sách Y đã giảm giá \(5{\rm{\% }}\) cho mỗi quyển vở và \(10{\rm{\% }}\) cho mỗi cây bút, vì thế nhà trường chỉ cần trả 21 triệu đồng. Tính giá tiền niêm yết của mỗi quyển vở và mỗi cây bút. Câu 7 (0,5 điểm). Một tam giác vuông có cạnh huyền dài 13cm và diện tích bằng \(30{m^2}\). Lập phương trình bậc hai một ẩn có hai nghiệm là độ dài hai cạnh góc vuông của tam giác đã cho. Câu 8 (2,5 điểm). Cho đường tròn (O; R) có đường kính AB vuông góc với dây cung CD tại điểm I (I nằm giữa A và O). Lấy điểm E bất kỳ trên cung nhỏ BC (E khác B và C). Hai đoạn thẳng AE và CD cắt nhau tại K. a) Chứng minh tứ giác KEBI là tứ giác nội tiếp. b) Chứng minh: \(AK \cdot AE = AB \cdot AI\). c) Gọi P là giao điểm cùa tia BE và tia DC, Q là giao điểm của hai đường thẳng AP và BK. Chứng minh OQ là tiếp tuyến của đường tròn ngoại tiếp \(\Delta PQE\). -------- Hết -------- Lời giải chi tiết Câu 1 (0,5 điểm). Giải phương trình: \(\left( {2x - 3} \right)\left( {x + 5} \right) = 0\). Lời giải: \(\left( {2x - 3} \right)\left( {x + 5} \right) = 0\) Phương trình tích có hai nghiệm thoả mãn: +) \(2x - 3 = 0\) suy ra \(x = \frac{3}{2}\) +) \(x + 5 = 0\) suy ra \(x = - 5\) Vậy phương trình có hai nghiệm \(x = \frac{3}{2}\) và \(x = - 5\) Câu 2 (1,5 điểm). a) Tính giá trị của biểu thức: \(A = \sqrt {49} - \sqrt {25} \). b) Cho biểu thức \(B = \frac{{\sqrt x }}{{\sqrt x - 6}} - \frac{6}{{\sqrt x + 6}}\) (với \(x \ge 0;x \ne 36\)). Rút gọn biểu thức B và tính giá trị của biểu thức B khi \(x = 6\). Lời giải: a) Ta có: \(A = \sqrt {49} - \sqrt {25} = 7 - 5 = 2\). b) +) ĐKXĐ: \(x \ge 0;x \ne 36\) \(\begin{array}{l}B = \frac{{\sqrt x }}{{\sqrt x - 6}} - \frac{6}{{\sqrt x + 6}}\\ = \frac{{\sqrt x \left( {\sqrt x + 6} \right)}}{{\left( {\sqrt x - 6} \right)\left( {\sqrt x + 6} \right)}} - \frac{{6\left( {\sqrt x - 6} \right)}}{{\left( {\sqrt x - 6} \right)\left( {\sqrt x + 6} \right)}}\\ = \frac{{x + 6\sqrt x - \left( {6\sqrt x - 36} \right)}}{{\left( {\sqrt x - 6} \right)\left( {\sqrt x + 6} \right)}}\\ = \frac{{x + 6\sqrt x - 6\sqrt x + 36}}{{\left( {\sqrt x - 6} \right)\left( {\sqrt x + 6} \right)}}\\ = \frac{{x + 36}}{{x - 36}}\end{array}\) Vậy \(B = \frac{{x + 36}}{{x - 36}}\) với \(x \ge 0;x \ne 36\). +) Thay \(x = 6\) (TMĐK) vào B, ta được: \(B = \frac{{42}}{{6 - 36}} = \frac{{42}}{{ - 30}} = - \frac{7}{5}\) Vậy \(B = - \frac{7}{5}\) khi \(x = 6\). Câu 3 (1,5 điểm). Cho hàm số \(y = \frac{2}{3}{x^2}\). a) Tìm hệ số a của \({x^2}\). b) Vẽ đồ thị của hàm số đã cho. Lời giải: a) Hệ số a của \({x^2}\) là \(a = \frac{2}{3}\). b) Ta có bảng giá trị sau:
Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 2;\frac{8}{3}} \right);\,\,B\left( { - 1;\frac{2}{3}} \right);C\left( {1;\frac{2}{3}} \right);\,\,D\left( {2;\frac{8}{3}} \right)\) Ta vẽ được đồ thị hàm số \(y = \frac{2}{3}{x^2}\) như sau:
Câu 4 (1,5 điểm). Cho phương trình bậc hai \(2{x^2} + 3x - 2 = 0\) a) Xác định các hệ số \(a,b,c\) của phương trình. b) Giải phương trình đã cho. Lời giải: a) Phương trình \(2{x^2} + 3x - 2 = 0\) có \(a = 2;b = 3;c = - 2.\) b) Ta có \(\Delta = {b^2} - 4ac = 9 - 4.2.\left( { - 2} \right) = 25 > 0\) Phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}} = \frac{{ - 3 + 5}}{{2.2}} = \frac{1}{2}\) và \(x_2^{} = \frac{{ - b - \sqrt \Delta }}{{2a}} = \frac{{ - 3 - 5}}{{2.2}} = - 2\). Vậy phương trình có hai nghiệm \(x \in \left\{ {\frac{1}{2}; - 2} \right\}.\) Câu 5 (1,0 điểm). Gieo đồng thời hai con xúc xắc cân đối và đồng chất. Tính xác suất của biến cố A: “Tổng số chấm xuất hiện trên hai mặt con xúc xắc bằng 5”.
Lời giải: Gieo đồng thời hai con con xúc xắc có 36 kết quả có thể xảy ra. Biến cố A: “Tổng số chấm xuất hiện trên hai mặt con xúc xắc bằng 5” Ta có \(A = \left\{ {(1;4),(2;3),(3;2),(4;1)} \right\}\), suy ra có 4 kết quả có thể xảy ra biến cố A. Xác suất của biến cố \(A\) là \(\frac{4}{{36}} = \frac{1}{9}.\) Câu 6 (1,0 điểm). Để chuẩn bị khen thưởng cho học sinh cuối năm học, Trường THCS X cần mua 1400 quyển vở và 700 cây bút ở Nhà sách Y để làm phần thưởng. Nhà trường dự tính mua với giá niêm yết sẽ cần 22 triệu 400 nghìn đồng, nhưng do mua với số lượng lớn nên Nhà sách Y đã giảm giá \(5{\rm{\% }}\) cho mỗi quyển vở và \(10{\rm{\% }}\) cho mỗi cây bút, vì thế nhà trường chỉ cần trả 21 triệu đồng. Tính giá tiền niêm yết của mỗi quyển vở và mỗi cây bút. Lời giải: Gọi giá niêm yết của mỗi quyển vở và mỗi cây bút lần lượt là \(x\),\(y\) (đồng, \(0 < x,y < 22400000\)) Nhà trường dự tính mua 1400 quyển vở và 700 cây bút với giá niêm yết sẽ cần 22 triệu 400 nghìn đồng nên ta có phương trình \(1400x + 700y = 22400000\) hay \(2x + y = 32000\) (1) Nhà sách Y đã giảm giá \(5{\rm{\% }}\) cho mỗi quyển vở và \(10{\rm{\% }}\) cho mỗi cây bút, vì thế nhà trường chỉ cần trả 21 triệu đồng nên ta có phương trình: \(1400x.(100\% - 5\% ) + 700y.(100\% - 10\% ) = 21000000\) hay \(19x + 9y = 300000\) (2) Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}2x + y = 32000\\19x + 9y = 300000\end{array} \right.\) \(\left\{ \begin{array}{l}18x + 9y = 288000\\19x + 9y = 300000\end{array} \right.\) \(\left\{ \begin{array}{l}x = 12000\\19x + 9y = 300000\end{array} \right.\) \(\left\{ \begin{array}{l}x = 12000\\y = 8000\end{array} \right.\,\,(tm)\) Vậy giá niêm yết của mỗi quyển vở là 12000 (đồng) và mỗi cây bút là 8000 (đồng). Câu 7 (0,5 điểm). Một tam giác vuông có cạnh huyền dài 13cm và diện tích bằng \(30{m^2}\). Lập phương trình bạc hai một ẩn có hai nghiệm là độ dài hai cạnh góc vuông của tam giác đã cho. Lời giải: Gọi độ dài hai cạnh góc vuông lần lượt là \(x,y{\rm{ cm}},\)\(0 < x,y < 13\). Đổi \(30{m^2} = 300000\,c{m^2}\) Diện tích tam giác là \(300000c{m^2}\) suy ra \(\begin{array}{l}\frac{1}{2}x.y = 300000\\xy = 600000\end{array}\) Vì cạnh huyền là 13 cm nên theo định lý Pythagore, ta có \(\begin{array}{l}{x^2} + {y^2} = {13^2} = 169\\{\left( {x + y} \right)^2} - 2xy = 169\\{\left( {x + y} \right)^2} - 1200000 = 169\\{\left( {x + y} \right)^2} = 1200169\end{array}\) Suy ra \(x + y = \sqrt {1200169} \) Vậy phương trình cần tìm là \({x^2} - \sqrt {1200169} x + 600000 = 0\) Đây là lời giải của HocTot.XYZ theo đúng đề bài gốc của tỉnh Bạc Liêu. Tuy nhiên phương trình tìm được là phương trình vô nghiệm. Câu 8 (2,5 điểm). Cho đường tròn (O; R) có đường kính AB vuông góc với dây cung CD tại điểm I (I nằm giữa A và O). Lấy điểm E bất kỳ trên cung nhỏ BC (E khác B và C). Hai đoạn thẳng AE và CD cắt nhau tại K. a) Chứng minh tứ giác KEBI là tứ giác nội tiếp. b) Chứng minh: \(AK \cdot AE = AB \cdot AI\). c) Gọi P là giao điểm cùa tia BE và tia DC, Q là giao điểm của hai đường thẳng AP và BK. Chứng minh OQ là tiếp tuyến của đường tròn ngoại tiếp \(\Delta PQE\). Lời giải:
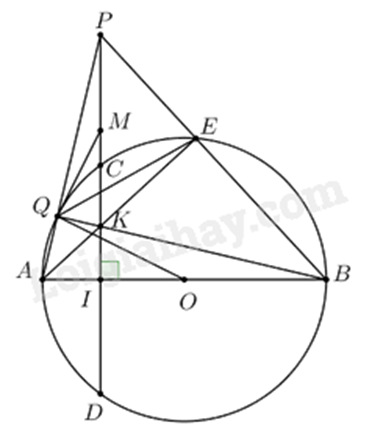
a) Do \(\widehat {AEB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) Nên \(\Delta KEB\) vuông tại E. Khi đó K, E, B cùng thuộc đường tròn đường kính KB Tương tự \(\Delta KIB\) vuông tại I nên K, I, B cùng thuộc đường tròn đường kính KB Suy ra K, E, B, I cùng thuộc đường tròn đường kính KB. Vậy tứ giác KEBI là tứ giác nội tiếp. b) Xét \(\Delta AKI\) và \(\Delta ABE\) có \(\widehat {BAE}\) là góc chung \(\widehat {AIK} = \widehat {AEB}\left( { = 90^\circ } \right)\) Suy ra $\Delta AKI\backsim \Delta ABE\left( g.g \right)$ Khi đó \(\frac{{AK}}{{AB}} = \frac{{AI}}{{AE}}\) (cặp cạnh tương ứng) hay \(AE.AK = AI.AB\) (đpcm) c) Xét \(\Delta ABP\) có \(AE \bot PB;PI \bot AB,\) AE và PI cắt nhau tại K nên K là trực tâm của \(\Delta ABP\) Suy ra \(BK \bot AP\) tại Q (Tính chất đồng quy của 3 đường cao) Khi đó \(\Delta PQK\) vuông tại Q nên P, Q, K cùng thuộc đường tròn đường kính PK Tương tự \(\Delta PEK\) vuông tại E nên P, E, K cùng thuộc đường tròn đường kính PK Vậy P, Q, K, E cùng thuộc đường tròn đường kính PK. Gọi M là trung điểm của PK. Khi đó M là tâm đường tròn ngoại tiếp \(\Delta PEQ\) Ta có \(MP = MQ\) nên \(\Delta MPQ\) cân tại M nên \(\widehat {MQP} = \widehat {MPQ}\) (1) Do \(BQ \bot AQ\left( {cmt} \right)\) nên \(\Delta ABQ\) vuông tại Q, trung tuyến OQ nên \(OQ = OA = OB\) Suy ra \(\Delta OAQ\) cân tại O nên \(\widehat {OQA} = \widehat {OAQ}\) (2) Từ (1) và (2) suy ra \(\widehat {MQP} + \widehat {OQA} = \widehat {MPQ} + \widehat {OAQ} = 90^\circ \) (do \(\Delta API\) vuông tại I) Suy ra \(\widehat {OQM} = 180^\circ - \left( {\widehat {MQP} + \widehat {OQA}} \right) = 180^\circ - 90^\circ = 90^\circ \) Suy ra \(OQ \bot MQ\) tại \(Q \in \left( M \right)\) Vậy OQ là tiếp tuyến của đường tròn ngoại tiếp \(\Delta PQE\).
|